ODE-Inspired Analysis for the Biological Version of Oja's Rule in Solving Streaming PCA
Paper and Code
Nov 04, 2019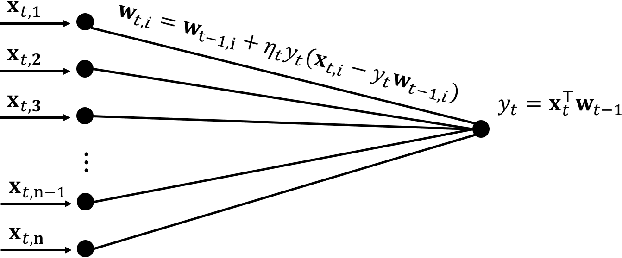
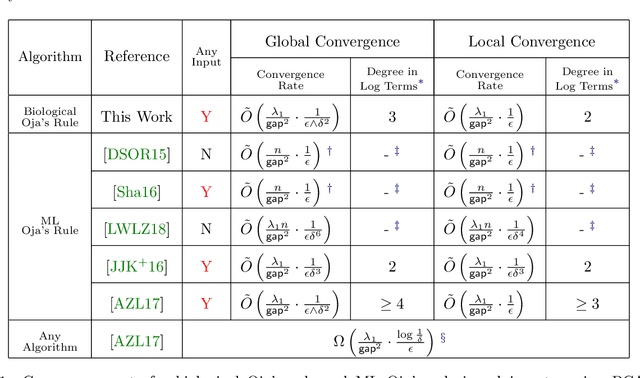
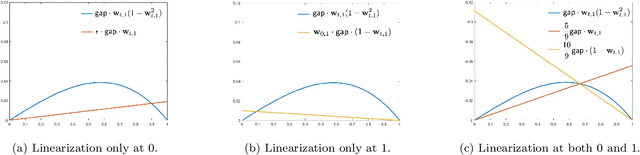
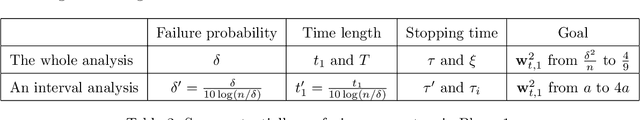
Oja's rule [Oja, Journal of mathematical biology 1982] is a well-known biologically-plausible algorithm using a Hebbian-type synaptic update rule to solve streaming principal component analysis (PCA). Computational neuroscientists have known that this biological version of Oja's rule converges to the top eigenvector of the covariance matrix of the input in the limit. However, prior to this work, it was open to prove any convergence rate guarantee. In this work, we give the first convergence rate analysis for the biological version of Oja's rule in solving streaming PCA. Moreover, our convergence rate matches the information theoretical lower bound up to logarithmic factors and outperforms the state-of-the-art upper bound for streaming PCA. Furthermore, we develop a novel framework inspired by ordinary differential equations (ODE) to analyze general stochastic dynamics. The framework abandons the traditional step-by-step analysis and instead analyzes a stochastic dynamic in one-shot by giving a closed-form solution to the entire dynamic. The one-shot framework allows us to apply stopping time and martingale techniques to have a flexible and precise control on the dynamic. We believe that this general framework is powerful and should lead to effective yet simple analysis for a large class of problems with stochastic dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge