Mien Brabeeba Wang
A General Framework for Analyzing Stochastic Dynamics in Learning Algorithms
Jun 11, 2020
Abstract:We present a general framework for analyzing high-probability bounds for stochastic dynamics in learning algorithms. Our framework composes standard techniques such as a stopping time, a martingale concentration and a closed-from solution to give a streamlined three-step recipe with a general and flexible principle to implement it. To demonstrate the power and the flexibility of our framework, we apply the framework on three very different learning problems: stochastic gradient descent for strongly convex functions, streaming principal component analysis and linear bandit with stochastic gradient descent updates. We improve the state of the art bounds on all three dynamics.
ODE-Inspired Analysis for the Biological Version of Oja's Rule in Solving Streaming PCA
Nov 04, 2019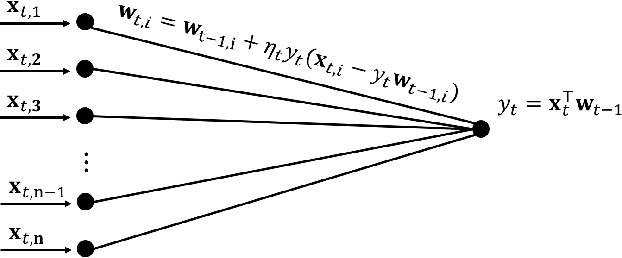
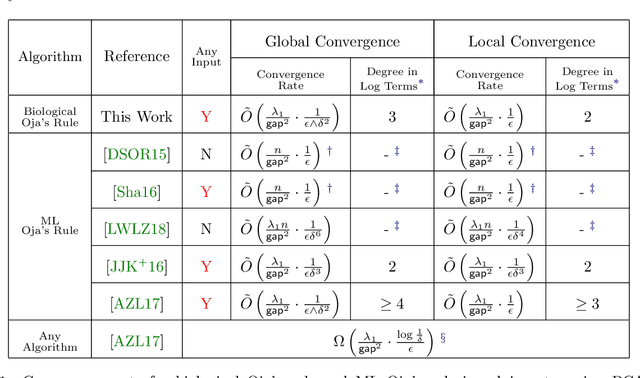
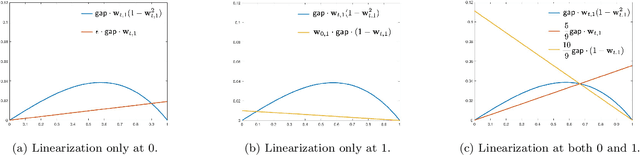
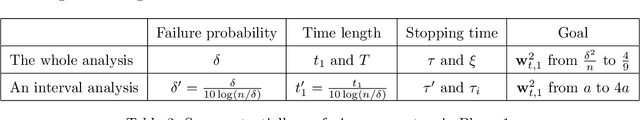
Abstract:Oja's rule [Oja, Journal of mathematical biology 1982] is a well-known biologically-plausible algorithm using a Hebbian-type synaptic update rule to solve streaming principal component analysis (PCA). Computational neuroscientists have known that this biological version of Oja's rule converges to the top eigenvector of the covariance matrix of the input in the limit. However, prior to this work, it was open to prove any convergence rate guarantee. In this work, we give the first convergence rate analysis for the biological version of Oja's rule in solving streaming PCA. Moreover, our convergence rate matches the information theoretical lower bound up to logarithmic factors and outperforms the state-of-the-art upper bound for streaming PCA. Furthermore, we develop a novel framework inspired by ordinary differential equations (ODE) to analyze general stochastic dynamics. The framework abandons the traditional step-by-step analysis and instead analyzes a stochastic dynamic in one-shot by giving a closed-form solution to the entire dynamic. The one-shot framework allows us to apply stopping time and martingale techniques to have a flexible and precise control on the dynamic. We believe that this general framework is powerful and should lead to effective yet simple analysis for a large class of problems with stochastic dynamics.
Integrating Temporal Information to Spatial Information in a Neural Circuit
Mar 01, 2019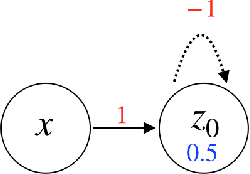
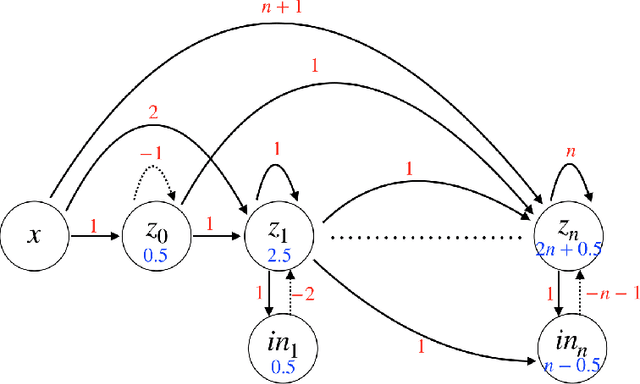
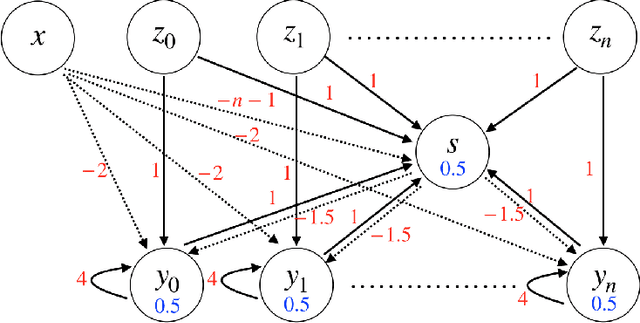
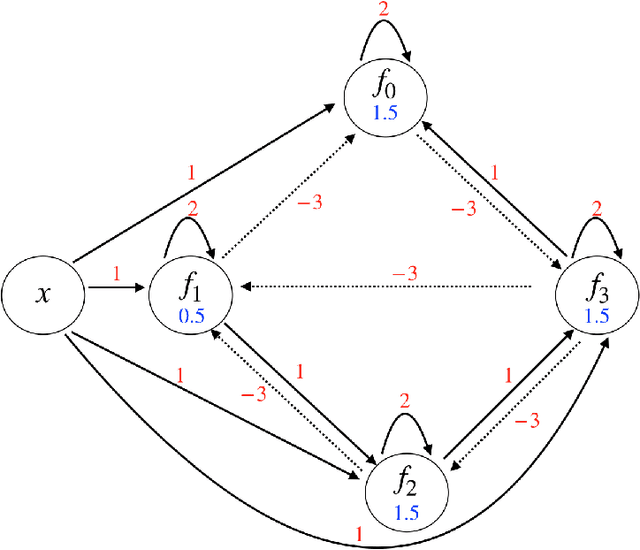
Abstract:In this paper, we consider a network of spiking neurons with a deterministic synchronous firing rule at discrete time. We propose three problems -- "first consecutive spikes counting", "total spikes counting" and "$k$-spikes temporal to spatial encoding" -- to model how brains extract temporal information into spatial information from different neural codings. For a max input length $T$, we design three networks that solve these three problems with matching lower bounds in both time $O(T)$ and number of neurons $O(\log T)$ in all three questions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge