Integrating Temporal Information to Spatial Information in a Neural Circuit

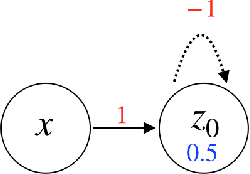
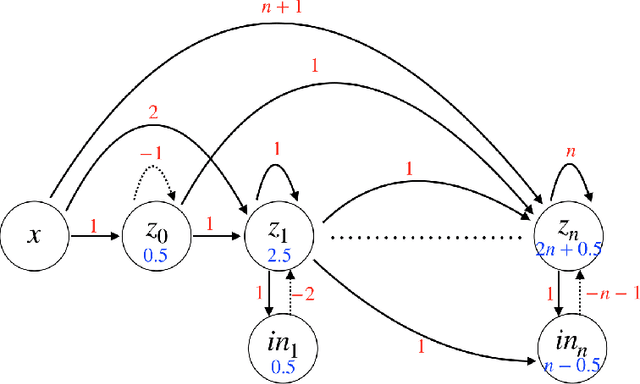
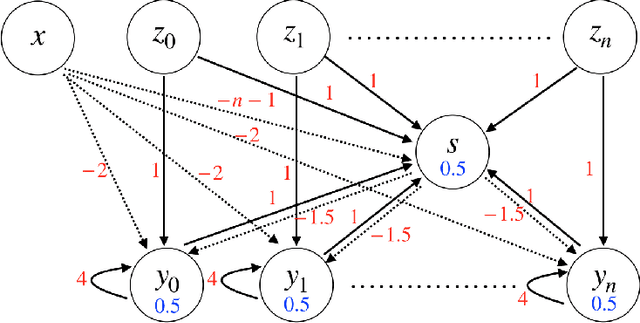
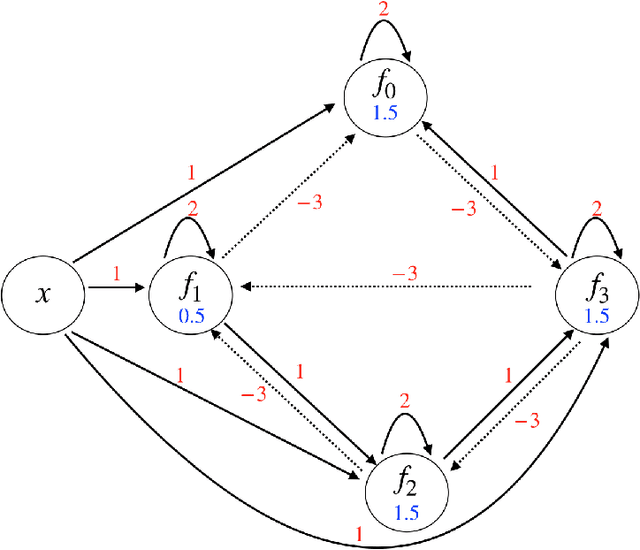
In this paper, we consider a network of spiking neurons with a deterministic synchronous firing rule at discrete time. We propose three problems -- "first consecutive spikes counting", "total spikes counting" and "$k$-spikes temporal to spatial encoding" -- to model how brains extract temporal information into spatial information from different neural codings. For a max input length $T$, we design three networks that solve these three problems with matching lower bounds in both time $O(T)$ and number of neurons $O(\log T)$ in all three questions.