Improved analysis of randomized SVD for top-eigenvector approximation

Computing the top eigenvectors of a matrix is a problem of fundamental interest to various fields. While the majority of the literature has focused on analyzing the reconstruction error of low-rank matrices associated with the retrieved eigenvectors, in many applications one is interested in finding one vector with high Rayleigh quotient. In this paper we study the problem of approximating the top-eigenvector. Given a symmetric matrix $\mathbf{A}$ with largest eigenvalue $\lambda_1$, our goal is to find a vector \hu that approximates the leading eigenvector $\mathbf{u}_1$ with high accuracy, as measured by the ratio $R(\hat{\mathbf{u}})=\lambda_1^{-1}{\hat{\mathbf{u}}^T\mathbf{A}\hat{\mathbf{u}}}/{\hat{\mathbf{u}}^T\hat{\mathbf{u}}}$. We present a novel analysis of the randomized SVD algorithm of \citet{halko2011finding} and derive tight bounds in many cases of interest. Notably, this is the first work that provides non-trivial bounds of $R(\hat{\mathbf{u}})$ for randomized SVD with any number of iterations. Our theoretical analysis is complemented with a thorough experimental study that confirms the efficiency and accuracy of the method.

Rethinking Why Intermediate-Task Fine-Tuning Works

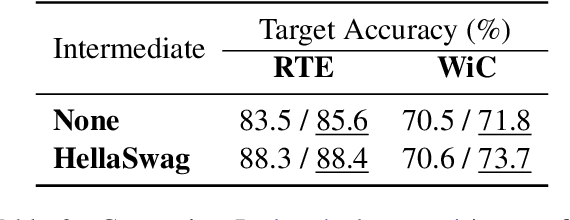
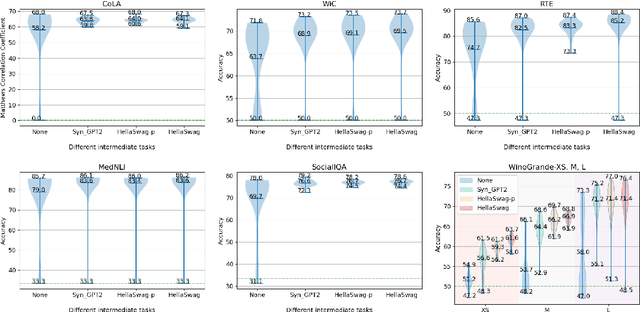
Supplementary Training on Intermediate Labeled-data Tasks (STILTs) is a widely applied technique, which first fine-tunes the pretrained language models on an intermediate task before on the target task of interest. While STILTs is able to further improve the performance of pretrained language models, it is still unclear why and when it works. Previous research shows that those intermediate tasks involving complex inference, such as commonsense reasoning, work especially well for RoBERTa. In this paper, we discover that the improvement from an intermediate task could be orthogonal to it containing reasoning or other complex skills -- a simple real-fake discrimination task synthesized by GPT2 can benefit diverse target tasks. We conduct extensive experiments to study the impact of different factors on STILTs. These findings suggest rethinking the role of intermediate fine-tuning in the STILTs pipeline.

TinyGAN: Distilling BigGAN for Conditional Image Generation

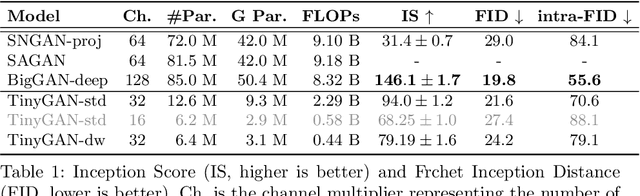
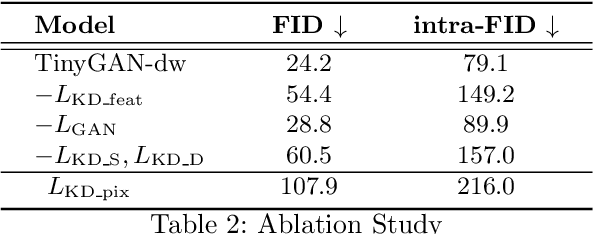
Generative Adversarial Networks (GANs) have become a powerful approach for generative image modeling. However, GANs are notorious for their training instability, especially on large-scale, complex datasets. While the recent work of BigGAN has significantly improved the quality of image generation on ImageNet, it requires a huge model, making it hard to deploy on resource-constrained devices. To reduce the model size, we propose a black-box knowledge distillation framework for compressing GANs, which highlights a stable and efficient training process. Given BigGAN as the teacher network, we manage to train a much smaller student network to mimic its functionality, achieving competitive performance on Inception and FID scores with the generator having $16\times$ fewer parameters.

On the Algorithmic Power of Spiking Neural Networks

Spiking Neural Networks (SNN) are mathematical models in neuroscience to describe the dynamics among a set of neurons which interact with each other by firing spike signals to each other. Interestingly, recent works observed that for an integrate-and-fire model, when configured appropriately (e.g., after the parameters are learned properly), the neurons' firing rate, i.e., converges to an optimal solution of Lasso and certain quadratic optimization problems. Thus, SNN can be viewed as a natural algorithm for solving such convex optimization problems. However, theoretical understanding of SNN algorithms remains limited. In particular, only the convergence result for the Lasso problem is known, but the bounds of the convergence rate remain unknown. Therefore, we do not know any explicit complexity bounds for SNN algorithms. In this work, we investigate the algorithmic power of the integrate-and-fire SNN model after the parameters are properly learned/configured. In particular, we explore what algorithms SNN can implement. We start by formulating a clean discrete-time SNN model to facilitate the algorithmic study. We consider two SNN dynamics and obtain the following results. * We first consider an arguably simplest SNN dynamics with a threshold spiking rule, which we call simple SNN. We show that simple SNN solves the least square problem for a matrix $A\in\mathbb{R}^{m\times n}$ and vector $\mathbf{b} \in \mathbb{R}^m$ with timestep complexity $O(\kappa n/\epsilon)$. * For the under-determined case, we observe that simple SNN may solve the $\ell_1$ minimization problem using an interesting primal-dual algorithm, which solves the dual problem by a gradient-based algorithm while updates the primal solution along the way. We analyze a variant dynamics and use simulation to serve as partial evidence to support the conjecture.

Online Reinforcement Learning in Stochastic Games

We study online reinforcement learning in average-reward stochastic games (SGs). An SG models a two-player zero-sum game in a Markov environment, where state transitions and one-step payoffs are determined simultaneously by a learner and an adversary. We propose the UCSG algorithm that achieves a sublinear regret compared to the game value when competing with an arbitrary opponent. This result improves previous ones under the same setting. The regret bound has a dependency on the diameter, which is an intrinsic value related to the mixing property of SGs. If we let the opponent play an optimistic best response to the learner, UCSG finds an $\varepsilon$-maximin stationary policy with a sample complexity of $\tilde{\mathcal{O}}\left(\text{poly}(1/\varepsilon)\right)$, where $\varepsilon$ is the gap to the best policy.

Tracking the Best Expert in Non-stationary Stochastic Environments

We study the dynamic regret of multi-armed bandit and experts problem in non-stationary stochastic environments. We introduce a new parameter $\Lambda$, which measures the total statistical variance of the loss distributions over $T$ rounds of the process, and study how this amount affects the regret. We investigate the interaction between $\Lambda$ and $\Gamma$, which counts the number of times the distributions change, as well as $\Lambda$ and $V$, which measures how far the distributions deviates over time. One striking result we find is that even when $\Gamma$, $V$, and $\Lambda$ are all restricted to constant, the regret lower bound in the bandit setting still grows with $T$. The other highlight is that in the full-information setting, a constant regret becomes achievable with constant $\Gamma$ and $\Lambda$, as it can be made independent of $T$, while with constant $V$ and $\Lambda$, the regret still has a $T^{1/3}$ dependency. We not only propose algorithms with upper bound guarantee, but prove their matching lower bounds as well.

Generalized Mirror Descents in Congestion Games

Different types of dynamics have been studied in repeated game play, and one of them which has received much attention recently consists of those based on "no-regret" algorithms from the area of machine learning. It is known that dynamics based on generic no-regret algorithms may not converge to Nash equilibria in general, but to a larger set of outcomes, namely coarse correlated equilibria. Moreover, convergence results based on generic no-regret algorithms typically use a weaker notion of convergence: the convergence of the average plays instead of the actual plays. Some work has been done showing that when using a specific no-regret algorithm, the well-known multiplicative updates algorithm, convergence of actual plays to equilibria can be shown and better quality of outcomes in terms of the price of anarchy can be reached for atomic congestion games and load balancing games. Are there more cases of natural no-regret dynamics that perform well in suitable classes of games in terms of convergence and quality of outcomes that the dynamics converge to? We answer this question positively in the bulletin-board model by showing that when employing the mirror-descent algorithm, a well-known generic no-regret algorithm, the actual plays converge quickly to equilibria in nonatomic congestion games. Furthermore, the bandit model considers a probably more realistic and prevalent setting with only partial information, in which at each time step each player only knows the cost of her own currently played strategy, but not any costs of unplayed strategies. For the class of atomic congestion games, we propose a family of bandit algorithms based on the mirror-descent algorithms previously presented, and show that when each player individually adopts such a bandit algorithm, their joint (mixed) strategy profile quickly converges with implications.

Rivalry of Two Families of Algorithms for Memory-Restricted Streaming PCA

We study the problem of recovering the subspace spanned by the first $k$ principal components of $d$-dimensional data under the streaming setting, with a memory bound of $O(kd)$. Two families of algorithms are known for this problem. The first family is based on the framework of stochastic gradient descent. Nevertheless, the convergence rate of the family can be seriously affected by the learning rate of the descent steps and deserves more serious study. The second family is based on the power method over blocks of data, but setting the block size for its existing algorithms is not an easy task. In this paper, we analyze the convergence rate of a representative algorithm with decayed learning rate (Oja and Karhunen, 1985) in the first family for the general $k>1$ case. Moreover, we propose a novel algorithm for the second family that sets the block sizes automatically and dynamically with faster convergence rate. We then conduct empirical studies that fairly compare the two families on real-world data. The studies reveal the advantages and disadvantages of these two families.

An Online Boosting Algorithm with Theoretical Justifications

We study the task of online boosting--combining online weak learners into an online strong learner. While batch boosting has a sound theoretical foundation, online boosting deserves more study from the theoretical perspective. In this paper, we carefully compare the differences between online and batch boosting, and propose a novel and reasonable assumption for the online weak learner. Based on the assumption, we design an online boosting algorithm with a strong theoretical guarantee by adapting from the offline SmoothBoost algorithm that matches the assumption closely. We further tackle the task of deciding the number of weak learners using established theoretical results for online convex programming and predicting with expert advice. Experiments on real-world data sets demonstrate that the proposed algorithm compares favorably with existing online boosting algorithms.