Multilayer Correlation Clustering

In this paper, we establish Multilayer Correlation Clustering, a novel generalization of Correlation Clustering (Bansal et al., FOCS '02) to the multilayer setting. In this model, we are given a series of inputs of Correlation Clustering (called layers) over the common set $V$. The goal is then to find a clustering of $V$ that minimizes the $\ell_p$-norm ($p\geq 1$) of the disagreements vector, which is defined as the vector (with dimension equal to the number of layers), each element of which represents the disagreements of the clustering on the corresponding layer. For this generalization, we first design an $O(L\log n)$-approximation algorithm, where $L$ is the number of layers, based on the well-known region growing technique. We then study an important special case of our problem, namely the problem with the probability constraint. For this case, we first give an $(\alpha+2)$-approximation algorithm, where $\alpha$ is any possible approximation ratio for the single-layer counterpart. For instance, we can take $\alpha=2.5$ in general (Ailon et al., JACM '08) and $\alpha=1.73+\epsilon$ for the unweighted case (Cohen-Addad et al., FOCS '23). Furthermore, we design a $4$-approximation algorithm, which improves the above approximation ratio of $\alpha+2=4.5$ for the general probability-constraint case. Computational experiments using real-world datasets demonstrate the effectiveness of our proposed algorithms.

Improved analysis of randomized SVD for top-eigenvector approximation

Computing the top eigenvectors of a matrix is a problem of fundamental interest to various fields. While the majority of the literature has focused on analyzing the reconstruction error of low-rank matrices associated with the retrieved eigenvectors, in many applications one is interested in finding one vector with high Rayleigh quotient. In this paper we study the problem of approximating the top-eigenvector. Given a symmetric matrix $\mathbf{A}$ with largest eigenvalue $\lambda_1$, our goal is to find a vector \hu that approximates the leading eigenvector $\mathbf{u}_1$ with high accuracy, as measured by the ratio $R(\hat{\mathbf{u}})=\lambda_1^{-1}{\hat{\mathbf{u}}^T\mathbf{A}\hat{\mathbf{u}}}/{\hat{\mathbf{u}}^T\hat{\mathbf{u}}}$. We present a novel analysis of the randomized SVD algorithm of \citet{halko2011finding} and derive tight bounds in many cases of interest. Notably, this is the first work that provides non-trivial bounds of $R(\hat{\mathbf{u}})$ for randomized SVD with any number of iterations. Our theoretical analysis is complemented with a thorough experimental study that confirms the efficiency and accuracy of the method.

Scalable Dyadic Independence Models with Local and Global Constraints

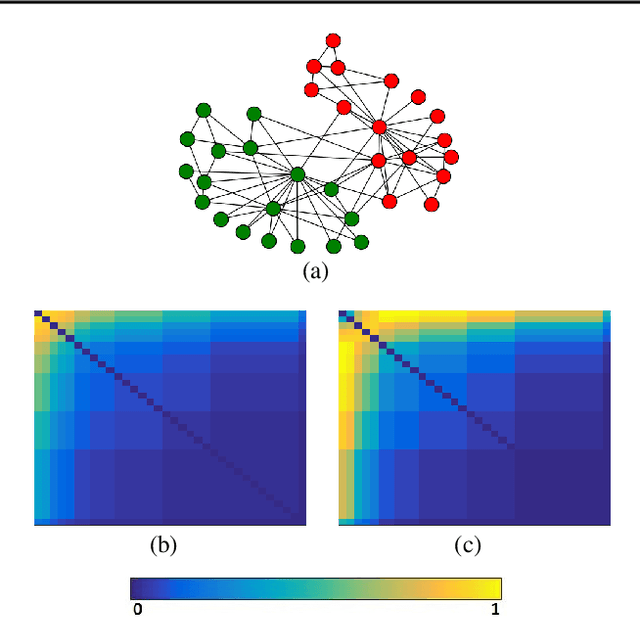
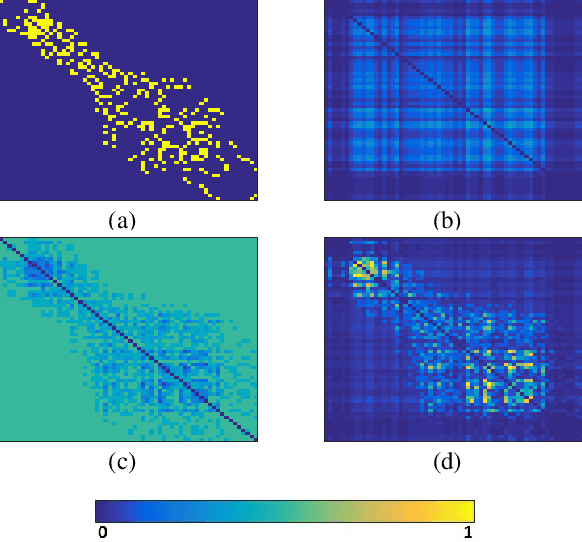
An important challenge in the field of exponential random graphs (ERGs) is the fitting of non-trivial ERGs on large networks. By utilizing matrix block-approximation techniques, we propose an approximative framework to such non-trivial ERGs that result in dyadic independence (i.e., edge independent) models, while being able to meaningfully model local information (degrees) as well as global information (clustering coefficient, assortativity, etc.) if desired. This allows one to efficiently generate random networks with similar properties as an observed network, scalable up to sparse graphs consisting of millions of nodes. Empirical evaluation demonstrates its competitiveness in terms of accuracy with state-of-the-art methods for link prediction and network reconstruction.