Approximating splits for decision trees quickly in sparse data streams

Decision trees are one of the most popular classifiers in the machine learning literature. While the most common decision tree learning algorithms treat data as a batch, numerous algorithms have been proposed to construct decision trees from a data stream. A standard training strategy involves augmenting the current tree by changing a leaf node into a split. Here we typically maintain counters in each leaf which allow us to determine the optimal split, and whether the split should be done. In this paper we focus on how to speed up the search for the optimal split when dealing with sparse binary features and a binary class. We focus on finding splits that have the approximately optimal information gain or Gini index. In both cases finding the optimal split can be done in $O(d)$ time, where $d$ is the number of features. We propose an algorithm that yields $(1 + α)$ approximation when using conditional entropy in amortized $O(α^{-1}(1 + m\log d) \log \log n)$ time, where $m$ is the number of 1s in a data point, and $n$ is the number of data points. Similarly, for Gini index, we achieve $(1 + α)$ approximation in amortized $O(α^{-1} + m \log d)$ time. Our approach is beneficial for sparse data where $m \ll d$. In our experiments we find almost-optimal splits efficiently, faster than the baseline, overperforming the theoretical approximation guarantees.

Multilayer Correlation Clustering

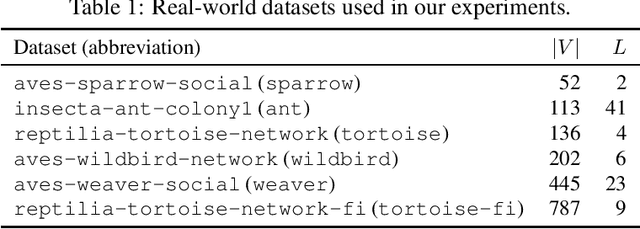
In this paper, we establish Multilayer Correlation Clustering, a novel generalization of Correlation Clustering (Bansal et al., FOCS '02) to the multilayer setting. In this model, we are given a series of inputs of Correlation Clustering (called layers) over the common set $V$. The goal is then to find a clustering of $V$ that minimizes the $\ell_p$-norm ($p\geq 1$) of the disagreements vector, which is defined as the vector (with dimension equal to the number of layers), each element of which represents the disagreements of the clustering on the corresponding layer. For this generalization, we first design an $O(L\log n)$-approximation algorithm, where $L$ is the number of layers, based on the well-known region growing technique. We then study an important special case of our problem, namely the problem with the probability constraint. For this case, we first give an $(\alpha+2)$-approximation algorithm, where $\alpha$ is any possible approximation ratio for the single-layer counterpart. For instance, we can take $\alpha=2.5$ in general (Ailon et al., JACM '08) and $\alpha=1.73+\epsilon$ for the unweighted case (Cohen-Addad et al., FOCS '23). Furthermore, we design a $4$-approximation algorithm, which improves the above approximation ratio of $\alpha+2=4.5$ for the general probability-constraint case. Computational experiments using real-world datasets demonstrate the effectiveness of our proposed algorithms.

Jaccard-constrained dense subgraph discovery

Finding dense subgraphs is a core problem in graph mining with many applications in diverse domains. At the same time many real-world networks vary over time, that is, the dataset can be represented as a sequence of graph snapshots. Hence, it is natural to consider the question of finding dense subgraphs in a temporal network that are allowed to vary over time to a certain degree. In this paper, we search for dense subgraphs that have large pairwise Jaccard similarity coefficients. More formally, given a set of graph snapshots and a weight $\lambda$, we find a collection of dense subgraphs such that the sum of densities of the induced subgraphs plus the sum of Jaccard indices, weighted by $\lambda$, is maximized. We prove that this problem is NP-hard. To discover dense subgraphs with good objective value, we present an iterative algorithm which runs in $\mathcal{O}(n^2k^2 + m \log n + k^3 n)$ time per single iteration, and a greedy algorithm which runs in $\mathcal{O}(n^2k^2 + m \log n + k^3 n)$ time, where $k$ is the length of the graph sequence and $n$ and $m$ denote number of nodes and total number of edges respectively. We show experimentally that our algorithms are efficient, they can find ground truth in synthetic datasets and provide interpretable results from real-world datasets. Finally, we present a case study that shows the usefulness of our problem.

Fast likelihood-based change point detection

Change point detection plays a fundamental role in many real-world applications, where the goal is to analyze and monitor the behaviour of a data stream. In this paper, we study change detection in binary streams. To this end, we use a likelihood ratio between two models as a measure for indicating change. The first model is a single bernoulli variable while the second model divides the stored data in two segments, and models each segment with its own bernoulli variable. Finding the optimal split can be done in $O(n)$ time, where $n$ is the number of entries since the last change point. This is too expensive for large $n$. To combat this we propose an approximation scheme that yields $(1 - \epsilon)$ approximation in $O(\epsilon^{-1} \log^2 n)$ time. The speed-up consists of several steps: First we reduce the number of possible candidates by adopting a known result from segmentation problems. We then show that for fixed bernoulli parameters we can find the optimal change point in logarithmic time. Finally, we show how to construct a candidate list of size $O(\epsilon^{-1} \log n)$ for model parameters. We demonstrate empirically the approximation quality and the running time of our algorithm, showing that we can gain a significant speed-up with a minimal average loss in optimality.

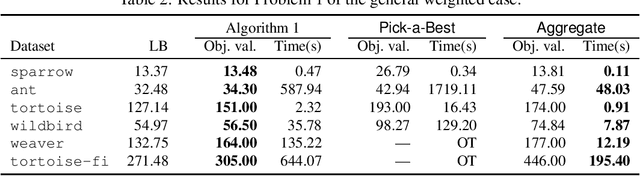
Recurrent segmentation meets block models in temporal networks

A popular approach to model interactions is to represent them as a network with nodes being the agents and the interactions being the edges. Interactions are often timestamped, which leads to having timestamped edges. Many real-world temporal networks have a recurrent or possibly cyclic behaviour. For example, social network activity may be heightened during certain hours of day. In this paper, our main interest is to model recurrent activity in such temporal networks. As a starting point we use stochastic block model, a popular choice for modelling static networks, where nodes are split into $R$ groups. We extend this model to temporal networks by modelling the edges with a Poisson process. We make the parameters of the process dependent on time by segmenting the time line into $K$ segments. To enforce the recurring activity we require that only $H < K$ different set of parameters can be used, that is, several, not necessarily consecutive, segments must share their parameters. We prove that the searching for optimal blocks and segmentation is an NP-hard problem. Consequently, we split the problem into 3 subproblems where we optimize blocks, model parameters, and segmentation in turn while keeping the remaining structures fixed. We propose an iterative algorithm that requires $O(KHm + Rn + R^2H)$ time per iteration, where $n$ and $m$ are the number of nodes and edges in the network. We demonstrate experimentally that the number of required iterations is typically low, the algorithm is able to discover the ground truth from synthetic datasets, and show that certain real-world networks exhibit recurrent behaviour as the likelihood does not deteriorate when $H$ is lowered.

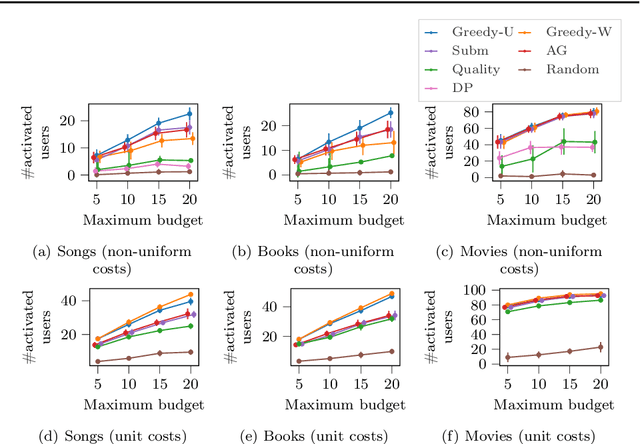
Ranking with submodular functions on a budget

Submodular maximization has been the backbone of many important machine-learning problems, and has applications to viral marketing, diversification, sensor placement, and more. However, the study of maximizing submodular functions has mainly been restricted in the context of selecting a set of items. On the other hand, many real-world applications require a solution that is a ranking over a set of items. The problem of ranking in the context of submodular function maximization has been considered before, but to a much lesser extent than item-selection formulations. In this paper, we explore a novel formulation for ranking items with submodular valuations and budget constraints. We refer to this problem as max-submodular ranking (MSR). In more detail, given a set of items and a set of non-decreasing submodular functions, where each function is associated with a budget, we aim to find a ranking of the set of items that maximizes the sum of values achieved by all functions under the budget constraints. For the MSR problem with cardinality- and knapsack-type budget constraints we propose practical algorithms with approximation guarantees. In addition, we perform an empirical evaluation, which demonstrates the superior performance of the proposed algorithms against strong baselines.

Approximation algorithms for confidence bands for time series

Confidence intervals are a standard technique for analyzing data. When applied to time series, confidence intervals are computed for each time point separately. Alternatively, we can compute confidence bands, where we are required to find the smallest area enveloping $k$ time series, where $k$ is a user parameter. Confidence bands can be then used to detect abnormal time series, not just individual observations within the time series. We will show that despite being an NP-hard problem it is possible to find optimal confidence band for some $k$. We do this by considering a different problem: discovering regularized bands, where we minimize the envelope area minus the number of included time series weighted by a parameter $\alpha$. Unlike normal confidence bands we can solve the problem exactly by using a minimum cut. By varying $\alpha$ we can obtain solutions for various $k$. If we have a constraint $k$ for which we cannot find appropriate $\alpha$, we demonstrate a simple algorithm that yields $O(\sqrt{n})$ approximation guarantee by connecting the problem to a minimum $k$-union problem. This connection also implies that we cannot approximate the problem better than $O(n^{1/4})$ under some (mild) assumptions. Finally, we consider a variant where instead of minimizing the area we minimize the maximum width. Here, we demonstrate a simple 2-approximation algorithm and show that we cannot achieve better approximation guarantee.

Maintaining AUC and $H$-measure over time

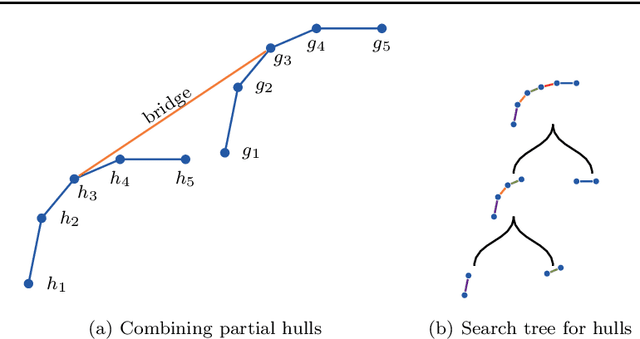
Measuring the performance of a classifier is a vital task in machine learning. The running time of an algorithm that computes the measure plays a very small role in an offline setting, for example, when the classifier is being developed by a researcher. However, the running time becomes more crucial if our goal is to monitor the performance of a classifier over time. In this paper we study three algorithms for maintaining two measures. The first algorithm maintains area under the ROC curve (AUC) under addition and deletion of data points in $O(\log n)$ time. This is done by maintaining the data points sorted in a self-balanced search tree. In addition, we augment the search tree that allows us to query the ROC coordinates of a data point in $O(\log n)$ time. In doing so we are able to maintain AUC in $O(\log n)$ time. Our next two algorithms involve in maintaining $H$-measure, an alternative measure based on the ROC curve. Computing the measure is a two-step process: first we need to compute a convex hull of the ROC curve, followed by a sum over the convex hull. We demonstrate that we can maintain the convex hull using a minor modification of the classic convex hull maintenance algorithm. We then show that under certain conditions, we can compute the $H$-measure exactly in $O(\log^2 n)$ time, and if the conditions are not met, then we can estimate the $H$-measure in $O((\log n + \epsilon^{-1})\log n)$ time. We show empirically that our methods are significantly faster than the baselines.

Decomposable Families of Itemsets

The problem of selecting a small, yet high quality subset of patterns from a larger collection of itemsets has recently attracted lot of research. Here we discuss an approach to this problem using the notion of decomposable families of itemsets. Such itemset families define a probabilistic model for the data from which the original collection of itemsets has been derived from. Furthermore, they induce a special tree structure, called a junction tree, familiar from the theory of Markov Random Fields. The method has several advantages. The junction trees provide an intuitive representation of the mining results. From the computational point of view, the model provides leverage for problems that could be intractable using the entire collection of itemsets. We provide an efficient algorithm to build decomposable itemset families, and give an application example with frequency bound querying using the model. Empirical results show that our algorithm yields high quality results.

Tell Me Something I Don't Know: Randomization Strategies for Iterative Data Mining

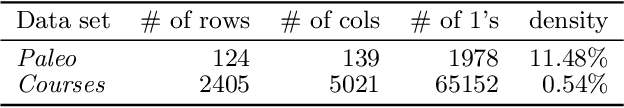
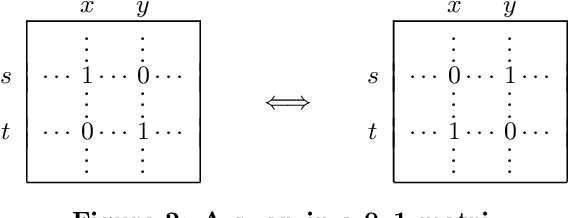
There is a wide variety of data mining methods available, and it is generally useful in exploratory data analysis to use many different methods for the same dataset. This, however, leads to the problem of whether the results found by one method are a reflection of the phenomenon shown by the results of another method, or whether the results depict in some sense unrelated properties of the data. For example, using clustering can give indication of a clear cluster structure, and computing correlations between variables can show that there are many significant correlations in the data. However, it can be the case that the correlations are actually determined by the cluster structure. In this paper, we consider the problem of randomizing data so that previously discovered patterns or models are taken into account. The randomization methods can be used in iterative data mining. At each step in the data mining process, the randomization produces random samples from the set of data matrices satisfying the already discovered patterns or models. That is, given a data set and some statistics (e.g., cluster centers or co-occurrence counts) of the data, the randomization methods sample data sets having similar values of the given statistics as the original data set. We use Metropolis sampling based on local swaps to achieve this. We describe experiments on real data that demonstrate the usefulness of our approach. Our results indicate that in many cases, the results of, e.g., clustering actually imply the results of, say, frequent pattern discovery.