Maximum Entropy Based Significance of Itemsets
Paper and Code
Apr 27, 2019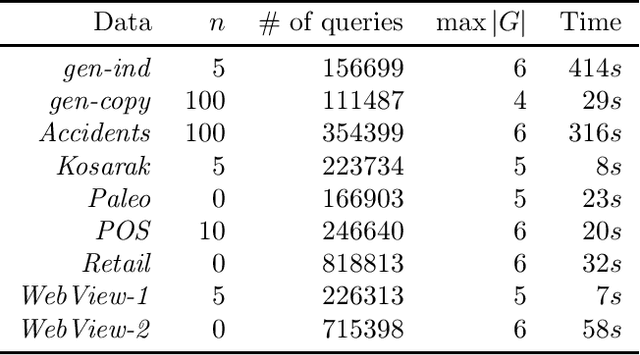

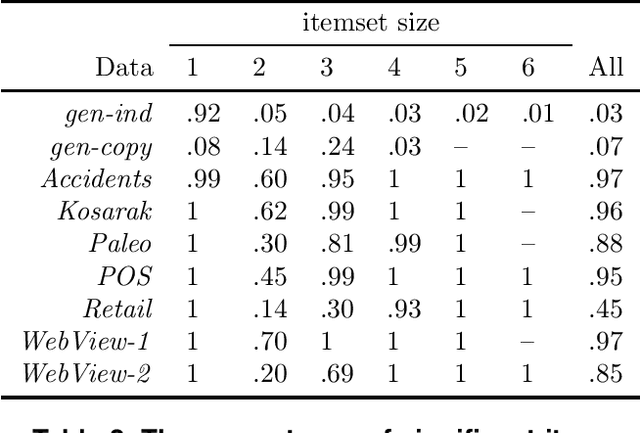
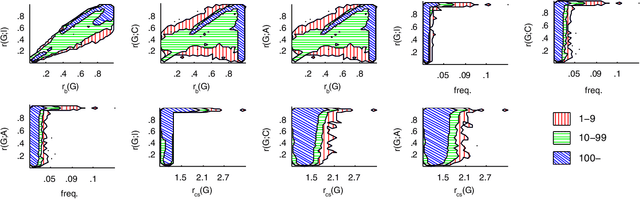
We consider the problem of defining the significance of an itemset. We say that the itemset is significant if we are surprised by its frequency when compared to the frequencies of its sub-itemsets. In other words, we estimate the frequency of the itemset from the frequencies of its sub-itemsets and compute the deviation between the real value and the estimate. For the estimation we use Maximum Entropy and for measuring the deviation we use Kullback-Leibler divergence. A major advantage compared to the previous methods is that we are able to use richer models whereas the previous approaches only measure the deviation from the independence model. We show that our measure of significance goes to zero for derivable itemsets and that we can use the rank as a statistical test. Our empirical results demonstrate that for our real datasets the independence assumption is too strong but applying more flexible models leads to good results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge