Multilayer Correlation Clustering
Paper and Code
Apr 25, 2024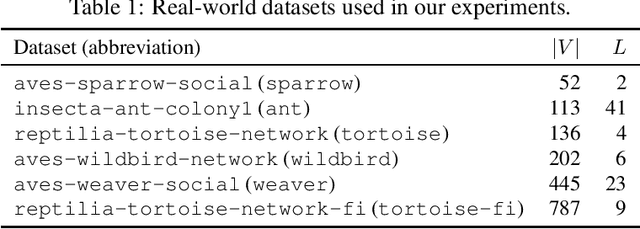
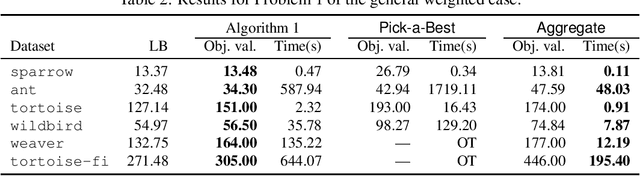

In this paper, we establish Multilayer Correlation Clustering, a novel generalization of Correlation Clustering (Bansal et al., FOCS '02) to the multilayer setting. In this model, we are given a series of inputs of Correlation Clustering (called layers) over the common set $V$. The goal is then to find a clustering of $V$ that minimizes the $\ell_p$-norm ($p\geq 1$) of the disagreements vector, which is defined as the vector (with dimension equal to the number of layers), each element of which represents the disagreements of the clustering on the corresponding layer. For this generalization, we first design an $O(L\log n)$-approximation algorithm, where $L$ is the number of layers, based on the well-known region growing technique. We then study an important special case of our problem, namely the problem with the probability constraint. For this case, we first give an $(\alpha+2)$-approximation algorithm, where $\alpha$ is any possible approximation ratio for the single-layer counterpart. For instance, we can take $\alpha=2.5$ in general (Ailon et al., JACM '08) and $\alpha=1.73+\epsilon$ for the unweighted case (Cohen-Addad et al., FOCS '23). Furthermore, we design a $4$-approximation algorithm, which improves the above approximation ratio of $\alpha+2=4.5$ for the general probability-constraint case. Computational experiments using real-world datasets demonstrate the effectiveness of our proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge