Heikki Mannila
Consistent Multigroup Low-Rank Approximation
Mar 27, 2025Abstract:We consider the problem of consistent low-rank approximation for multigroup data: we ask for a sequence of $k$ basis vectors such that projecting the data onto their spanned subspace treats all groups as equally as possible, by minimizing the maximum error among the groups. Additionally, we require that the sequence of basis vectors satisfies the natural consistency property: when looking for the best $k$ vectors, the first $d<k$ vectors are the best possible solution to the problem of finding $d$ basis vectors. Thus, this multigroup low-rank approximation method naturally generalizes \svd and reduces to \svd for data with a single group. We give an iterative algorithm for this task that sequentially adds to the basis the vector that gives the best rank$-1$ projection according to the min-max criterion, and then projects the data onto the orthogonal complement of that vector. For finding the best rank$-1$ projection, we use primal-dual approaches or semidefinite programming. We analyze the theoretical properties of the algorithms and demonstrate empirically that the proposed methods compare favorably to existing methods for multigroup (or fair) PCA.
Tell Me Something I Don't Know: Randomization Strategies for Iterative Data Mining
Jun 16, 2020
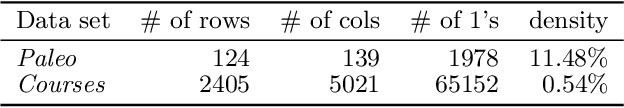

Abstract:There is a wide variety of data mining methods available, and it is generally useful in exploratory data analysis to use many different methods for the same dataset. This, however, leads to the problem of whether the results found by one method are a reflection of the phenomenon shown by the results of another method, or whether the results depict in some sense unrelated properties of the data. For example, using clustering can give indication of a clear cluster structure, and computing correlations between variables can show that there are many significant correlations in the data. However, it can be the case that the correlations are actually determined by the cluster structure. In this paper, we consider the problem of randomizing data so that previously discovered patterns or models are taken into account. The randomization methods can be used in iterative data mining. At each step in the data mining process, the randomization produces random samples from the set of data matrices satisfying the already discovered patterns or models. That is, given a data set and some statistics (e.g., cluster centers or co-occurrence counts) of the data, the randomization methods sample data sets having similar values of the given statistics as the original data set. We use Metropolis sampling based on local swaps to achieve this. We describe experiments on real data that demonstrate the usefulness of our approach. Our results indicate that in many cases, the results of, e.g., clustering actually imply the results of, say, frequent pattern discovery.
What is the dimension of your binary data?
Feb 04, 2019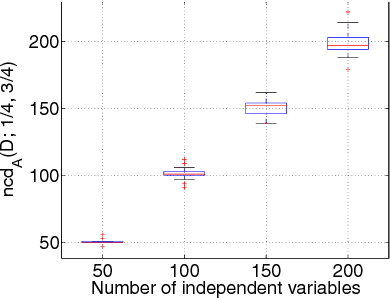
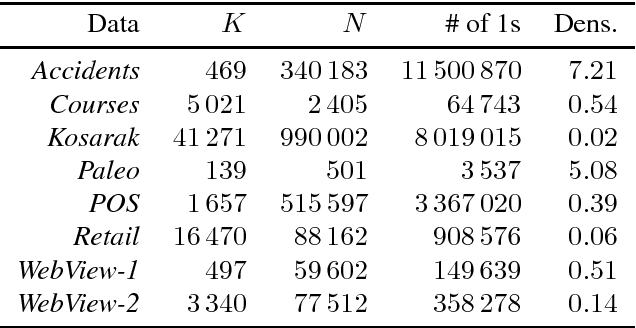
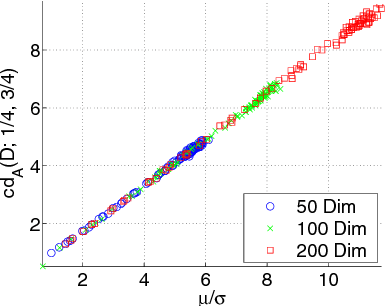
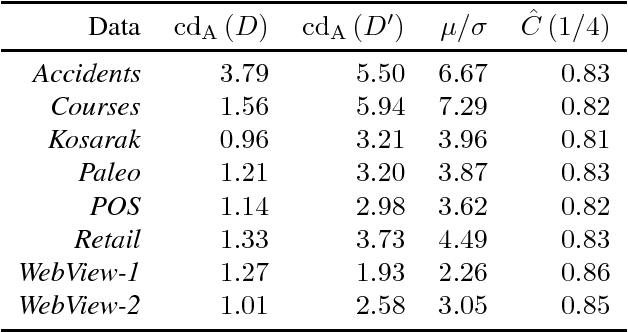
Abstract:Many 0/1 datasets have a very large number of variables; on the other hand, they are sparse and the dependency structure of the variables is simpler than the number of variables would suggest. Defining the effective dimensionality of such a dataset is a nontrivial problem. We consider the problem of defining a robust measure of dimension for 0/1 datasets, and show that the basic idea of fractal dimension can be adapted for binary data. However, as such the fractal dimension is difficult to interpret. Hence we introduce the concept of normalized fractal dimension. For a dataset $D$, its normalized fractal dimension is the number of columns in a dataset $D'$ with independent columns and having the same (unnormalized) fractal dimension as $D$. The normalized fractal dimension measures the degree of dependency structure of the data. We study the properties of the normalized fractal dimension and discuss its computation. We give empirical results on the normalized fractal dimension, comparing it against baseline measures such as PCA. We also study the relationship of the dimension of the whole dataset and the dimensions of subgroups formed by clustering. The results indicate interesting differences between and within datasets.
Probabilistic Models for Query Approximation with Large Sparse Binary Datasets
Jan 16, 2013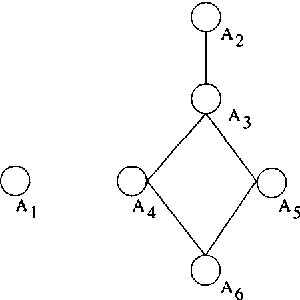
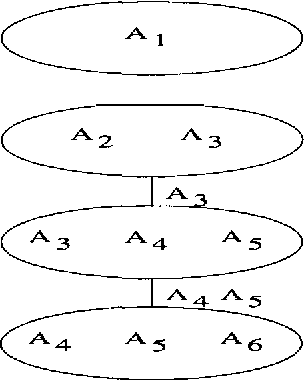
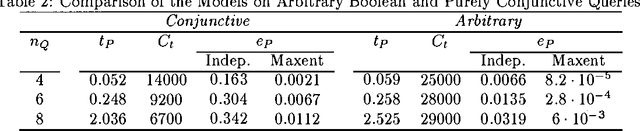
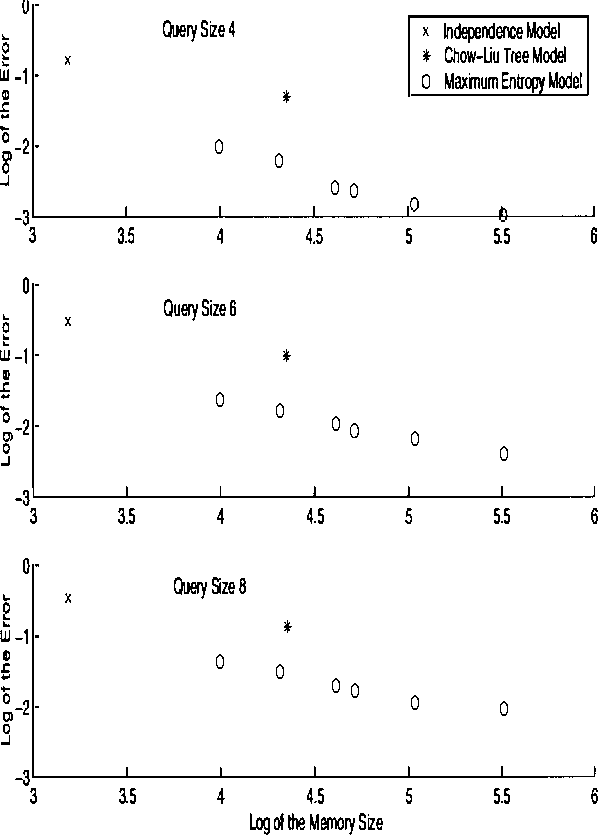
Abstract:Large sparse sets of binary transaction data with millions of records and thousands of attributes occur in various domains: customers purchasing products, users visiting web pages, and documents containing words are just three typical examples. Real-time query selectivity estimation (the problem of estimating the number of rows in the data satisfying a given predicate) is an important practical problem for such databases. We investigate the application of probabilistic models to this problem. In particular, we study a Markov random field (MRF) approach based on frequent sets and maximum entropy, and compare it to the independence model and the Chow-Liu tree model. We find that the MRF model provides substantially more accurate probability estimates than the other methods but is more expensive from a computational and memory viewpoint. To alleviate the computational requirements we show how one can apply bucket elimination and clique tree approaches to take advantage of structure in the models and in the queries. We provide experimental results on two large real-world transaction datasets.
Query Significance in Databases via Randomizations
Jun 30, 2009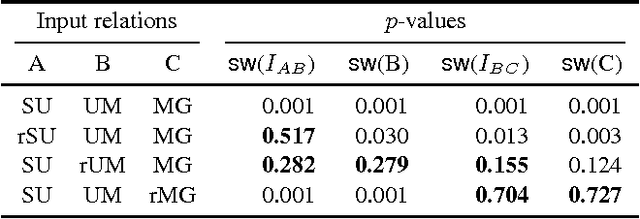
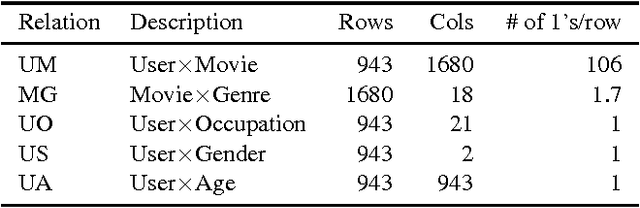
Abstract:Many sorts of structured data are commonly stored in a multi-relational format of interrelated tables. Under this relational model, exploratory data analysis can be done by using relational queries. As an example, in the Internet Movie Database (IMDb) a query can be used to check whether the average rank of action movies is higher than the average rank of drama movies. We consider the problem of assessing whether the results returned by such a query are statistically significant or just a random artifact of the structure in the data. Our approach is based on randomizing the tables occurring in the queries and repeating the original query on the randomized tables. It turns out that there is no unique way of randomizing in multi-relational data. We propose several randomization techniques, study their properties, and show how to find out which queries or hypotheses about our data result in statistically significant information. We give results on real and generated data and show how the significance of some queries vary between different randomizations.
Finding links and initiators: a graph reconstruction problem
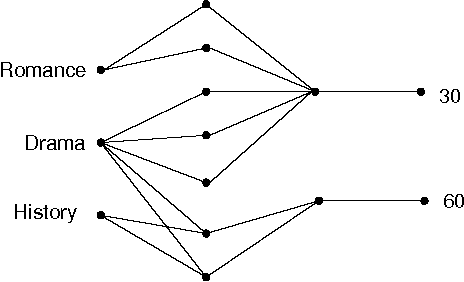
Sep 17, 2008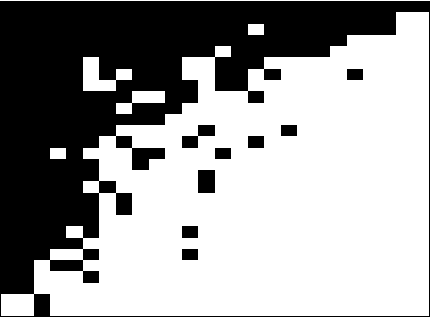

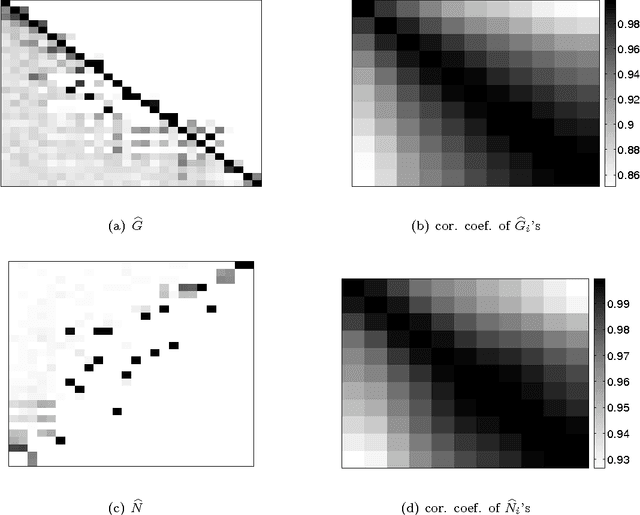
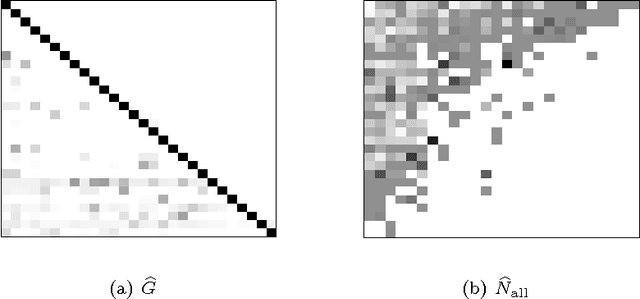
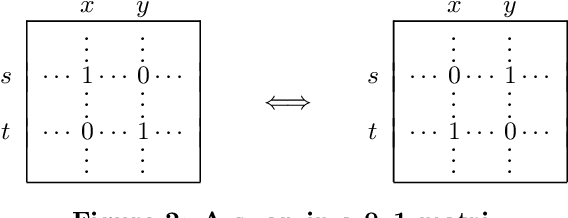
Abstract:Consider a 0-1 observation matrix M, where rows correspond to entities and columns correspond to signals; a value of 1 (or 0) in cell (i,j) of M indicates that signal j has been observed (or not observed) in entity i. Given such a matrix we study the problem of inferring the underlying directed links between entities (rows) and finding which entries in the matrix are initiators. We formally define this problem and propose an MCMC framework for estimating the links and the initiators given the matrix of observations M. We also show how this framework can be extended to incorporate a temporal aspect; instead of considering a single observation matrix M we consider a sequence of observation matrices M1,..., Mt over time. We show the connection between our problem and several problems studied in the field of social-network analysis. We apply our method to paleontological and ecological data and show that our algorithms work well in practice and give reasonable results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge