What is the dimension of your binary data?
Paper and Code
Feb 04, 2019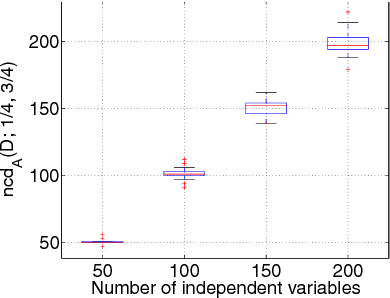
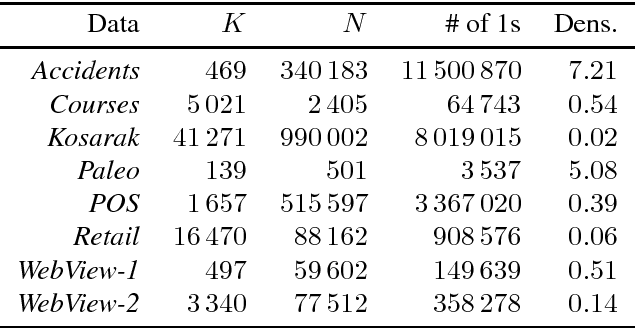
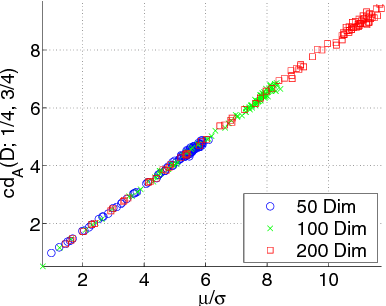
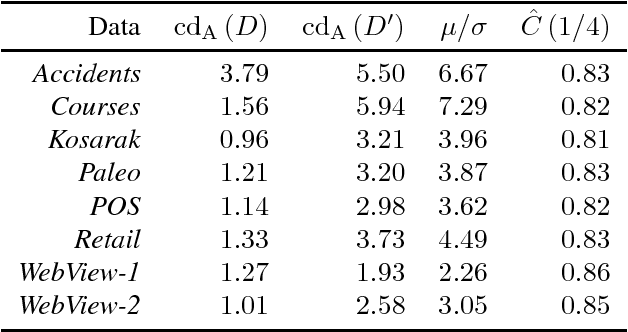
Many 0/1 datasets have a very large number of variables; on the other hand, they are sparse and the dependency structure of the variables is simpler than the number of variables would suggest. Defining the effective dimensionality of such a dataset is a nontrivial problem. We consider the problem of defining a robust measure of dimension for 0/1 datasets, and show that the basic idea of fractal dimension can be adapted for binary data. However, as such the fractal dimension is difficult to interpret. Hence we introduce the concept of normalized fractal dimension. For a dataset $D$, its normalized fractal dimension is the number of columns in a dataset $D'$ with independent columns and having the same (unnormalized) fractal dimension as $D$. The normalized fractal dimension measures the degree of dependency structure of the data. We study the properties of the normalized fractal dimension and discuss its computation. We give empirical results on the normalized fractal dimension, comparing it against baseline measures such as PCA. We also study the relationship of the dimension of the whole dataset and the dimensions of subgroups formed by clustering. The results indicate interesting differences between and within datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge