Spectral Estimation of Conditional Random Graph Models for Large-Scale Network Data

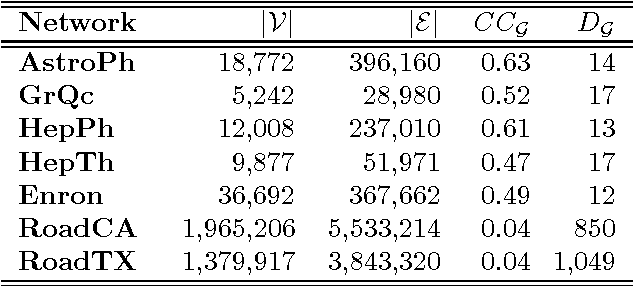
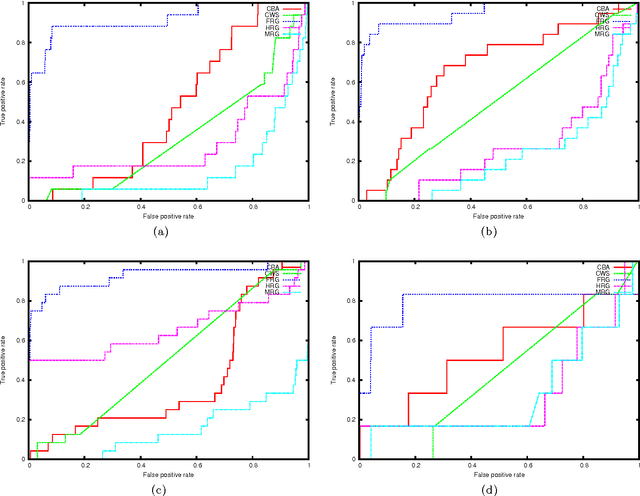
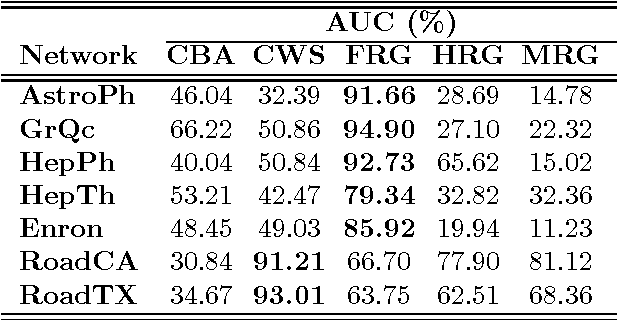
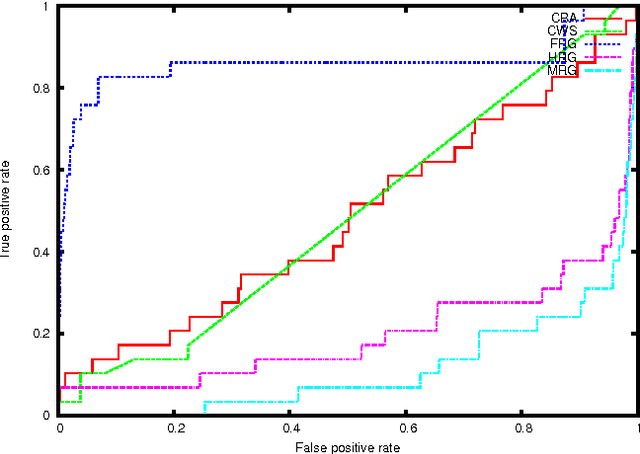
Generative models for graphs have been typically committed to strong prior assumptions concerning the form of the modeled distributions. Moreover, the vast majority of currently available models are either only suitable for characterizing some particular network properties (such as degree distribution or clustering coefficient), or they are aimed at estimating joint probability distributions, which is often intractable in large-scale networks. In this paper, we first propose a novel network statistic, based on the Laplacian spectrum of graphs, which allows to dispense with any parametric assumption concerning the modeled network properties. Second, we use the defined statistic to develop the Fiedler random graph model, switching the focus from the estimation of joint probability distributions to a more tractable conditional estimation setting. After analyzing the dependence structure characterizing Fiedler random graphs, we evaluate them experimentally in edge prediction over several real-world networks, showing that they allow to reach a much higher prediction accuracy than various alternative statistical models.

Query Significance in Databases via Randomizations

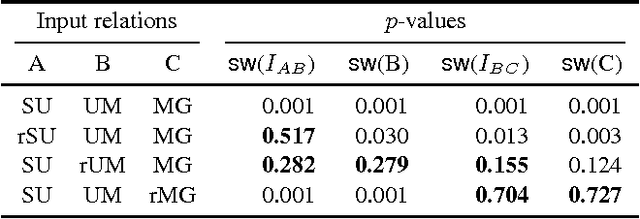
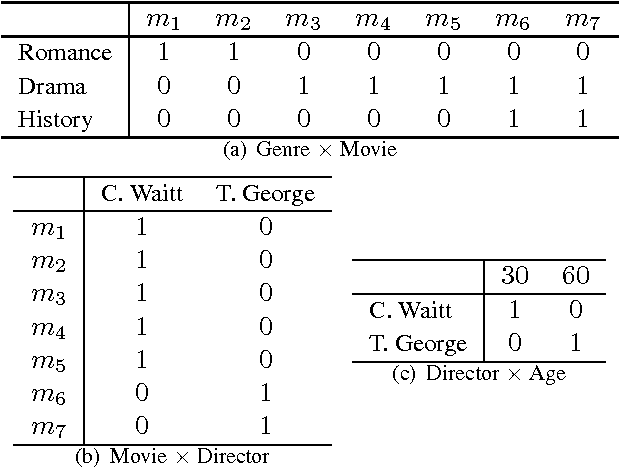
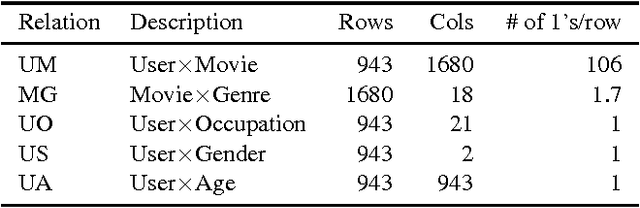
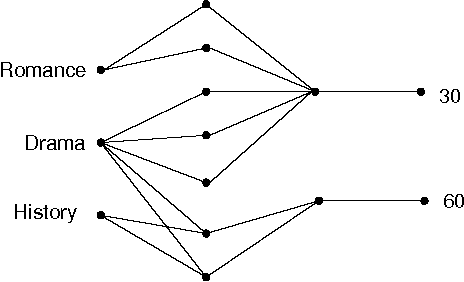
Many sorts of structured data are commonly stored in a multi-relational format of interrelated tables. Under this relational model, exploratory data analysis can be done by using relational queries. As an example, in the Internet Movie Database (IMDb) a query can be used to check whether the average rank of action movies is higher than the average rank of drama movies. We consider the problem of assessing whether the results returned by such a query are statistically significant or just a random artifact of the structure in the data. Our approach is based on randomizing the tables occurring in the queries and repeating the original query on the randomized tables. It turns out that there is no unique way of randomizing in multi-relational data. We propose several randomization techniques, study their properties, and show how to find out which queries or hypotheses about our data result in statistically significant information. We give results on real and generated data and show how the significance of some queries vary between different randomizations.

Multiple Hypothesis Testing in Pattern Discovery

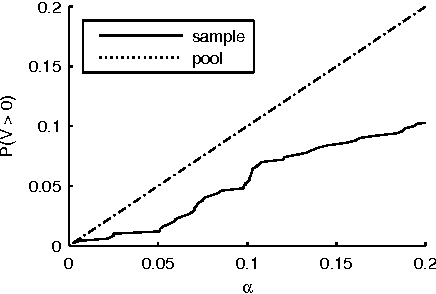
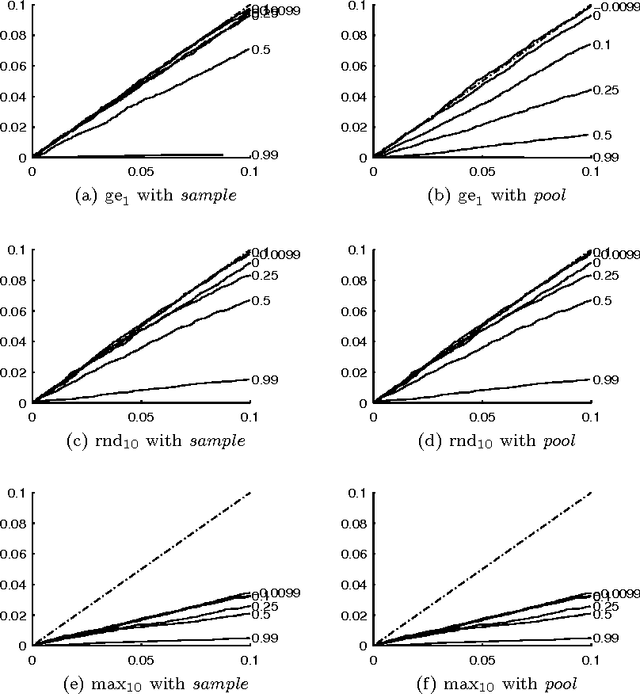
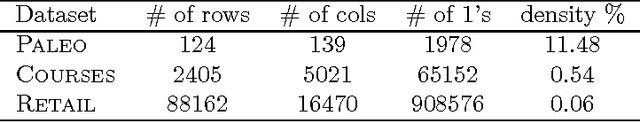
The problem of multiple hypothesis testing arises when there are more than one hypothesis to be tested simultaneously for statistical significance. This is a very common situation in many data mining applications. For instance, assessing simultaneously the significance of all frequent itemsets of a single dataset entails a host of hypothesis, one for each itemset. A multiple hypothesis testing method is needed to control the number of false positives (Type I error). Our contribution in this paper is to extend the multiple hypothesis framework to be used with a generic data mining algorithm. We provide a method that provably controls the family-wise error rate (FWER, the probability of at least one false positive) in the strong sense. We evaluate the performance of our solution on both real and generated data. The results show that our method controls the FWER while maintaining the power of the test.

An Approximation Ratio for Biclustering

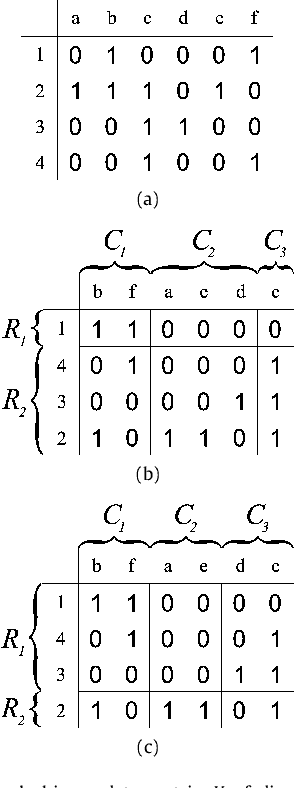
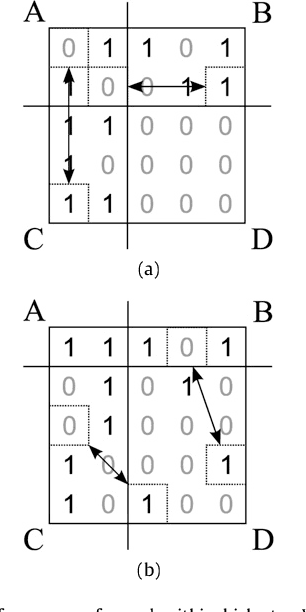
The problem of biclustering consists of the simultaneous clustering of rows and columns of a matrix such that each of the submatrices induced by a pair of row and column clusters is as uniform as possible. In this paper we approximate the optimal biclustering by applying one-way clustering algorithms independently on the rows and on the columns of the input matrix. We show that such a solution yields a worst-case approximation ratio of 1+sqrt(2) under L1-norm for 0-1 valued matrices, and of 2 under L2-norm for real valued matrices.