Multiple Hypothesis Testing in Pattern Discovery
Paper and Code
Jun 29, 2009
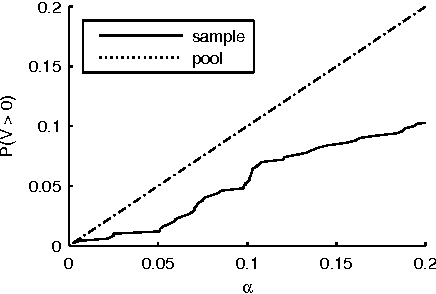
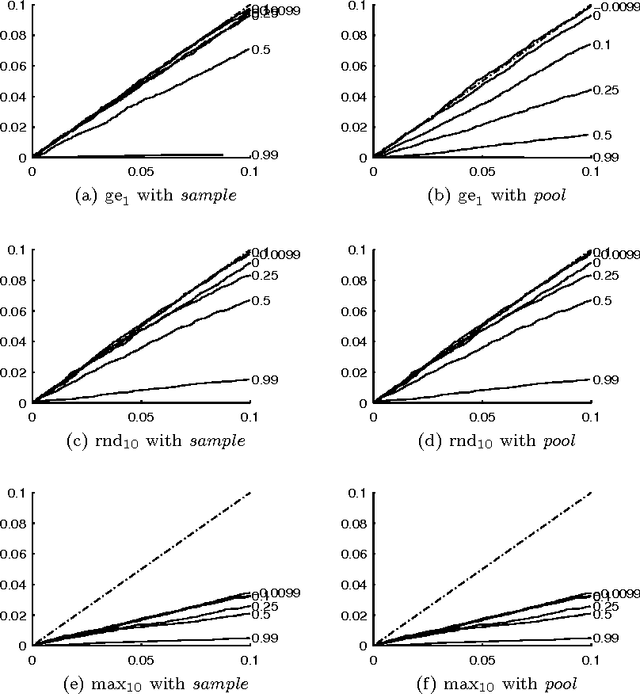
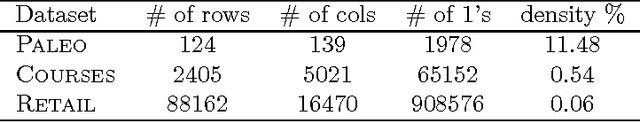
The problem of multiple hypothesis testing arises when there are more than one hypothesis to be tested simultaneously for statistical significance. This is a very common situation in many data mining applications. For instance, assessing simultaneously the significance of all frequent itemsets of a single dataset entails a host of hypothesis, one for each itemset. A multiple hypothesis testing method is needed to control the number of false positives (Type I error). Our contribution in this paper is to extend the multiple hypothesis framework to be used with a generic data mining algorithm. We provide a method that provably controls the family-wise error rate (FWER, the probability of at least one false positive) in the strong sense. We evaluate the performance of our solution on both real and generated data. The results show that our method controls the FWER while maintaining the power of the test.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge