Consistent Multigroup Low-Rank Approximation

We consider the problem of consistent low-rank approximation for multigroup data: we ask for a sequence of $k$ basis vectors such that projecting the data onto their spanned subspace treats all groups as equally as possible, by minimizing the maximum error among the groups. Additionally, we require that the sequence of basis vectors satisfies the natural consistency property: when looking for the best $k$ vectors, the first $d<k$ vectors are the best possible solution to the problem of finding $d$ basis vectors. Thus, this multigroup low-rank approximation method naturally generalizes \svd and reduces to \svd for data with a single group. We give an iterative algorithm for this task that sequentially adds to the basis the vector that gives the best rank$-1$ projection according to the min-max criterion, and then projects the data onto the orthogonal complement of that vector. For finding the best rank$-1$ projection, we use primal-dual approaches or semidefinite programming. We analyze the theoretical properties of the algorithms and demonstrate empirically that the proposed methods compare favorably to existing methods for multigroup (or fair) PCA.

Efficient Exploration of the Rashomon Set of Rule Set Models

Today, as increasingly complex predictive models are developed, simple rule sets remain a crucial tool to obtain interpretable predictions and drive high-stakes decision making. However, a single rule set provides a partial representation of a learning task. An emerging paradigm in interpretable machine learning aims at exploring the Rashomon set of all models exhibiting near-optimal performance. Existing work on Rashomon-set exploration focuses on exhaustive search of the Rashomon set for particular classes of models, which can be a computationally challenging task. On the other hand, exhaustive enumeration leads to redundancy that often is not necessary, and a representative sample or an estimate of the size of the Rashomon set is sufficient for many applications. In this work, we propose, for the first time, efficient methods to explore the Rashomon set of rule set models with or without exhaustive search. Extensive experiments demonstrate the effectiveness of the proposed methods in a variety of scenarios.

Concise and interpretable multi-label rule sets

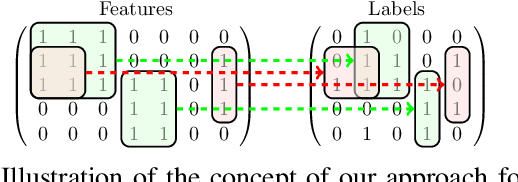
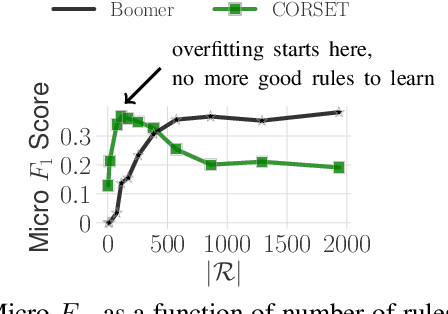
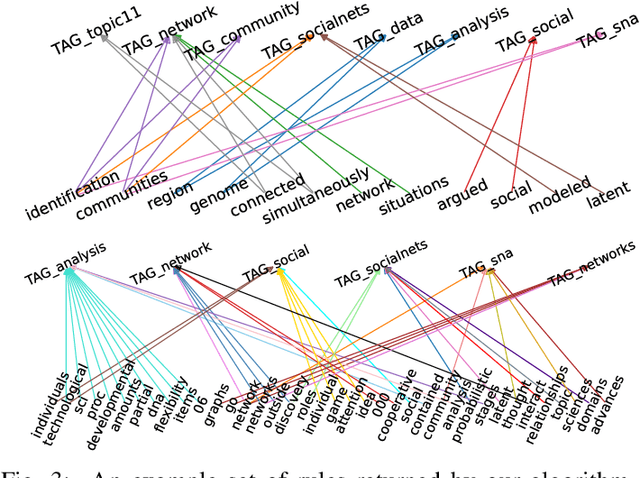
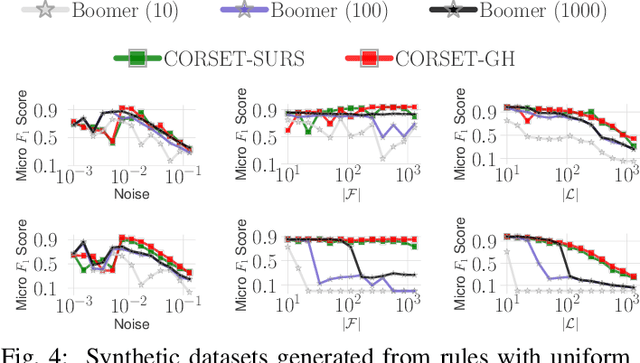
Multi-label classification is becoming increasingly ubiquitous, but not much attention has been paid to interpretability. In this paper, we develop a multi-label classifier that can be represented as a concise set of simple "if-then" rules, and thus, it offers better interpretability compared to black-box models. Notably, our method is able to find a small set of relevant patterns that lead to accurate multi-label classification, while existing rule-based classifiers are myopic and wasteful in searching rules,requiring a large number of rules to achieve high accuracy. In particular, we formulate the problem of choosing multi-label rules to maximize a target function, which considers not only discrimination ability with respect to labels, but also diversity. Accounting for diversity helps to avoid redundancy, and thus, to control the number of rules in the solution set. To tackle the said maximization problem we propose a 2-approximation algorithm, which relies on a novel technique to sample high-quality rules. In addition to our theoretical analysis, we provide a thorough experimental evaluation, which indicates that our approach offers a trade-off between predictive performance and interpretability that is unmatched in previous work.