Consistent Multigroup Low-Rank Approximation

We consider the problem of consistent low-rank approximation for multigroup data: we ask for a sequence of $k$ basis vectors such that projecting the data onto their spanned subspace treats all groups as equally as possible, by minimizing the maximum error among the groups. Additionally, we require that the sequence of basis vectors satisfies the natural consistency property: when looking for the best $k$ vectors, the first $d<k$ vectors are the best possible solution to the problem of finding $d$ basis vectors. Thus, this multigroup low-rank approximation method naturally generalizes \svd and reduces to \svd for data with a single group. We give an iterative algorithm for this task that sequentially adds to the basis the vector that gives the best rank$-1$ projection according to the min-max criterion, and then projects the data onto the orthogonal complement of that vector. For finding the best rank$-1$ projection, we use primal-dual approaches or semidefinite programming. We analyze the theoretical properties of the algorithms and demonstrate empirically that the proposed methods compare favorably to existing methods for multigroup (or fair) PCA.

Fair Column Subset Selection

We consider the problem of fair column subset selection. In particular, we assume that two groups are present in the data, and the chosen column subset must provide a good approximation for both, relative to their respective best rank-k approximations. We show that this fair setting introduces significant challenges: in order to extend known results, one cannot do better than the trivial solution of simply picking twice as many columns as the original methods. We adopt a known approach based on deterministic leverage-score sampling, and show that merely sampling a subset of appropriate size becomes NP-hard in the presence of two groups. Whereas finding a subset of two times the desired size is trivial, we provide an efficient algorithm that achieves the same guarantees with essentially 1.5 times that size. We validate our methods through an extensive set of experiments on real-world data.

Generalized Leverage Scores: Geometric Interpretation and Applications

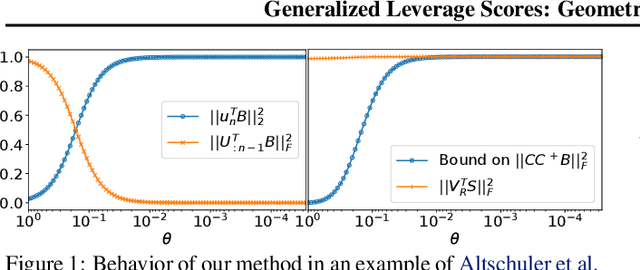
In problems involving matrix computations, the concept of leverage has found a large number of applications. In particular, leverage scores, which relate the columns of a matrix to the subspaces spanned by its leading singular vectors, are helpful in revealing column subsets to approximately factorize a matrix with quality guarantees. As such, they provide a solid foundation for a variety of machine-learning methods. In this paper we extend the definition of leverage scores to relate the columns of a matrix to arbitrary subsets of singular vectors. We establish a precise connection between column and singular-vector subsets, by relating the concepts of leverage scores and principal angles between subspaces. We employ this result to design approximation algorithms with provable guarantees for two well-known problems: generalized column subset selection and sparse canonical correlation analysis. We run numerical experiments to provide further insight on the proposed methods. The novel bounds we derive improve our understanding of fundamental concepts in matrix approximations. In addition, our insights may serve as building blocks for further contributions.