Diversity-aware clustering: Computational Complexity and Approximation Algorithms

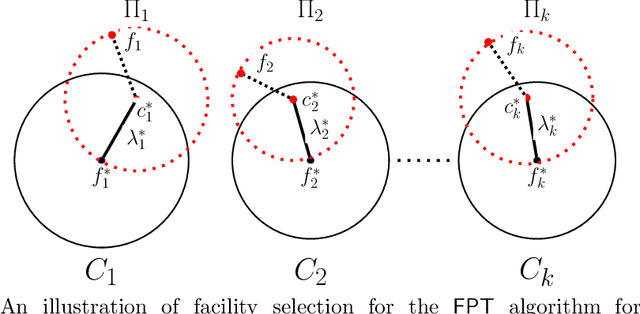
In this work, we study diversity-aware clustering problems where the data points are associated with multiple attributes resulting in intersecting groups. A clustering solution need to ensure that a minimum number of cluster centers are chosen from each group while simultaneously minimizing the clustering objective, which can be either $k$-median, $k$-means or $k$-supplier. We present parameterized approximation algorithms with approximation ratios $1+ \frac{2}{e}$, $1+\frac{8}{e}$ and $3$ for diversity-aware $k$-median, diversity-aware $k$-means and diversity-aware $k$-supplier, respectively. The approximation ratios are tight assuming Gap-ETH and FPT $\neq$ W[2]. For fair $k$-median and fair $k$-means with disjoint faicility groups, we present parameterized approximation algorithm with approximation ratios $1+\frac{2}{e}$ and $1+\frac{8}{e}$, respectively. For fair $k$-supplier with disjoint facility groups, we present a polynomial-time approximation algorithm with factor $3$, improving the previous best known approximation ratio of factor $5$.

Fair Column Subset Selection

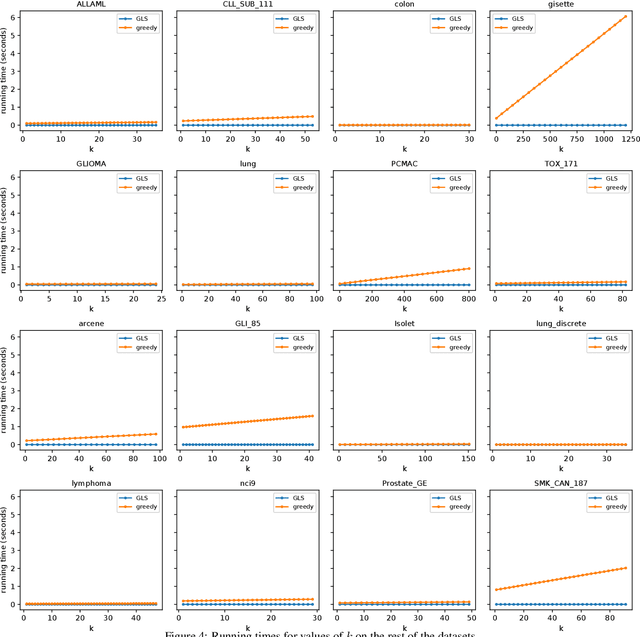
We consider the problem of fair column subset selection. In particular, we assume that two groups are present in the data, and the chosen column subset must provide a good approximation for both, relative to their respective best rank-k approximations. We show that this fair setting introduces significant challenges: in order to extend known results, one cannot do better than the trivial solution of simply picking twice as many columns as the original methods. We adopt a known approach based on deterministic leverage-score sampling, and show that merely sampling a subset of appropriate size becomes NP-hard in the presence of two groups. Whereas finding a subset of two times the desired size is trivial, we provide an efficient algorithm that achieves the same guarantees with essentially 1.5 times that size. We validate our methods through an extensive set of experiments on real-world data.

Generalized Leverage Scores: Geometric Interpretation and Applications

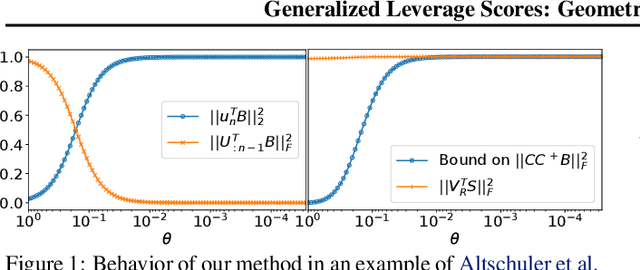
In problems involving matrix computations, the concept of leverage has found a large number of applications. In particular, leverage scores, which relate the columns of a matrix to the subspaces spanned by its leading singular vectors, are helpful in revealing column subsets to approximately factorize a matrix with quality guarantees. As such, they provide a solid foundation for a variety of machine-learning methods. In this paper we extend the definition of leverage scores to relate the columns of a matrix to arbitrary subsets of singular vectors. We establish a precise connection between column and singular-vector subsets, by relating the concepts of leverage scores and principal angles between subspaces. We employ this result to design approximation algorithms with provable guarantees for two well-known problems: generalized column subset selection and sparse canonical correlation analysis. We run numerical experiments to provide further insight on the proposed methods. The novel bounds we derive improve our understanding of fundamental concepts in matrix approximations. In addition, our insights may serve as building blocks for further contributions.

Off-the-grid: Fast and Effective Hyperparameter Search for Kernel Clustering

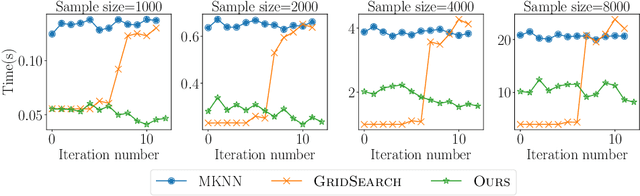
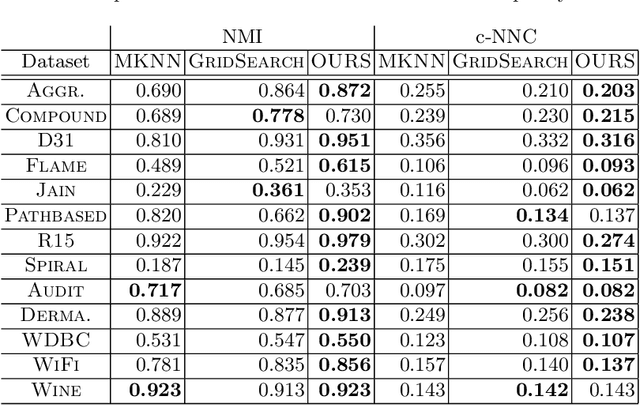
Kernel functions are a powerful tool to enhance the $k$-means clustering algorithm via the kernel trick. It is known that the parameters of the chosen kernel function can have a dramatic impact on the result. In supervised settings, these can be tuned via cross-validation, but for clustering this is not straightforward and heuristics are usually employed. In this paper we study the impact of kernel parameters on kernel $k$-means. In particular, we derive a lower bound, tight up to constant factors, below which the parameter of the RBF kernel will render kernel $k$-means meaningless. We argue that grid search can be ineffective for hyperparameter search in this context and propose an alternative algorithm for this purpose. In addition, we offer an efficient implementation based on fast approximate exponentiation with provable quality guarantees. Our experimental results demonstrate the ability of our method to efficiently reveal a rich and useful set of hyperparameter values.

Regularized Greedy Column Subset Selection

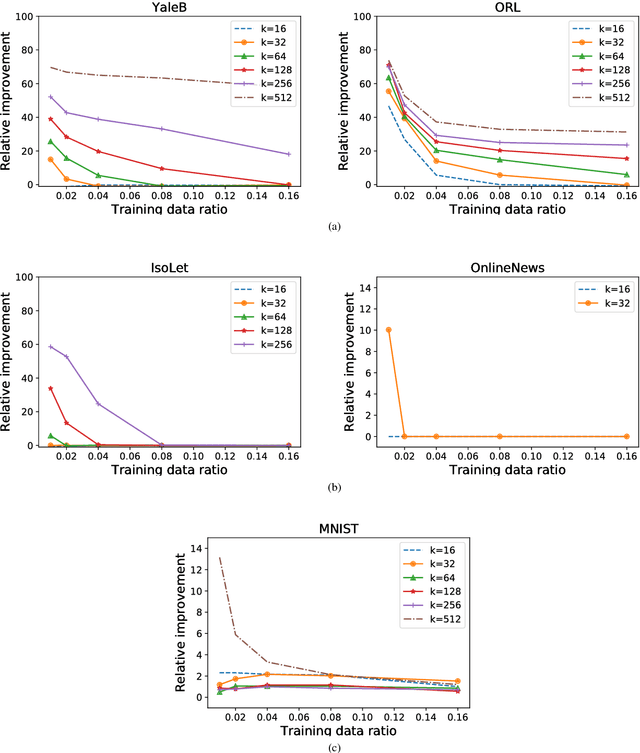
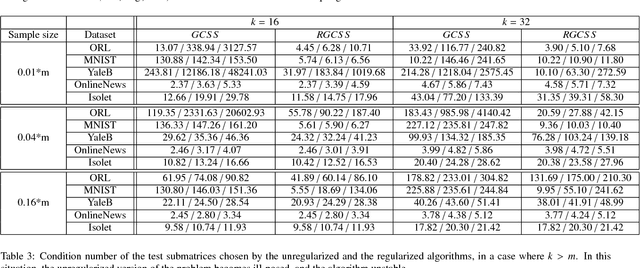
The Column Subset Selection Problem provides a natural framework for unsupervised feature selection. Despite being a hard combinatorial optimization problem, there exist efficient algorithms that provide good approximations. The drawback of the problem formulation is that it incorporates no form of regularization, and is therefore very sensitive to noise when presented with scarce data. In this paper we propose a regularized formulation of this problem, and derive a correct greedy algorithm that is similar in efficiency to existing greedy methods for the unregularized problem. We study its adequacy for feature selection and propose suitable formulations. Additionally, we derive a lower bound for the error of the proposed problems. Through various numerical experiments on real and synthetic data, we demonstrate the significantly increased robustness and stability of our method, as well as the improved conditioning of its output, all while remaining efficient for practical use.

Using Machine Learning to Detect Noisy Neighbors in 5G Networks

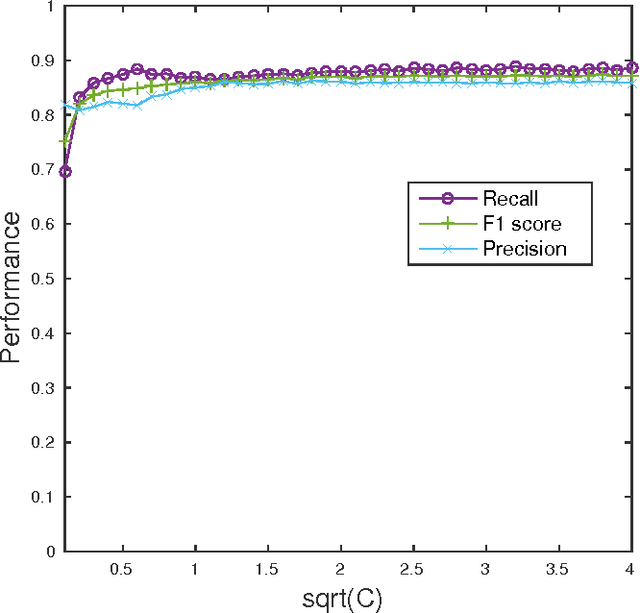
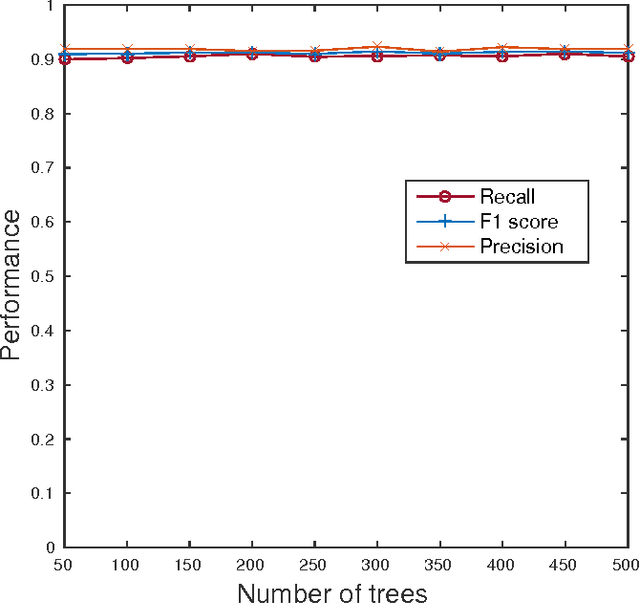
5G networks are expected to be more dynamic and chaotic in their structure than current networks. With the advent of Network Function Virtualization (NFV), Network Functions (NF) will no longer be tightly coupled with the hardware they are running on, which poses new challenges in network management. Noisy neighbor is a term commonly used to describe situations in NFV infrastructure where an application experiences degradation in performance due to the fact that some of the resources it needs are occupied by other applications in the same cloud node. These situations cannot be easily identified using straightforward approaches, which calls for the use of sophisticated methods for NFV infrastructure management. In this paper we demonstrate how Machine Learning (ML) techniques can be used to identify such events. Through experiments using data collected at real NFV infrastructure, we show that standard models for automated classification can detect the noisy neighbor phenomenon with an accuracy of more than 90% in a simple scenario.