Off-the-grid: Fast and Effective Hyperparameter Search for Kernel Clustering

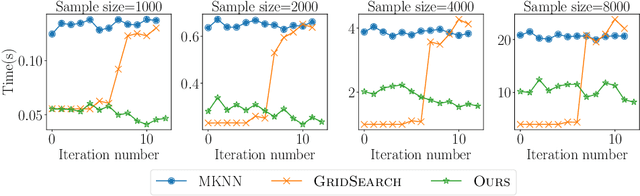
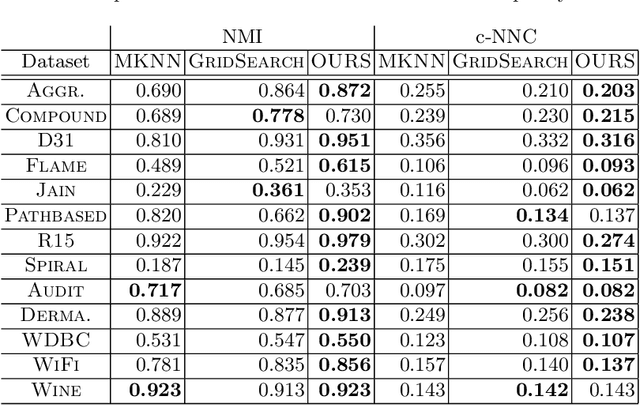
Kernel functions are a powerful tool to enhance the $k$-means clustering algorithm via the kernel trick. It is known that the parameters of the chosen kernel function can have a dramatic impact on the result. In supervised settings, these can be tuned via cross-validation, but for clustering this is not straightforward and heuristics are usually employed. In this paper we study the impact of kernel parameters on kernel $k$-means. In particular, we derive a lower bound, tight up to constant factors, below which the parameter of the RBF kernel will render kernel $k$-means meaningless. We argue that grid search can be ineffective for hyperparameter search in this context and propose an alternative algorithm for this purpose. In addition, we offer an efficient implementation based on fast approximate exponentiation with provable quality guarantees. Our experimental results demonstrate the ability of our method to efficiently reveal a rich and useful set of hyperparameter values.

Double Relief with progressive weighting function

Feature weighting algorithms try to solve a problem of great importance nowadays in machine learning: The search of a relevance measure for the features of a given domain. This relevance is primarily used for feature selection as feature weighting can be seen as a generalization of it, but it is also useful to better understand a problem's domain or to guide an inductor in its learning process. Relief family of algorithms are proven to be very effective in this task. On previous work, a new extension was proposed that aimed for improving the algorithm's performance and it was shown that in certain cases it improved the weights' estimation accuracy. However, it also seemed to be sensible to some characteristics of the data. An improvement of that previously presented extension is presented in this work that aims to make it more robust to problem specific characteristics. An experimental design is proposed to test its performance. Results of the tests prove that it indeed increase the robustness of the previously proposed extension.

Toward better feature weighting algorithms: a focus on Relief

Feature weighting algorithms try to solve a problem of great importance nowadays in machine learning: The search of a relevance measure for the features of a given domain. This relevance is primarily used for feature selection as feature weighting can be seen as a generalization of it, but it is also useful to better understand a problem's domain or to guide an inductor in its learning process. Relief family of algorithms are proven to be very effective in this task. Some other feature weighting methods are reviewed in order to give some context and then the different existing extensions to the original algorithm are explained. One of Relief's known issues is the performance degradation of its estimates when redundant features are present. A novel theoretical definition of redundancy level is given in order to guide the work towards an extension of the algorithm that is more robust against redundancy. A new extension is presented that aims for improving the algorithms performance. Some experiments were driven to test this new extension against the existing ones with a set of artificial and real datasets and denoted that in certain cases it improves the weight's estimation accuracy.