Evaluation of Large Language Models via Coupled Token Generation

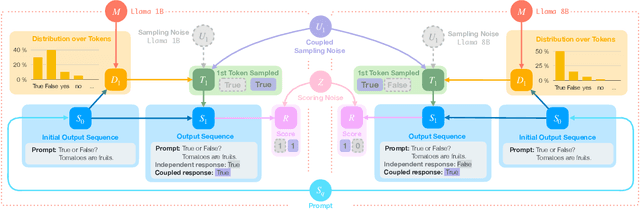
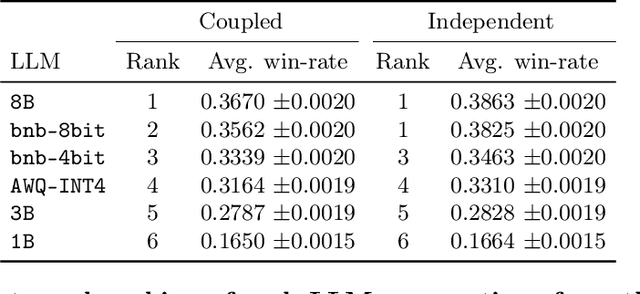
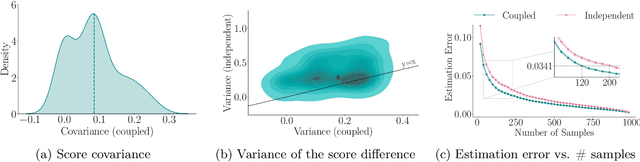
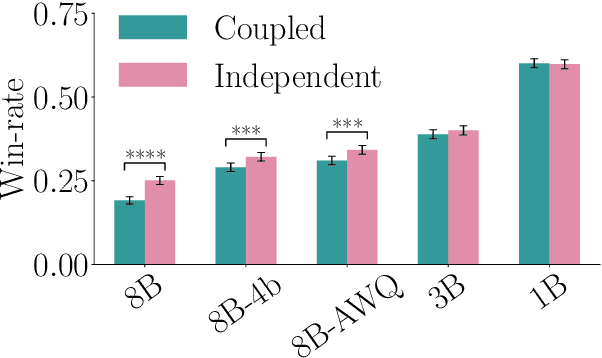
State of the art large language models rely on randomization to respond to a prompt. As an immediate consequence, a model may respond differently to the same prompt if asked multiple times. In this work, we argue that the evaluation and ranking of large language models should control for the randomization underpinning their functioning. Our starting point is the development of a causal model for coupled autoregressive generation, which allows different large language models to sample responses with the same source of randomness. Building upon our causal model, we first show that, on evaluations based on benchmark datasets, coupled autoregressive generation leads to the same conclusions as vanilla autoregressive generation but using provably fewer samples. However, we further show that, on evaluations based on (human) pairwise comparisons, coupled and vanilla autoregressive generation can surprisingly lead to different rankings when comparing more than two models, even with an infinite amount of samples. This suggests that the apparent advantage of a model over others in existing evaluation protocols may not be genuine but rather confounded by the randomness inherent to the generation process. To illustrate and complement our theoretical results, we conduct experiments with several large language models from the Llama family. We find that, across multiple knowledge areas from the popular MMLU benchmark dataset, coupled autoregressive generation requires up to 40% fewer samples to reach the same conclusions as vanilla autoregressive generation. Further, using data from the LMSYS Chatbot Arena platform, we find that the win-rates derived from pairwise comparisons by a strong large language model to prompts differ under coupled and vanilla autoregressive generation.

Fair Clustering for Data Summarization: Improved Approximation Algorithms and Complexity Insights

Data summarization tasks are often modeled as $k$-clustering problems, where the goal is to choose $k$ data points, called cluster centers, that best represent the dataset by minimizing a clustering objective. A popular objective is to minimize the maximum distance between any data point and its nearest center, which is formalized as the $k$-center problem. While in some applications all data points can be chosen as centers, in the general setting, centers must be chosen from a predefined subset of points, referred as facilities or suppliers; this is known as the $k$-supplier problem. In this work, we focus on fair data summarization modeled as the fair $k$-supplier problem, where data consists of several groups, and a minimum number of centers must be selected from each group while minimizing the $k$-supplier objective. The groups can be disjoint or overlapping, leading to two distinct problem variants each with different computational complexity. We present $3$-approximation algorithms for both variants, improving the previously known factor of $5$. For disjoint groups, our algorithm runs in polynomial time, while for overlapping groups, we present a fixed-parameter tractable algorithm, where the exponential runtime depends only on the number of groups and centers. We show that these approximation factors match the theoretical lower bounds, assuming standard complexity theory conjectures. Finally, using an open-source implementation, we demonstrate the scalability of our algorithms on large synthetic datasets and assess the price of fairness on real-world data, comparing solution quality with and without fairness constraints.

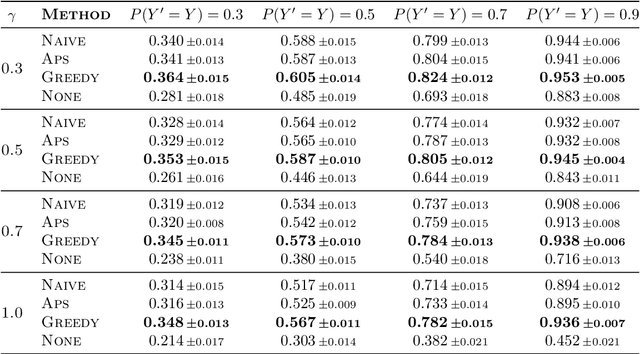
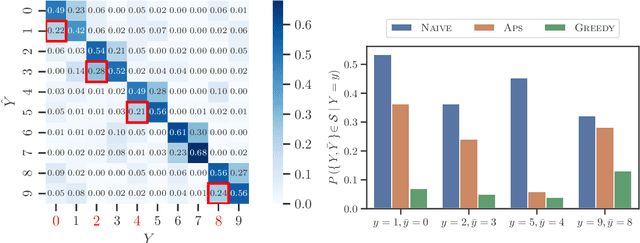
Controlling Counterfactual Harm in Decision Support Systems Based on Prediction Sets

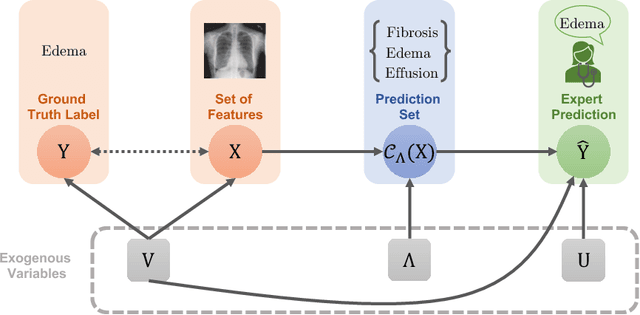
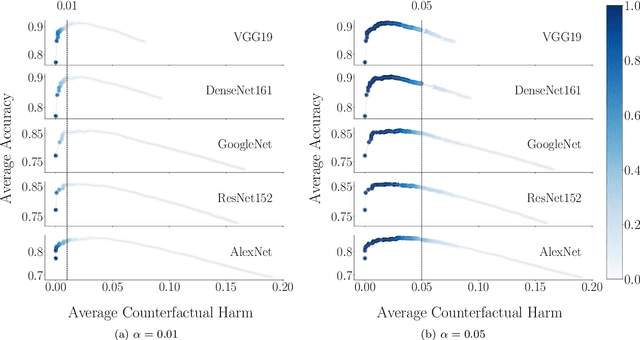
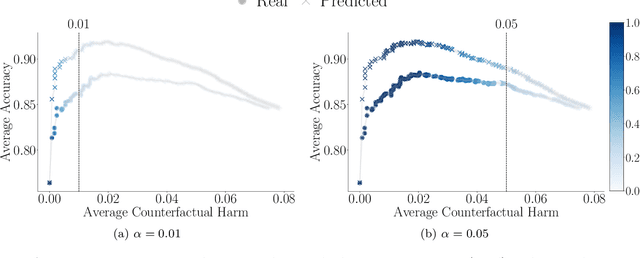
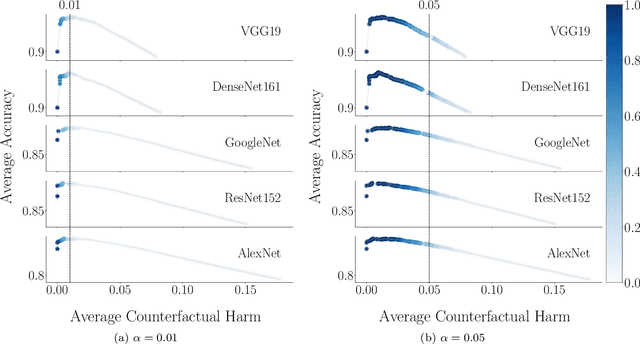
Decision support systems based on prediction sets help humans solve multiclass classification tasks by narrowing down the set of potential label values to a subset of them, namely a prediction set, and asking them to always predict label values from the prediction sets. While this type of systems have been proven to be effective at improving the average accuracy of the predictions made by humans, by restricting human agency, they may cause harm$\unicode{x2014}$a human who has succeeded at predicting the ground-truth label of an instance on their own may have failed had they used these systems. In this paper, our goal is to control how frequently a decision support system based on prediction sets may cause harm, by design. To this end, we start by characterizing the above notion of harm using the theoretical framework of structural causal models. Then, we show that, under a natural, albeit unverifiable, monotonicity assumption, we can estimate how frequently a system may cause harm using only predictions made by humans on their own. Further, we also show that, under a weaker monotonicity assumption, which can be verified experimentally, we can bound how frequently a system may cause harm again using only predictions made by humans on their own. Building upon these assumptions, we introduce a computational framework to design decision support systems based on prediction sets that are guaranteed to cause harm less frequently than a user-specified value using conformal risk control. We validate our framework using real human predictions from two different human subject studies and show that, in decision support systems based on prediction sets, there is a trade-off between accuracy and counterfactual harm.

Towards Human-AI Complementarity with Predictions Sets

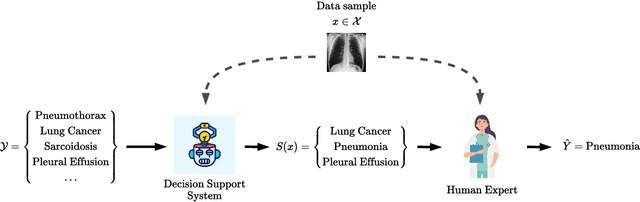
Decision support systems based on prediction sets have proven to be effective at helping human experts solve classification tasks. Rather than providing single-label predictions, these systems provide sets of label predictions constructed using conformal prediction, namely prediction sets, and ask human experts to predict label values from these sets. In this paper, we first show that the prediction sets constructed using conformal prediction are, in general, suboptimal in terms of average accuracy. Then, we show that the problem of finding the optimal prediction sets under which the human experts achieve the highest average accuracy is NP-hard. More strongly, unless P = NP, we show that the problem is hard to approximate to any factor less than the size of the label set. However, we introduce a simple and efficient greedy algorithm that, for a large class of expert models and non-conformity scores, is guaranteed to find prediction sets that provably offer equal or greater performance than those constructed using conformal prediction. Further, using a simulation study with both synthetic and real expert predictions, we demonstrate that, in practice, our greedy algorithm finds near-optimal prediction sets offering greater performance than conformal prediction.

Prediction-Powered Ranking of Large Language Models

Large language models are often ranked according to their level of alignment with human preferences -- a model is better than other models if its outputs are more frequently preferred by humans. One of the most popular ways to elicit human preferences utilizes pairwise comparisons between the outputs provided by different models to the same inputs. However, since gathering pairwise comparisons by humans is costly and time-consuming, it has become a very common practice to gather pairwise comparisons by a strong large language model -- a model strongly aligned with human preferences. Surprisingly, practitioners cannot currently measure the uncertainty that any mismatch between human and model preferences may introduce in the constructed rankings. In this work, we develop a statistical framework to bridge this gap. Given a small set of pairwise comparisons by humans and a large set of pairwise comparisons by a model, our framework provides a rank-set -- a set of possible ranking positions -- for each of the models under comparison. Moreover, it guarantees that, with a probability greater than or equal to a user-specified value, the rank-sets cover the true ranking consistent with (the distribution of) human pairwise preferences. Our framework is computationally efficient, easy to use, and does not make any assumption about the distribution of human preferences nor about the degree of alignment between the pairwise comparisons by the humans and the strong large language model.

Diversity-aware clustering: Computational Complexity and Approximation Algorithms

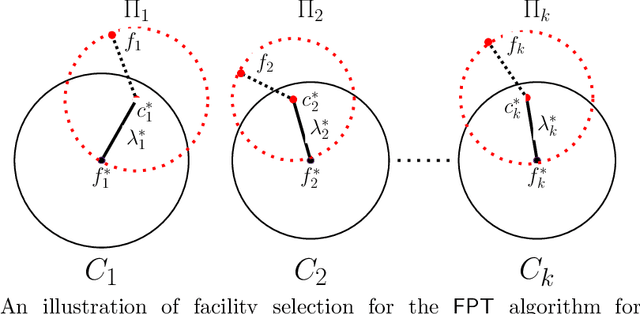
In this work, we study diversity-aware clustering problems where the data points are associated with multiple attributes resulting in intersecting groups. A clustering solution need to ensure that a minimum number of cluster centers are chosen from each group while simultaneously minimizing the clustering objective, which can be either $k$-median, $k$-means or $k$-supplier. We present parameterized approximation algorithms with approximation ratios $1+ \frac{2}{e}$, $1+\frac{8}{e}$ and $3$ for diversity-aware $k$-median, diversity-aware $k$-means and diversity-aware $k$-supplier, respectively. The approximation ratios are tight assuming Gap-ETH and FPT $\neq$ W[2]. For fair $k$-median and fair $k$-means with disjoint faicility groups, we present parameterized approximation algorithm with approximation ratios $1+\frac{2}{e}$ and $1+\frac{8}{e}$, respectively. For fair $k$-supplier with disjoint facility groups, we present a polynomial-time approximation algorithm with factor $3$, improving the previous best known approximation ratio of factor $5$.

Fair Column Subset Selection

We consider the problem of fair column subset selection. In particular, we assume that two groups are present in the data, and the chosen column subset must provide a good approximation for both, relative to their respective best rank-k approximations. We show that this fair setting introduces significant challenges: in order to extend known results, one cannot do better than the trivial solution of simply picking twice as many columns as the original methods. We adopt a known approach based on deterministic leverage-score sampling, and show that merely sampling a subset of appropriate size becomes NP-hard in the presence of two groups. Whereas finding a subset of two times the desired size is trivial, we provide an efficient algorithm that achieves the same guarantees with essentially 1.5 times that size. We validate our methods through an extensive set of experiments on real-world data.