Ranking with submodular functions on a budget
Paper and Code
Apr 08, 2022
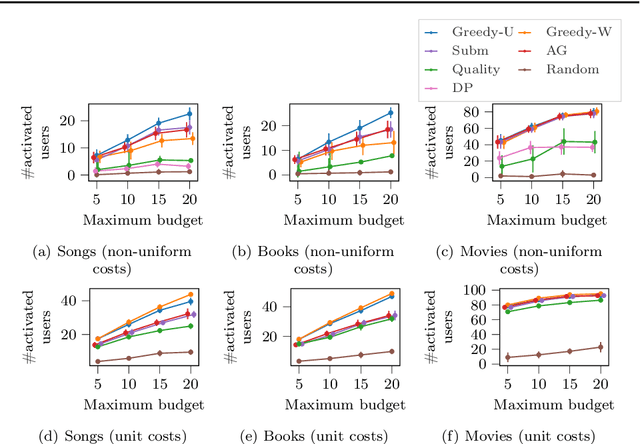


Submodular maximization has been the backbone of many important machine-learning problems, and has applications to viral marketing, diversification, sensor placement, and more. However, the study of maximizing submodular functions has mainly been restricted in the context of selecting a set of items. On the other hand, many real-world applications require a solution that is a ranking over a set of items. The problem of ranking in the context of submodular function maximization has been considered before, but to a much lesser extent than item-selection formulations. In this paper, we explore a novel formulation for ranking items with submodular valuations and budget constraints. We refer to this problem as max-submodular ranking (MSR). In more detail, given a set of items and a set of non-decreasing submodular functions, where each function is associated with a budget, we aim to find a ranking of the set of items that maximizes the sum of values achieved by all functions under the budget constraints. For the MSR problem with cardinality- and knapsack-type budget constraints we propose practical algorithms with approximation guarantees. In addition, we perform an empirical evaluation, which demonstrates the superior performance of the proposed algorithms against strong baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge