Scalable Dyadic Independence Models with Local and Global Constraints

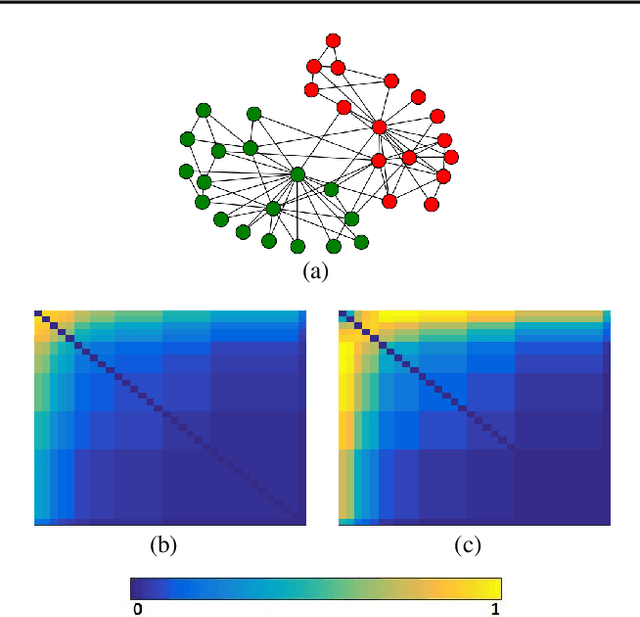
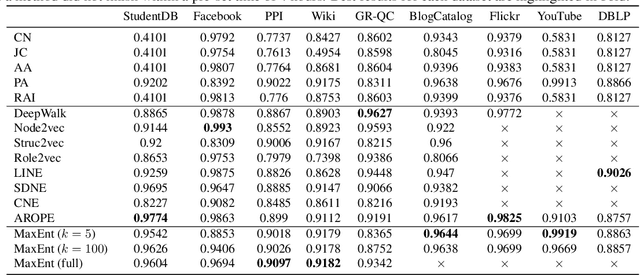
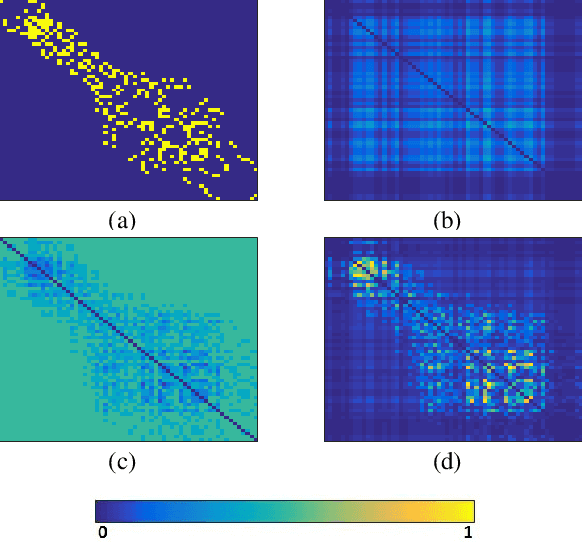
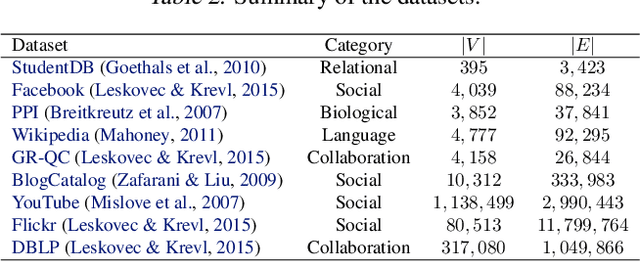
An important challenge in the field of exponential random graphs (ERGs) is the fitting of non-trivial ERGs on large networks. By utilizing matrix block-approximation techniques, we propose an approximative framework to such non-trivial ERGs that result in dyadic independence (i.e., edge independent) models, while being able to meaningfully model local information (degrees) as well as global information (clustering coefficient, assortativity, etc.) if desired. This allows one to efficiently generate random networks with similar properties as an observed network, scalable up to sparse graphs consisting of millions of nodes. Empirical evaluation demonstrates its competitiveness in terms of accuracy with state-of-the-art methods for link prediction and network reconstruction.