A Systematic Evaluation of Node Embedding Robustness

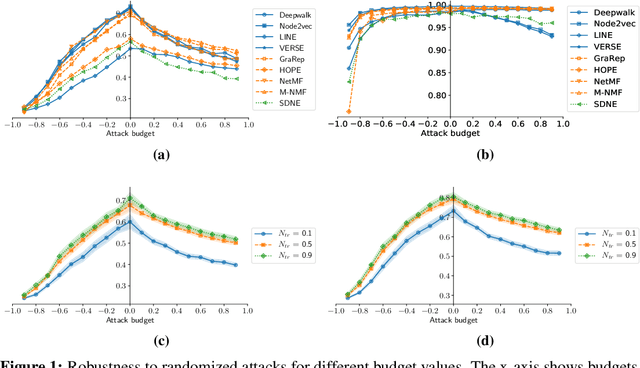
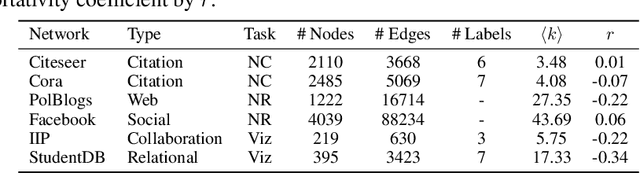
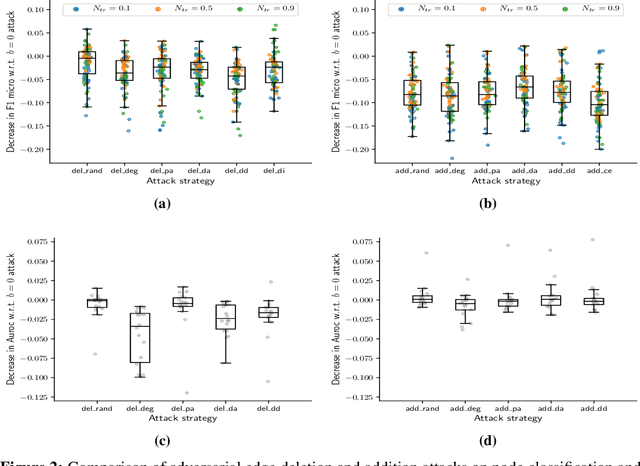
Node embedding methods map network nodes to low dimensional vectors that can be subsequently used in a variety of downstream prediction tasks. The popularity of these methods has significantly increased in recent years, yet, their robustness to perturbations of the input data is still poorly understood. In this paper, we assess the empirical robustness of node embedding models to random and adversarial poisoning attacks. Our systematic evaluation covers representative embedding methods based on Skip-Gram, matrix factorization, and deep neural networks. We compare edge addition, deletion and rewiring strategies computed using network properties as well as node labels. We also investigate the effect of label homophily and heterophily on robustness. We report qualitative results via embedding visualization and quantitative results in terms of downstream node classification and network reconstruction performances. We found that node classification suffers from higher performance degradation as opposed to network reconstruction, and that degree-based and label-based attacks are on average the most damaging.

CSNE: Conditional Signed Network Embedding

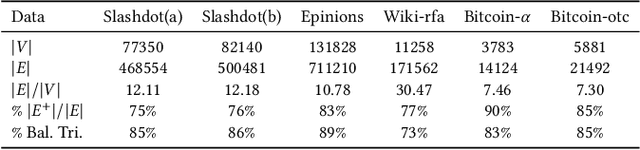
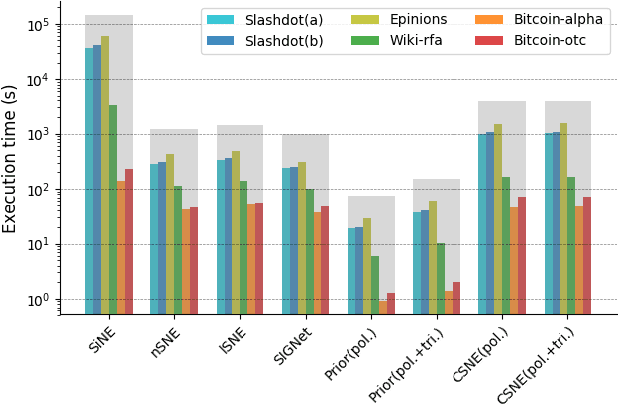
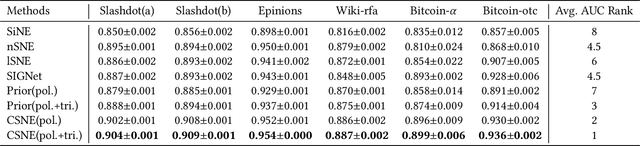
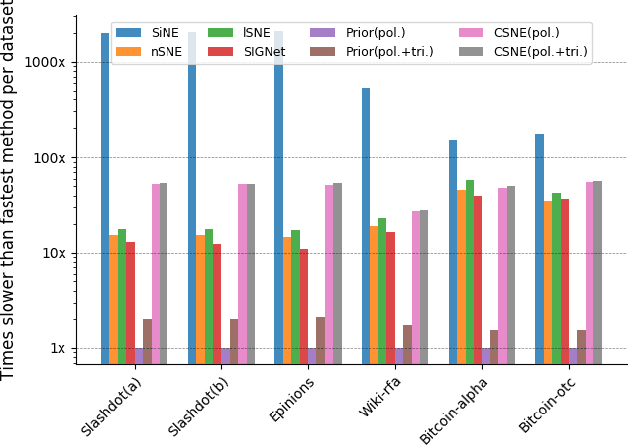
Signed networks are mathematical structures that encode positive and negative relations between entities such as friend/foe or trust/distrust. Recently, several papers studied the construction of useful low-dimensional representations (embeddings) of these networks for the prediction of missing relations or signs. Existing embedding methods for sign prediction generally enforce different notions of status or balance theories in their optimization function. These theories, however, are often inaccurate or incomplete, which negatively impacts method performance. In this context, we introduce conditional signed network embedding (CSNE). Our probabilistic approach models structural information about the signs in the network separately from fine-grained detail. Structural information is represented in the form of a prior, while the embedding itself is used for capturing fine-grained information. These components are then integrated in a rigorous manner. CSNE's accuracy depends on the existence of sufficiently powerful structural priors for modelling signed networks, currently unavailable in the literature. Thus, as a second main contribution, which we find to be highly valuable in its own right, we also introduce a novel approach to construct priors based on the Maximum Entropy (MaxEnt) principle. These priors can model the \emph{polarity} of nodes (degree to which their links are positive) as well as signed \emph{triangle counts} (a measure of the degree structural balance holds to in a network). Experiments on a variety of real-world networks confirm that CSNE outperforms the state-of-the-art on the task of sign prediction. Moreover, the MaxEnt priors on their own, while less accurate than full CSNE, achieve accuracies competitive with the state-of-the-art at very limited computational cost, thus providing an excellent runtime-accuracy trade-off in resource-constrained situations.

Network Representation Learning for Link Prediction: Are we improving upon simple heuristics?

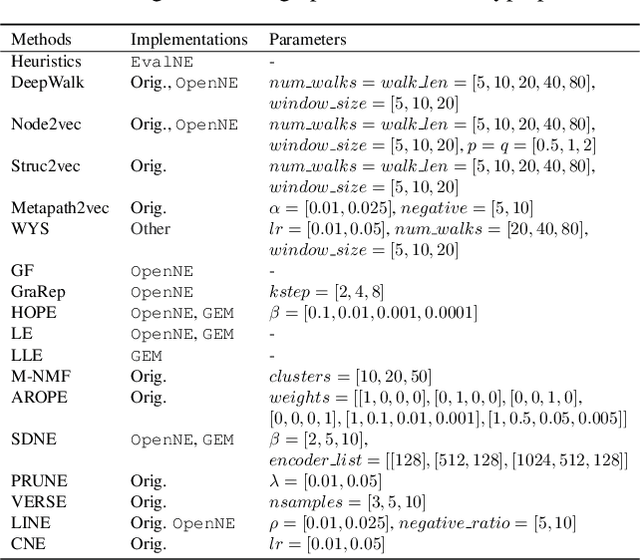
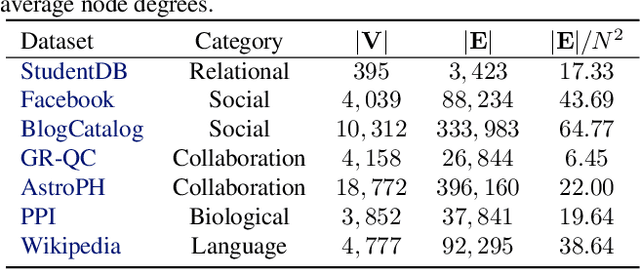
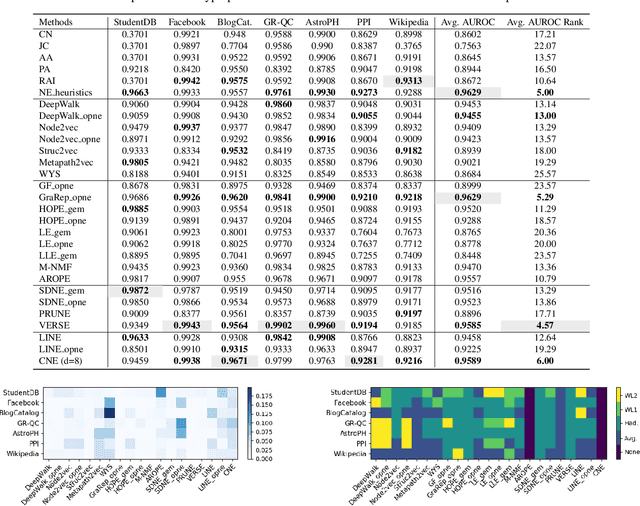
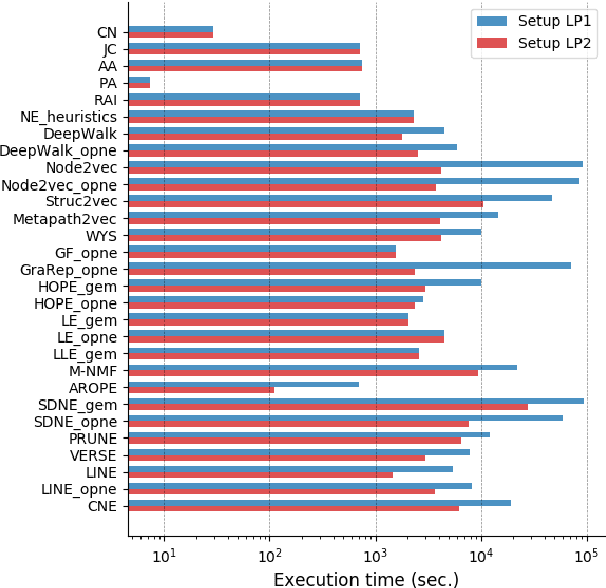
Network representation learning has become an active research area in recent years with many new methods showcasing their performance on downstream prediction tasks such as Link Prediction. Despite the efforts of the community to ensure reproducibility of research by providing method implementations, important issues remain. The complexity of the evaluation pipelines and abundance of design choices have led to difficulties in quantifying the progress in the field and identifying the state-of-the-art. In this work, we analyse 17 network embedding methods on 7 real-world datasets and find, using a consistent evaluation pipeline, only thin progress over the recent years. Also, many embedding methods are outperformed by simple heuristics. Finally, we discuss how standardized evaluation tools can repair this situation and boost progress in this field.

Scalable Dyadic Independence Models with Local and Global Constraints

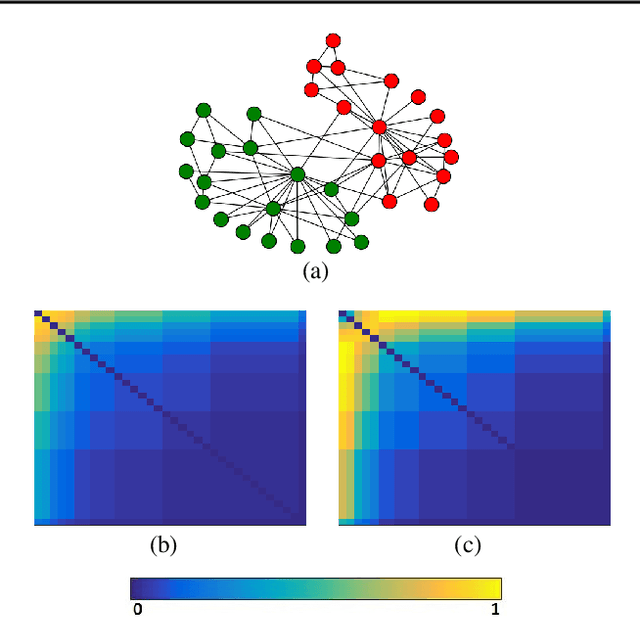
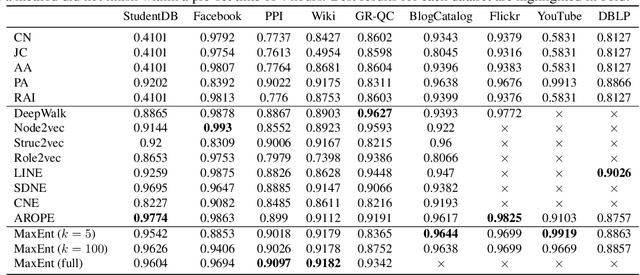
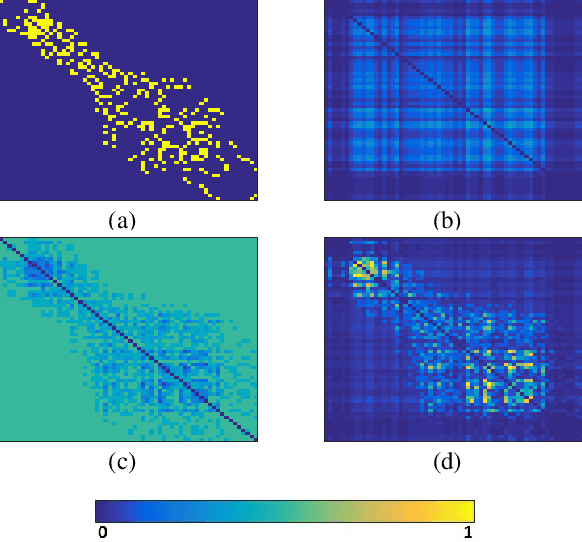
An important challenge in the field of exponential random graphs (ERGs) is the fitting of non-trivial ERGs on large networks. By utilizing matrix block-approximation techniques, we propose an approximative framework to such non-trivial ERGs that result in dyadic independence (i.e., edge independent) models, while being able to meaningfully model local information (degrees) as well as global information (clustering coefficient, assortativity, etc.) if desired. This allows one to efficiently generate random networks with similar properties as an observed network, scalable up to sparse graphs consisting of millions of nodes. Empirical evaluation demonstrates its competitiveness in terms of accuracy with state-of-the-art methods for link prediction and network reconstruction.

Semi-supervised Learning in Network-Structured Data via Total Variation Minimization

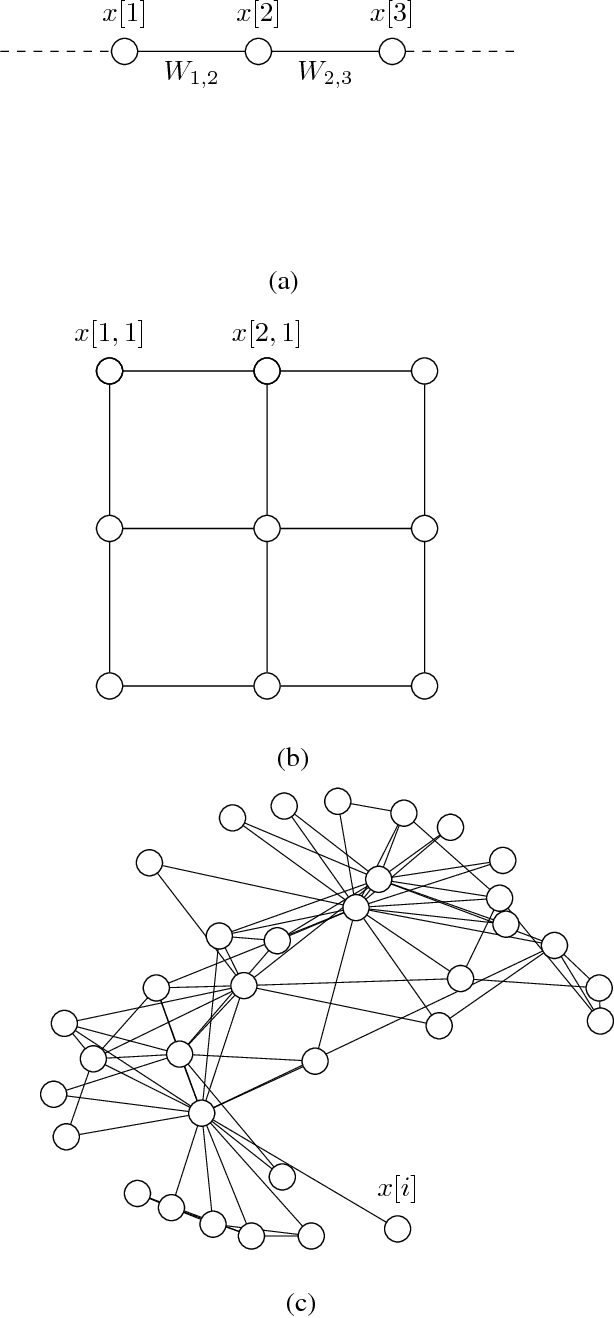
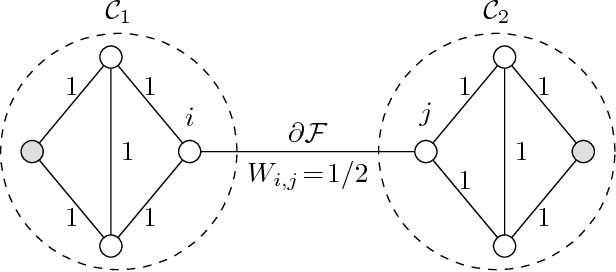
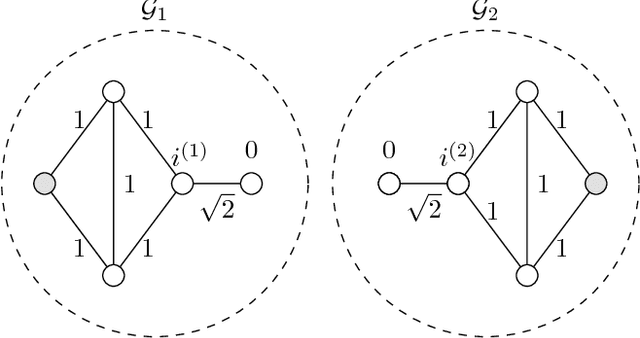
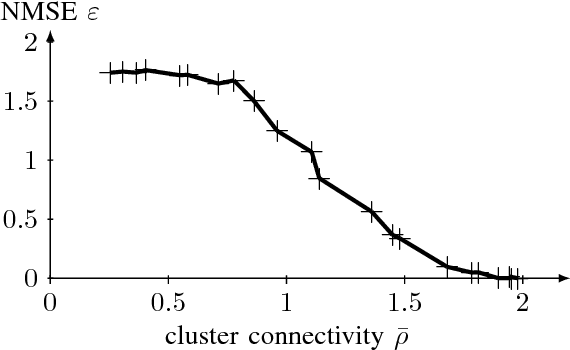
We propose and analyze a method for semi-supervised learning from partially-labeled network-structured data. Our approach is based on a graph signal recovery interpretation under a clustering hypothesis that labels of data points belonging to the same well-connected subset (cluster) are similar valued. This lends naturally to learning the labels by total variation (TV) minimization, which we solve by applying a recently proposed primal-dual method for non-smooth convex optimization. The resulting algorithm allows for a highly scalable implementation using message passing over the underlying empirical graph, which renders the algorithm suitable for big data applications. By applying tools of compressed sensing, we derive a sufficient condition on the underlying network structure such that TV minimization recovers clusters in the empirical graph of the data. In particular, we show that the proposed primal-dual method amounts to maximizing network flows over the empirical graph of the dataset. Moreover, the learning accuracy of the proposed algorithm is linked to the set of network flows between data points having known labels. The effectiveness and scalability of our approach is verified by numerical experiments.

When is Network Lasso Accurate?

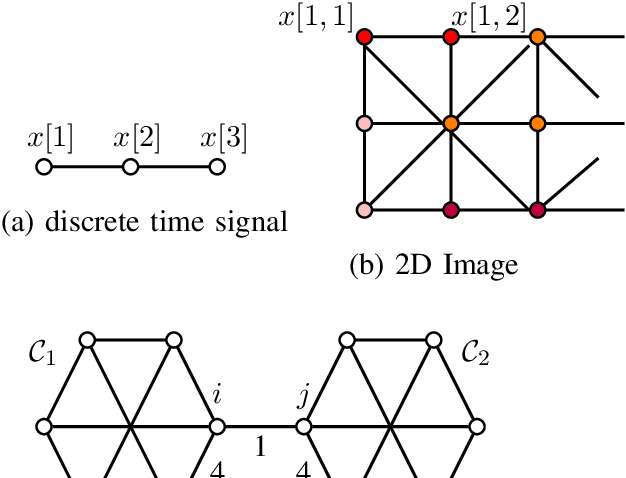
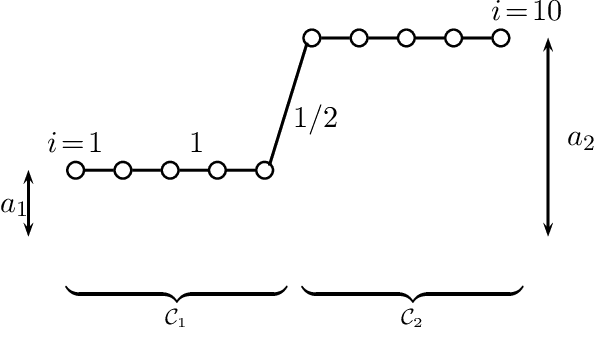
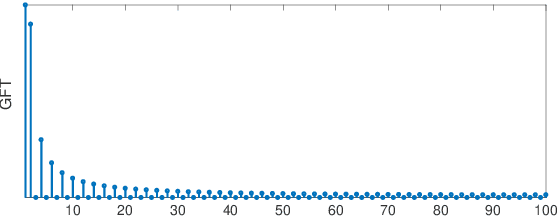
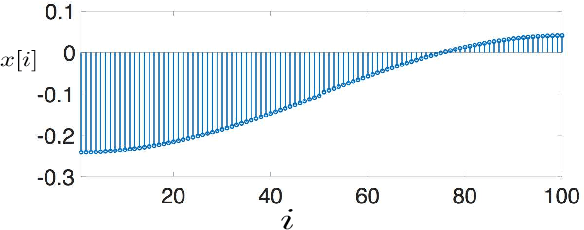
The "least absolute shrinkage and selection operator" (Lasso) method has been adapted recently for networkstructured datasets. In particular, this network Lasso method allows to learn graph signals from a small number of noisy signal samples by using the total variation of a graph signal for regularization. While efficient and scalable implementations of the network Lasso are available, only little is known about the conditions on the underlying network structure which ensure network Lasso to be accurate. By leveraging concepts of compressed sensing, we address this gap and derive precise conditions on the underlying network topology and sampling set which guarantee the network Lasso for a particular loss function to deliver an accurate estimate of the entire underlying graph signal. We also quantify the error incurred by network Lasso in terms of two constants which reflect the connectivity of the sampled nodes.

Semi-Supervised Learning via Sparse Label Propagation

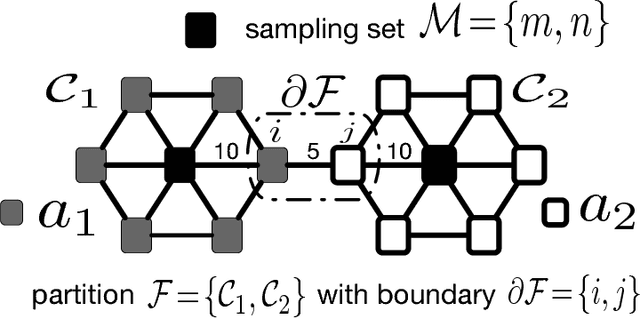
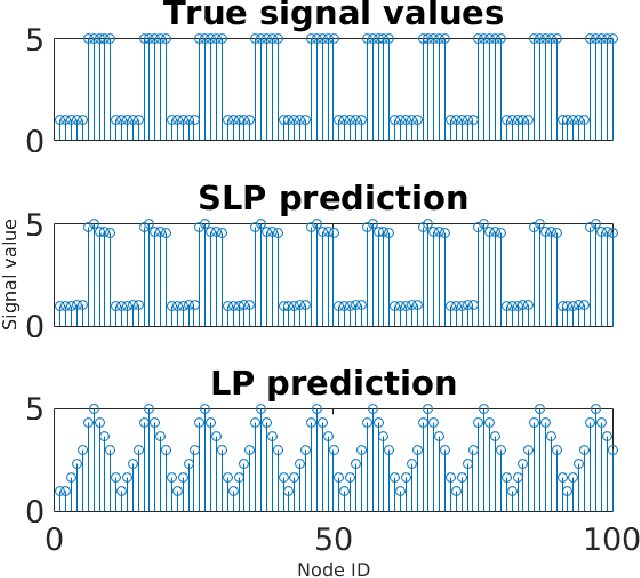
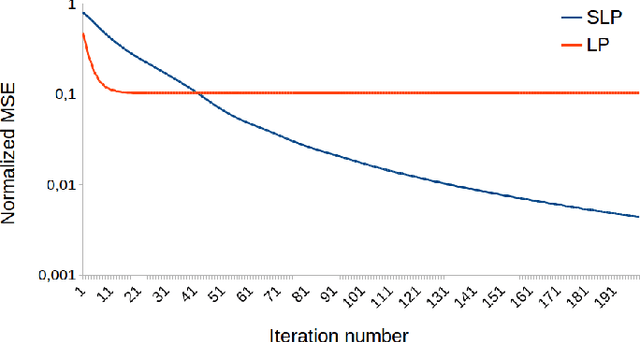
This work proposes a novel method for semi-supervised learning from partially labeled massive network-structured datasets, i.e., big data over networks. We model the underlying hypothesis, which relates data points to labels, as a graph signal, defined over some graph (network) structure intrinsic to the dataset. Following the key principle of supervised learning, i.e., similar inputs yield similar outputs, we require the graph signals induced by labels to have small total variation. Accordingly, we formulate the problem of learning the labels of data points as a non-smooth convex optimization problem which amounts to balancing between the empirical loss, i.e., the discrepancy with some partially available label information, and the smoothness quantified by the total variation of the learned graph signal. We solve this optimization problem by appealing to a recently proposed preconditioned variant of the popular primal-dual method by Pock and Chambolle, which results in a sparse label propagation algorithm. This learning algorithm allows for a highly scalable implementation as message passing over the underlying data graph. By applying concepts of compressed sensing to the learning problem, we are also able to provide a transparent sufficient condition on the underlying network structure such that accurate learning of the labels is possible. We also present an implementation of the message passing formulation allows for a highly scalable implementation in big data frameworks.

Scalable Semi-Supervised Learning over Networks using Nonsmooth Convex Optimization

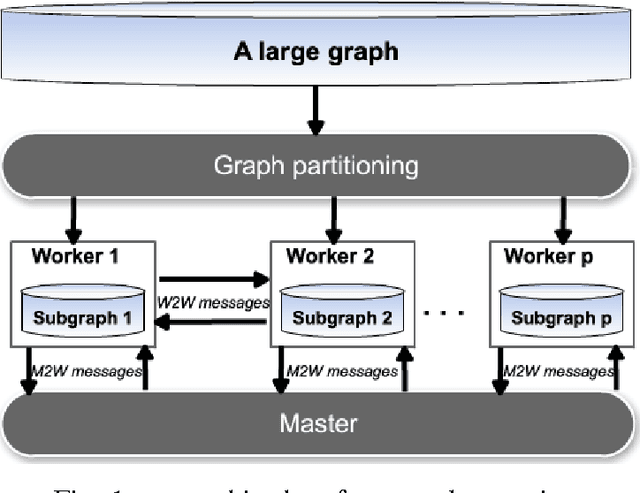
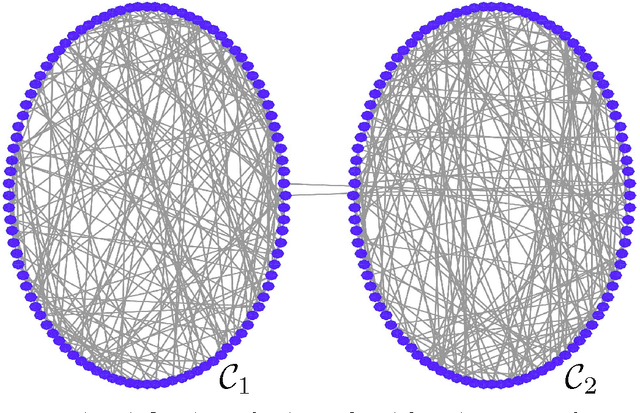
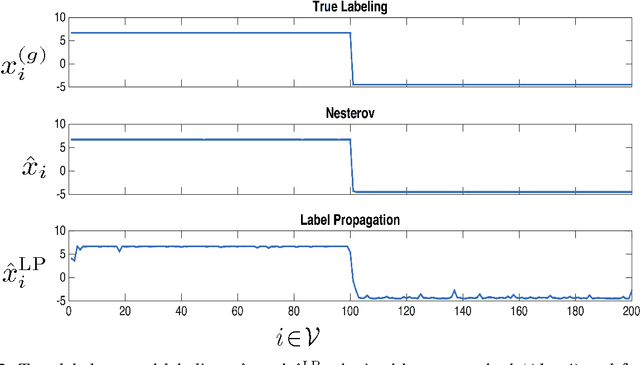
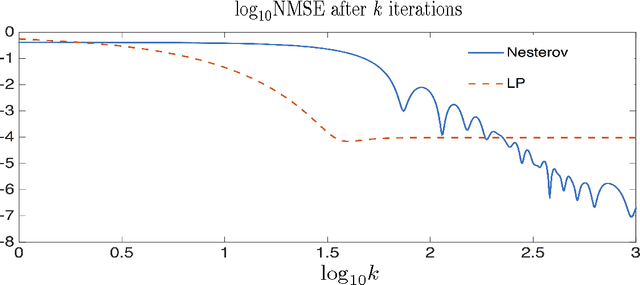
We propose a scalable method for semi-supervised (transductive) learning from massive network-structured datasets. Our approach to semi-supervised learning is based on representing the underlying hypothesis as a graph signal with small total variation. Requiring a small total variation of the graph signal representing the underlying hypothesis corresponds to the central smoothness assumption that forms the basis for semi-supervised learning, i.e., input points forming clusters have similar output values or labels. We formulate the learning problem as a nonsmooth convex optimization problem which we solve by appealing to Nesterovs optimal first-order method for nonsmooth optimization. We also provide a message passing formulation of the learning method which allows for a highly scalable implementation in big data frameworks.