Engineering Trustworthy AI: A Developer Guide for Empirical Risk Minimization

AI systems increasingly shape critical decisions across personal and societal domains. While empirical risk minimization (ERM) drives much of the AI success, it typically prioritizes accuracy over trustworthiness, often resulting in biases, opacity, and other adverse effects. This paper discusses how key requirements for trustworthy AI can be translated into design choices for the components of ERM. We hope to provide actionable guidance for building AI systems that meet emerging standards for trustworthiness of AI.

Personalized Federated Learning via Active Sampling

Consider a collection of data generators which could represent, e.g., humans equipped with a smart-phone or wearables. We want to train a personalized (or tailored) model for each data generator even if they provide only small local datasets. The available local datasets might fail to provide sufficient statistical power to train high-dimensional models (such as deep neural networks) effectively. One possible solution is to identify similar data generators and pool their local datasets to obtain a sufficiently large training set. This paper proposes a novel method for sequentially identifying similar (or relevant) data generators. Our method is similar in spirit to active sampling methods but does not require exchange of raw data. Indeed, our method evaluates the relevance of a data generator by evaluating the effect of a gradient step using its local dataset. This evaluation can be performed in a privacy-friendly fashion without sharing raw data. We extend this method to non-parametric models by a suitable generalization of the gradient step to update a hypothesis using the local dataset provided by a data generator.

Moreau Envelope ADMM for Decentralized Weakly Convex Optimization

This paper proposes a proximal variant of the alternating direction method of multipliers (ADMM) for distributed optimization. Although the current versions of ADMM algorithm provide promising numerical results in producing solutions that are close to optimal for many convex and non-convex optimization problems, it remains unclear if they can converge to a stationary point for weakly convex and locally non-smooth functions. Through our analysis using the Moreau envelope function, we demonstrate that MADM can indeed converge to a stationary point under mild conditions. Our analysis also includes computing the bounds on the amount of change in the dual variable update step by relating the gradient of the Moreau envelope function to the proximal function. Furthermore, the results of our numerical experiments indicate that our method is faster and more robust than widely-used approaches.

Rethinking Drone-Based Search and Rescue with Aerial Person Detection

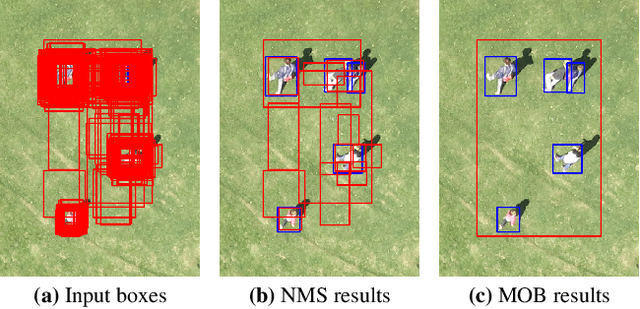
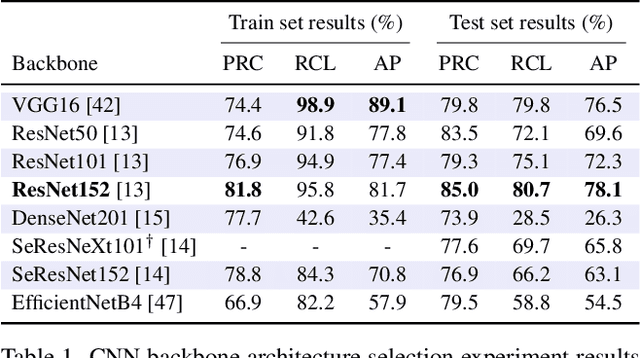
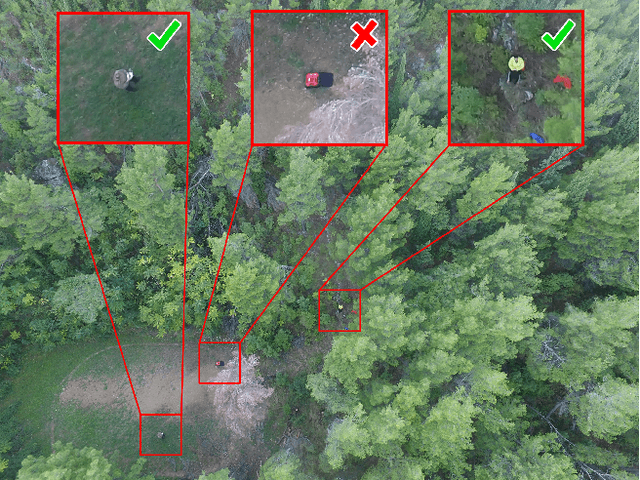
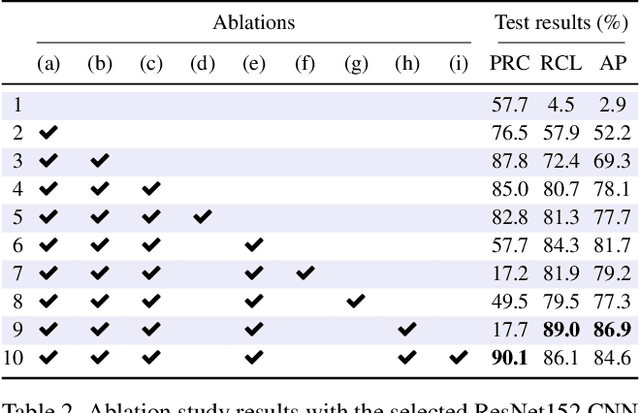
The visual inspection of aerial drone footage is an integral part of land search and rescue (SAR) operations today. Since this inspection is a slow, tedious and error-prone job for humans, we propose a novel deep learning algorithm to automate this aerial person detection (APD) task. We experiment with model architecture selection, online data augmentation, transfer learning, image tiling and several other techniques to improve the test performance of our method. We present the novel Aerial Inspection RetinaNet (AIR) algorithm as the combination of these contributions. The AIR detector demonstrates state-of-the-art performance on a commonly used SAR test data set in terms of both precision (~21 percentage point increase) and speed. In addition, we provide a new formal definition for the APD problem in SAR missions. That is, we propose a novel evaluation scheme that ranks detectors in terms of real-world SAR localization requirements. Finally, we propose a novel postprocessing method for robust, approximate object localization: the merging of overlapping bounding boxes (MOB) algorithm. This final processing stage used in the AIR detector significantly improves its performance and usability in the face of real-world aerial SAR missions.

Networked Federated Multi-Task Learning

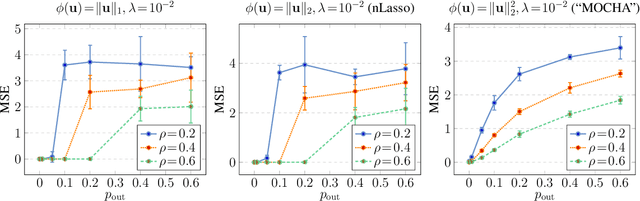
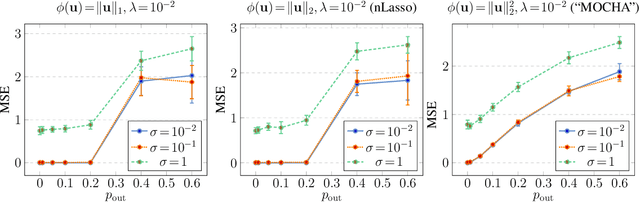
Many important application domains generate distributed collections of heterogeneous local datasets. These local datasets are often related via an intrinsic network structure that arises from domain-specific notions of similarity between local datasets. Different notions of similarity are induced by spatiotemporal proximity, statistical dependencies, or functional relations. We use this network structure to adaptively pool similar local datasets into nearly homogenous training sets for learning tailored models. Our main conceptual contribution is to formulate networked federated learning using the concept of generalized total variation (GTV) minimization as a regularizer. This formulation is highly flexible and can be combined with almost any parametric model including Lasso or deep neural networks. We unify and considerably extend some well-known approaches to federated multi-task learning. Our main algorithmic contribution is a novel federated learning algorithm that is well suited for distributed computing environments such as edge computing over wireless networks. This algorithm is robust against model misspecification and numerical errors arising from limited computational resources including processing time or wireless channel bandwidth. As our main technical contribution, we offer precise conditions on the local models as well on their network structure such that our algorithm learns nearly optimal local models. Our analysis reveals an interesting interplay between the (information-) geometry of local models and the (cluster-) geometry of their network.

Local Graph Clustering with Network Lasso

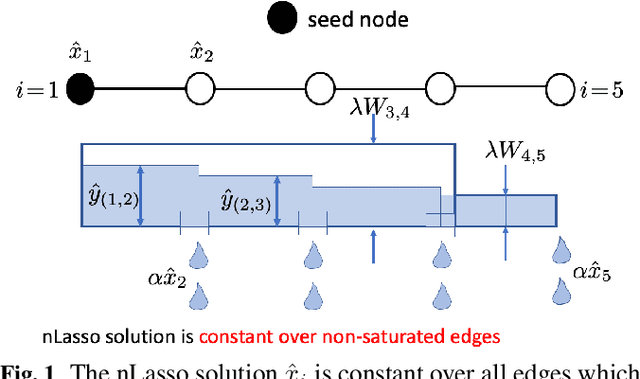
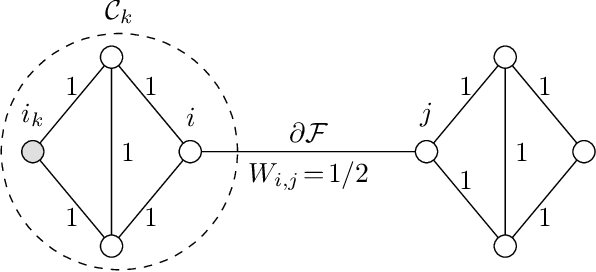
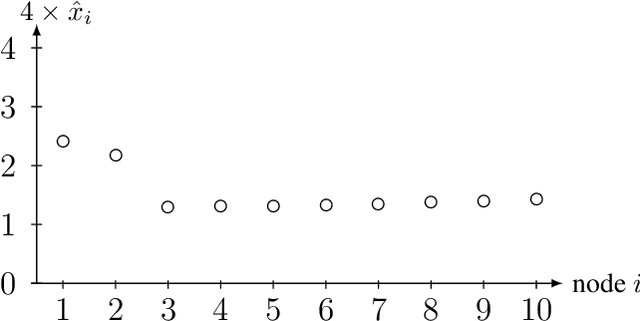
We study the statistical and computational properties of a network Lasso method for local graph clustering. The clusters delivered by nLasso can be characterized elegantly via network flows between cluster boundary and seed nodes. While spectral clustering methods are guided by a minimization of the graph Laplacian quadratic form, nLasso minimizes the total variation of cluster indicator signals. As demonstrated theoretically and numerically, nLasso methods can handle very sparse clusters (chain-like) which are difficult for spectral clustering. We also verify that a primal-dual method for non-smooth optimization allows to approximate nLasso solutions with optimal worst-case convergence rate.

An Information-Theoretic Approach to Personalized Explainable Machine Learning

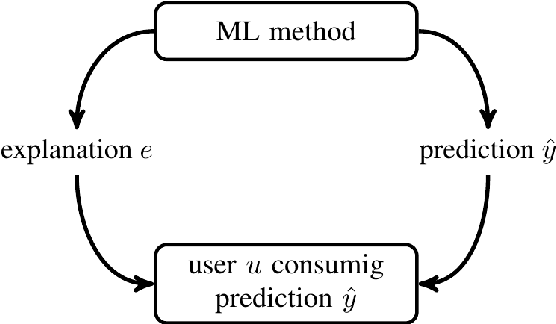
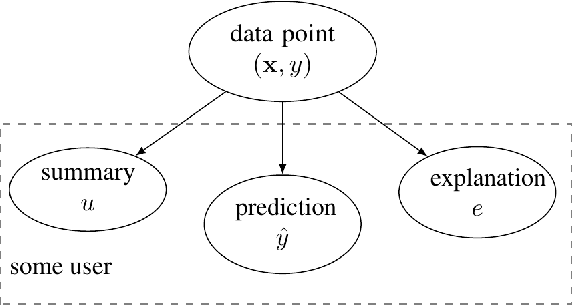
Automated decision making is used routinely throughout our everyday life. Recommender systems decide which jobs, movies, or other user profiles might be interesting to us. Spell checkers help us to make good use of language. Fraud detection systems decide if a credit card transactions should be verified more closely. Many of these decision making systems use machine learning methods that fit complex models to massive datasets. The successful deployment of machine learning (ML) methods to many (critical) application domains crucially depends on its explainability. Indeed, humans have a strong desire to get explanations that resolve the uncertainty about experienced phenomena like the predictions and decisions obtained from ML methods. Explainable ML is challenging since explanations must be tailored (personalized) to individual users with varying backgrounds. Some users might have received university-level education in ML, while other users might have no formal training in linear algebra. Linear regression with few features might be perfectly interpretable for the first group but might be considered a black-box by the latter. We propose a simple probabilistic model for the predictions and user knowledge. This model allows to study explainable ML using information theory. Explaining is here considered as the task of reducing the "surprise" incurred by a prediction. We quantify the effect of an explanation by the conditional mutual information between the explanation and prediction, given the user background.

Basic Principles of Clustering Methods

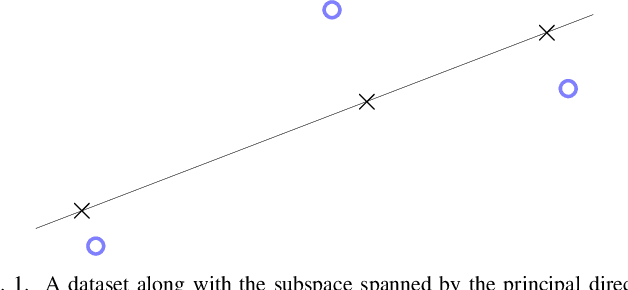
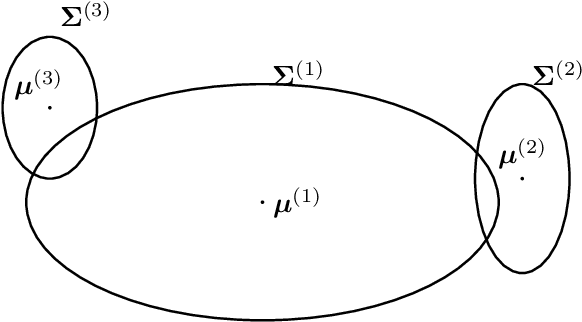
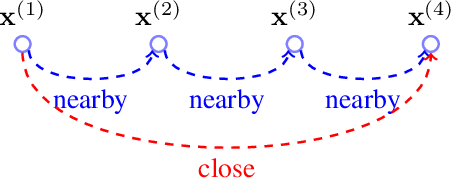
Clustering methods group a set of data points into a few coherent groups or clusters of similar data points. As an example, consider clustering pixels in an image (or video) if they belong to the same object. Different clustering methods are obtained by using different notions of similarity and different representations of data points.

Clustering in Partially Labeled Stochastic Block Models via Total Variation Minimization

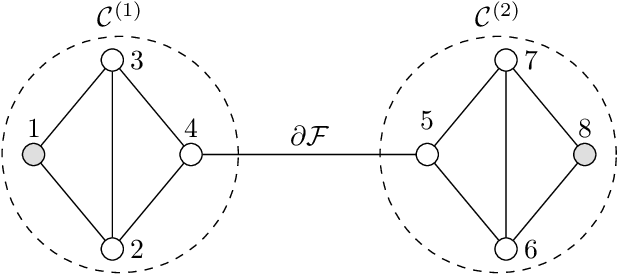
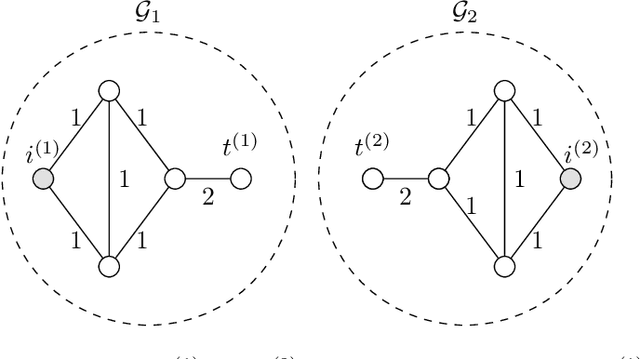
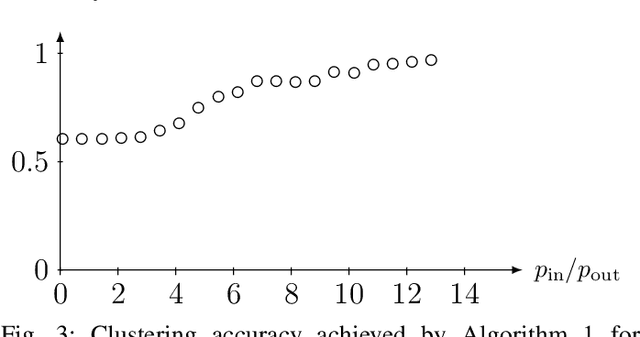
A main task in data analysis is to organize data points into coherent groups or clusters. The stochastic block model is a probabilistic model for the cluster structure. This model prescribes different probabilities for the presence of edges within a cluster and between different clusters. We assume that the cluster assignments are known for at least one data point in each cluster. In such a partially labeled stochastic block model, clustering amounts to estimating the cluster assignments of the remaining data points. We study total variation minimization as a method for this clustering task. We implement the resulting clustering algorithm as a highly scalable message passing protocol. We also provide a condition on the model parameters such that total variation minimization allows for accurate clustering.

Components of Machine Learning: Binding Bits and FLOPS

Many machine learning problems and methods are combinations of three components: data, hypothesis space and loss function. Different machine learning methods are obtained as combinations of different choices for the representation of data, hypothesis space and loss function. After reviewing the mathematical structure of these three components, we discuss intrinsic trade-offs between statistical and computational properties of machine learning methods.