Federated Smoothing Proximal Gradient for Quantile Regression with Non-Convex Penalties

Distributed sensors in the internet-of-things (IoT) generate vast amounts of sparse data. Analyzing this high-dimensional data and identifying relevant predictors pose substantial challenges, especially when data is preferred to remain on the device where it was collected for reasons such as data integrity, communication bandwidth, and privacy. This paper introduces a federated quantile regression algorithm to address these challenges. Quantile regression provides a more comprehensive view of the relationship between variables than mean regression models. However, traditional approaches face difficulties when dealing with nonconvex sparse penalties and the inherent non-smoothness of the loss function. For this purpose, we propose a federated smoothing proximal gradient (FSPG) algorithm that integrates a smoothing mechanism with the proximal gradient framework, thereby enhancing both precision and computational speed. This integration adeptly handles optimization over a network of devices, each holding local data samples, making it particularly effective in federated learning scenarios. The FSPG algorithm ensures steady progress and reliable convergence in each iteration by maintaining or reducing the value of the objective function. By leveraging nonconvex penalties, such as the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD), the proposed method can identify and preserve key predictors within sparse models. Comprehensive simulations validate the robust theoretical foundations of the proposed algorithm and demonstrate improved estimation precision and reliable convergence.

Decentralized Smoothing ADMM for Quantile Regression with Non-Convex Sparse Penalties

In the rapidly evolving internet-of-things (IoT) ecosystem, effective data analysis techniques are crucial for handling distributed data generated by sensors. Addressing the limitations of existing methods, such as the sub-gradient approach, which fails to distinguish between active and non-active coefficients effectively, this paper introduces the decentralized smoothing alternating direction method of multipliers (DSAD) for penalized quantile regression. Our method leverages non-convex sparse penalties like the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD), improving the identification and retention of significant predictors. DSAD incorporates a total variation norm within a smoothing ADMM framework, achieving consensus among distributed nodes and ensuring uniform model performance across disparate data sources. This approach overcomes traditional convergence challenges associated with non-convex penalties in decentralized settings. We present theoretical proofs and extensive simulation results to validate the effectiveness of the DSAD, demonstrating its superiority in achieving reliable convergence and enhancing estimation accuracy compared with prior methods.

Smoothing ADMM for Sparse-Penalized Quantile Regression with Non-Convex Penalties

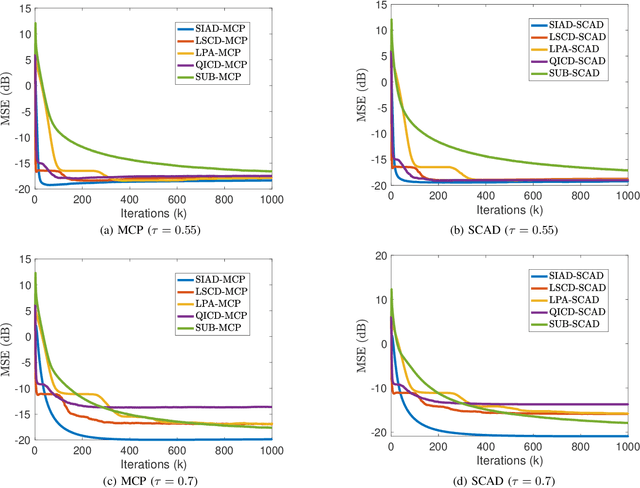
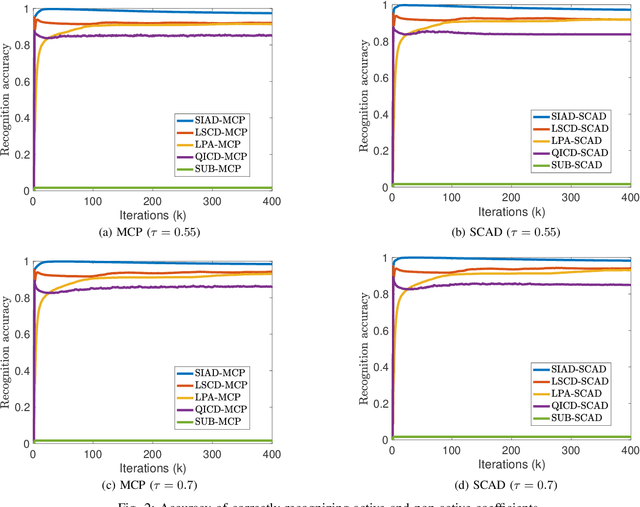
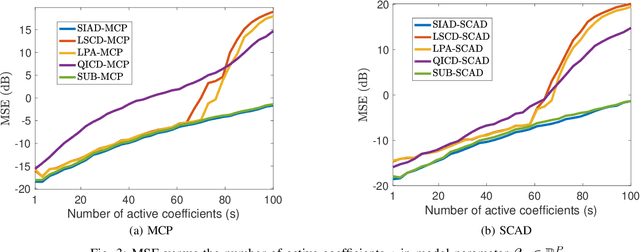
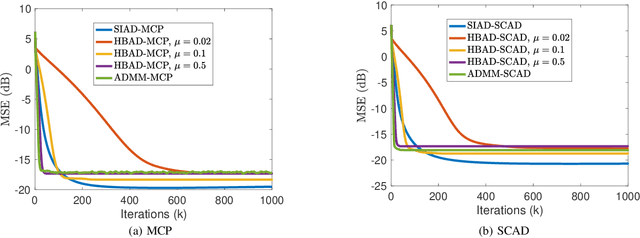
This paper investigates quantile regression in the presence of non-convex and non-smooth sparse penalties, such as the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD). The non-smooth and non-convex nature of these problems often leads to convergence difficulties for many algorithms. While iterative techniques like coordinate descent and local linear approximation can facilitate convergence, the process is often slow. This sluggish pace is primarily due to the need to run these approximation techniques until full convergence at each step, a requirement we term as a \emph{secondary convergence iteration}. To accelerate the convergence speed, we employ the alternating direction method of multipliers (ADMM) and introduce a novel single-loop smoothing ADMM algorithm with an increasing penalty parameter, named SIAD, specifically tailored for sparse-penalized quantile regression. We first delve into the convergence properties of the proposed SIAD algorithm and establish the necessary conditions for convergence. Theoretically, we confirm a convergence rate of $o\big({k^{-\frac{1}{4}}}\big)$ for the sub-gradient bound of augmented Lagrangian. Subsequently, we provide numerical results to showcase the effectiveness of the SIAD algorithm. Our findings highlight that the SIAD method outperforms existing approaches, providing a faster and more stable solution for sparse-penalized quantile regression.

Robust Networked Federated Learning for Localization

This paper addresses the problem of localization, which is inherently non-convex and non-smooth in a federated setting where the data is distributed across a multitude of devices. Due to the decentralized nature of federated environments, distributed learning becomes essential for scalability and adaptability. Moreover, these environments are often plagued by outlier data, which presents substantial challenges to conventional methods, particularly in maintaining estimation accuracy and ensuring algorithm convergence. To mitigate these challenges, we propose a method that adopts an $L_1$-norm robust formulation within a distributed sub-gradient framework, explicitly designed to handle these obstacles. Our approach addresses the problem in its original form, without resorting to iterative simplifications or approximations, resulting in enhanced computational efficiency and improved estimation accuracy. We demonstrate that our method converges to a stationary point, highlighting its effectiveness and reliability. Through numerical simulations, we confirm the superior performance of our approach, notably in outlier-rich environments, which surpasses existing state-of-the-art localization methods.

Moreau Envelope ADMM for Decentralized Weakly Convex Optimization

This paper proposes a proximal variant of the alternating direction method of multipliers (ADMM) for distributed optimization. Although the current versions of ADMM algorithm provide promising numerical results in producing solutions that are close to optimal for many convex and non-convex optimization problems, it remains unclear if they can converge to a stationary point for weakly convex and locally non-smooth functions. Through our analysis using the Moreau envelope function, we demonstrate that MADM can indeed converge to a stationary point under mild conditions. Our analysis also includes computing the bounds on the amount of change in the dual variable update step by relating the gradient of the Moreau envelope function to the proximal function. Furthermore, the results of our numerical experiments indicate that our method is faster and more robust than widely-used approaches.

Structure Learning of Sparse GGMs over Multiple Access Networks

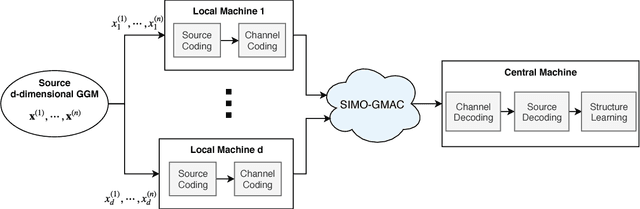
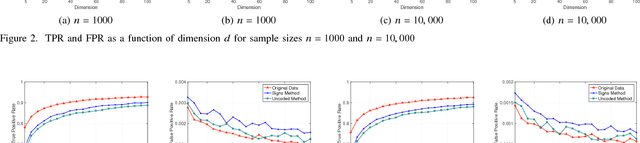
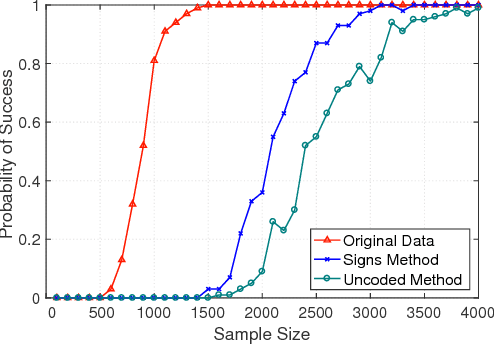
A central machine is interested in estimating the underlying structure of a sparse Gaussian Graphical Model (GGM) from datasets distributed across multiple local machines. The local machines can communicate with the central machine through a wireless multiple access channel. In this paper, we are interested in designing effective strategies where reliable learning is feasible under power and bandwidth limitations. Two approaches are proposed: Signs and Uncoded methods. In Signs method, the local machines quantize their data into binary vectors and an optimal channel coding scheme is used to reliably send the vectors to the central machine where the structure is learned from the received data. In Uncoded method, data symbols are scaled and transmitted through the channel. The central machine uses the received noisy symbols to recover the structure. Theoretical results show that both methods can recover the structure with high probability for large enough sample size. Experimental results indicate the superiority of Signs method over Uncoded method under several circumstances.