Federated Smoothing ADMM for Localization

This paper addresses the challenge of localization in federated settings, which are characterized by distributed data, non-convexity, and non-smoothness. To tackle the scalability and outlier issues inherent in such environments, we propose a robust algorithm that employs an $\ell_1$-norm formulation within a novel federated ADMM framework. This approach addresses the problem by integrating an iterative smooth approximation for the total variation consensus term and employing a Moreau envelope approximation for the convex function that appears in a subtracted form. This transformation ensures that the problem is smooth and weakly convex in each iteration, which results in enhanced computational efficiency and improved estimation accuracy. The proposed algorithm supports asynchronous updates and multiple client updates per iteration, which ensures its adaptability to real-world federated systems. To validate the reliability of the proposed algorithm, we show that the method converges to a stationary point, and numerical simulations highlight its superior performance in convergence speed and outlier resilience compared to existing state-of-the-art localization methods.

Smoothing ADMM for Non-convex and Non-smooth Hierarchical Federated Learning

This paper presents a hierarchical federated learning (FL) framework that extends the alternating direction method of multipliers (ADMM) with smoothing techniques, tailored for non-convex and non-smooth objectives. Unlike traditional hierarchical FL methods, our approach supports asynchronous updates and multiple updates per iteration, enhancing adaptability to heterogeneous data and system settings. Additionally, we introduce a flexible mechanism to leverage diverse regularization functions at each layer, allowing customization to the specific prior information within each cluster and accommodating (possibly) non-smooth penalty objectives. Depending on the learning goal, the framework supports both consensus and personalization: the total variation norm can be used to enforce consensus across layers, while non-convex penalties such as minimax concave penalty (MCP) or smoothly clipped absolute deviation (SCAD) enable personalized learning. Experimental results demonstrate the superior convergence rates and accuracy of our method compared to conventional approaches, underscoring its robustness and versatility for a wide range of FL scenarios.

Federated Smoothing Proximal Gradient for Quantile Regression with Non-Convex Penalties

Distributed sensors in the internet-of-things (IoT) generate vast amounts of sparse data. Analyzing this high-dimensional data and identifying relevant predictors pose substantial challenges, especially when data is preferred to remain on the device where it was collected for reasons such as data integrity, communication bandwidth, and privacy. This paper introduces a federated quantile regression algorithm to address these challenges. Quantile regression provides a more comprehensive view of the relationship between variables than mean regression models. However, traditional approaches face difficulties when dealing with nonconvex sparse penalties and the inherent non-smoothness of the loss function. For this purpose, we propose a federated smoothing proximal gradient (FSPG) algorithm that integrates a smoothing mechanism with the proximal gradient framework, thereby enhancing both precision and computational speed. This integration adeptly handles optimization over a network of devices, each holding local data samples, making it particularly effective in federated learning scenarios. The FSPG algorithm ensures steady progress and reliable convergence in each iteration by maintaining or reducing the value of the objective function. By leveraging nonconvex penalties, such as the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD), the proposed method can identify and preserve key predictors within sparse models. Comprehensive simulations validate the robust theoretical foundations of the proposed algorithm and demonstrate improved estimation precision and reliable convergence.

Decentralized Smoothing ADMM for Quantile Regression with Non-Convex Sparse Penalties

In the rapidly evolving internet-of-things (IoT) ecosystem, effective data analysis techniques are crucial for handling distributed data generated by sensors. Addressing the limitations of existing methods, such as the sub-gradient approach, which fails to distinguish between active and non-active coefficients effectively, this paper introduces the decentralized smoothing alternating direction method of multipliers (DSAD) for penalized quantile regression. Our method leverages non-convex sparse penalties like the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD), improving the identification and retention of significant predictors. DSAD incorporates a total variation norm within a smoothing ADMM framework, achieving consensus among distributed nodes and ensuring uniform model performance across disparate data sources. This approach overcomes traditional convergence challenges associated with non-convex penalties in decentralized settings. We present theoretical proofs and extensive simulation results to validate the effectiveness of the DSAD, demonstrating its superiority in achieving reliable convergence and enhancing estimation accuracy compared with prior methods.

Distributed Maximum Consensus over Noisy Links

We introduce a distributed algorithm, termed noise-robust distributed maximum consensus (RD-MC), for estimating the maximum value within a multi-agent network in the presence of noisy communication links. Our approach entails redefining the maximum consensus problem as a distributed optimization problem, allowing a solution using the alternating direction method of multipliers. Unlike existing algorithms that rely on multiple sets of noise-corrupted estimates, RD-MC employs a single set, enhancing both robustness and efficiency. To further mitigate the effects of link noise and improve robustness, we apply moving averaging to the local estimates. Through extensive simulations, we demonstrate that RD-MC is significantly more robust to communication link noise compared to existing maximum-consensus algorithms.

Privacy-Preserving Distributed Nonnegative Matrix Factorization

Nonnegative matrix factorization (NMF) is an effective data representation tool with numerous applications in signal processing and machine learning. However, deploying NMF in a decentralized manner over ad-hoc networks introduces privacy concerns due to the conventional approach of sharing raw data among network agents. To address this, we propose a privacy-preserving algorithm for fully-distributed NMF that decomposes a distributed large data matrix into left and right matrix factors while safeguarding each agent's local data privacy. It facilitates collaborative estimation of the left matrix factor among agents and enables them to estimate their respective right factors without exposing raw data. To ensure data privacy, we secure information exchanges between neighboring agents utilizing the Paillier cryptosystem, a probabilistic asymmetric algorithm for public-key cryptography that allows computations on encrypted data without decryption. Simulation results conducted on synthetic and real-world datasets demonstrate the effectiveness of the proposed algorithm in achieving privacy-preserving distributed NMF over ad-hoc networks.

Analyzing the Impact of Partial Sharing on the Resilience of Online Federated Learning Against Model Poisoning Attacks

We scrutinize the resilience of the partial-sharing online federated learning (PSO-Fed) algorithm against model-poisoning attacks. PSO-Fed reduces the communication load by enabling clients to exchange only a fraction of their model estimates with the server at each update round. Partial sharing of model estimates also enhances the robustness of the algorithm against model-poisoning attacks. To gain better insights into this phenomenon, we analyze the performance of the PSO-Fed algorithm in the presence of Byzantine clients, malicious actors who may subtly tamper with their local models by adding noise before sharing them with the server. Through our analysis, we demonstrate that PSO-Fed maintains convergence in both mean and mean-square senses, even under the strain of model-poisoning attacks. We further derive the theoretical mean square error (MSE) of PSO-Fed, linking it to various parameters such as stepsize, attack probability, number of Byzantine clients, client participation rate, partial-sharing ratio, and noise variance. We also show that there is a non-trivial optimal stepsize for PSO-Fed when faced with model-poisoning attacks. The results of our extensive numerical experiments affirm our theoretical assertions and highlight the superior ability of PSO-Fed to counteract Byzantine attacks, outperforming other related leading algorithms.

Smoothing ADMM for Sparse-Penalized Quantile Regression with Non-Convex Penalties

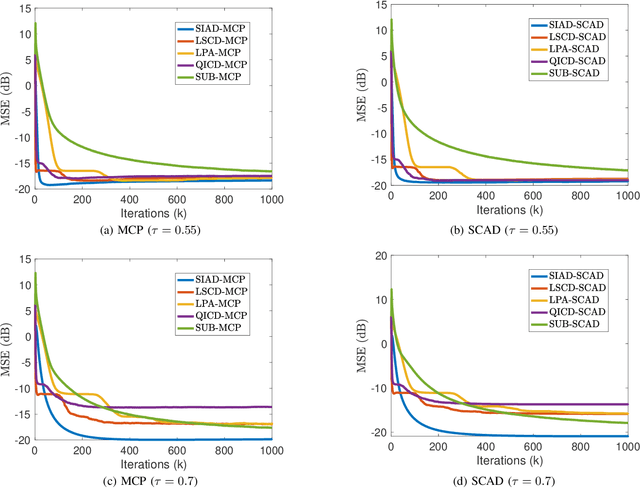
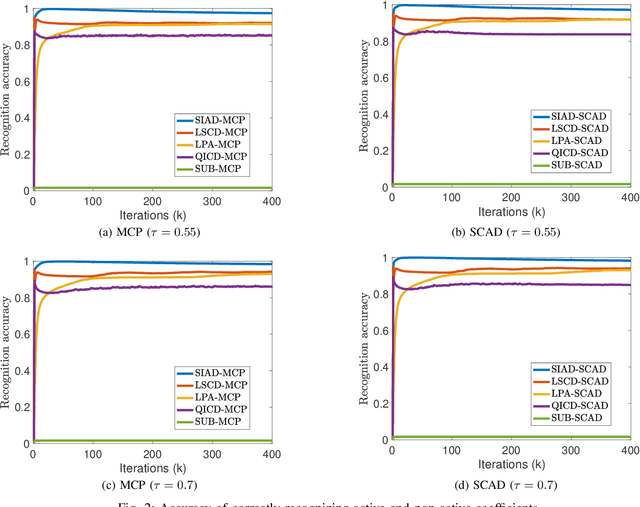
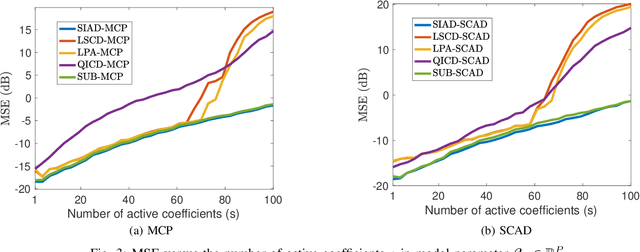
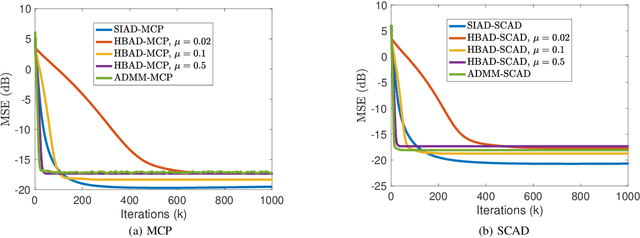
This paper investigates quantile regression in the presence of non-convex and non-smooth sparse penalties, such as the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD). The non-smooth and non-convex nature of these problems often leads to convergence difficulties for many algorithms. While iterative techniques like coordinate descent and local linear approximation can facilitate convergence, the process is often slow. This sluggish pace is primarily due to the need to run these approximation techniques until full convergence at each step, a requirement we term as a \emph{secondary convergence iteration}. To accelerate the convergence speed, we employ the alternating direction method of multipliers (ADMM) and introduce a novel single-loop smoothing ADMM algorithm with an increasing penalty parameter, named SIAD, specifically tailored for sparse-penalized quantile regression. We first delve into the convergence properties of the proposed SIAD algorithm and establish the necessary conditions for convergence. Theoretically, we confirm a convergence rate of $o\big({k^{-\frac{1}{4}}}\big)$ for the sub-gradient bound of augmented Lagrangian. Subsequently, we provide numerical results to showcase the effectiveness of the SIAD algorithm. Our findings highlight that the SIAD method outperforms existing approaches, providing a faster and more stable solution for sparse-penalized quantile regression.

Robust Networked Federated Learning for Localization

This paper addresses the problem of localization, which is inherently non-convex and non-smooth in a federated setting where the data is distributed across a multitude of devices. Due to the decentralized nature of federated environments, distributed learning becomes essential for scalability and adaptability. Moreover, these environments are often plagued by outlier data, which presents substantial challenges to conventional methods, particularly in maintaining estimation accuracy and ensuring algorithm convergence. To mitigate these challenges, we propose a method that adopts an $L_1$-norm robust formulation within a distributed sub-gradient framework, explicitly designed to handle these obstacles. Our approach addresses the problem in its original form, without resorting to iterative simplifications or approximations, resulting in enhanced computational efficiency and improved estimation accuracy. We demonstrate that our method converges to a stationary point, highlighting its effectiveness and reliability. Through numerical simulations, we confirm the superior performance of our approach, notably in outlier-rich environments, which surpasses existing state-of-the-art localization methods.

Moreau Envelope ADMM for Decentralized Weakly Convex Optimization

This paper proposes a proximal variant of the alternating direction method of multipliers (ADMM) for distributed optimization. Although the current versions of ADMM algorithm provide promising numerical results in producing solutions that are close to optimal for many convex and non-convex optimization problems, it remains unclear if they can converge to a stationary point for weakly convex and locally non-smooth functions. Through our analysis using the Moreau envelope function, we demonstrate that MADM can indeed converge to a stationary point under mild conditions. Our analysis also includes computing the bounds on the amount of change in the dual variable update step by relating the gradient of the Moreau envelope function to the proximal function. Furthermore, the results of our numerical experiments indicate that our method is faster and more robust than widely-used approaches.