Distributed Maximum Consensus over Noisy Links

We introduce a distributed algorithm, termed noise-robust distributed maximum consensus (RD-MC), for estimating the maximum value within a multi-agent network in the presence of noisy communication links. Our approach entails redefining the maximum consensus problem as a distributed optimization problem, allowing a solution using the alternating direction method of multipliers. Unlike existing algorithms that rely on multiple sets of noise-corrupted estimates, RD-MC employs a single set, enhancing both robustness and efficiency. To further mitigate the effects of link noise and improve robustness, we apply moving averaging to the local estimates. Through extensive simulations, we demonstrate that RD-MC is significantly more robust to communication link noise compared to existing maximum-consensus algorithms.

Smoothing ADMM for Sparse-Penalized Quantile Regression with Non-Convex Penalties

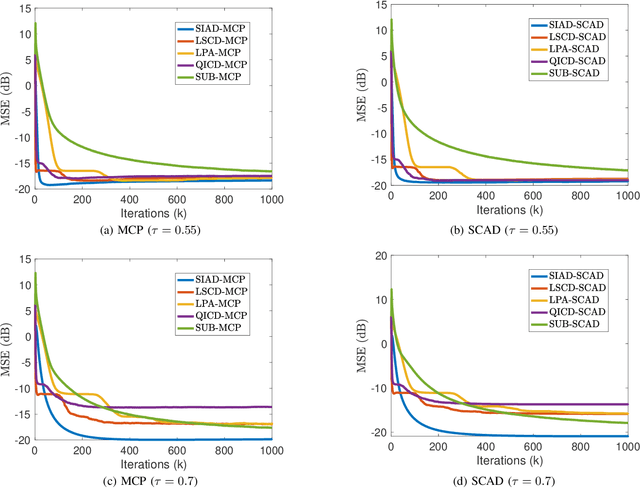
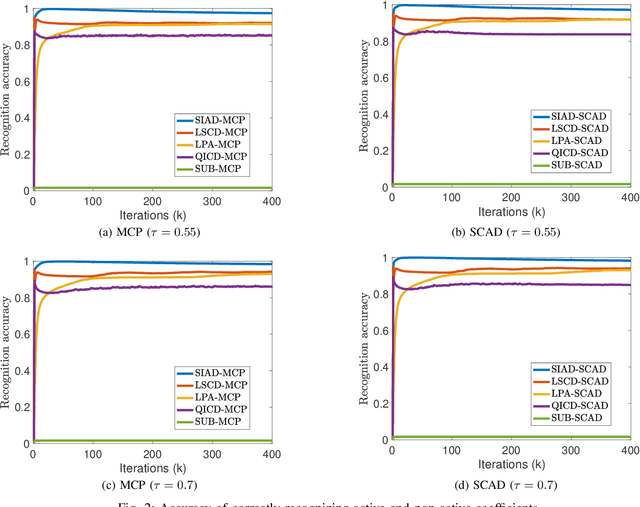
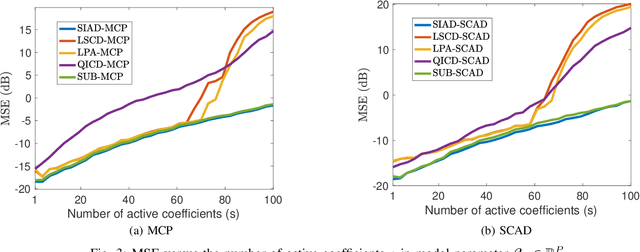
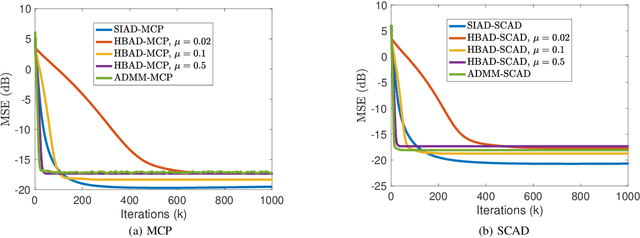
This paper investigates quantile regression in the presence of non-convex and non-smooth sparse penalties, such as the minimax concave penalty (MCP) and smoothly clipped absolute deviation (SCAD). The non-smooth and non-convex nature of these problems often leads to convergence difficulties for many algorithms. While iterative techniques like coordinate descent and local linear approximation can facilitate convergence, the process is often slow. This sluggish pace is primarily due to the need to run these approximation techniques until full convergence at each step, a requirement we term as a \emph{secondary convergence iteration}. To accelerate the convergence speed, we employ the alternating direction method of multipliers (ADMM) and introduce a novel single-loop smoothing ADMM algorithm with an increasing penalty parameter, named SIAD, specifically tailored for sparse-penalized quantile regression. We first delve into the convergence properties of the proposed SIAD algorithm and establish the necessary conditions for convergence. Theoretically, we confirm a convergence rate of $o\big({k^{-\frac{1}{4}}}\big)$ for the sub-gradient bound of augmented Lagrangian. Subsequently, we provide numerical results to showcase the effectiveness of the SIAD algorithm. Our findings highlight that the SIAD method outperforms existing approaches, providing a faster and more stable solution for sparse-penalized quantile regression.

Robust Networked Federated Learning for Localization

This paper addresses the problem of localization, which is inherently non-convex and non-smooth in a federated setting where the data is distributed across a multitude of devices. Due to the decentralized nature of federated environments, distributed learning becomes essential for scalability and adaptability. Moreover, these environments are often plagued by outlier data, which presents substantial challenges to conventional methods, particularly in maintaining estimation accuracy and ensuring algorithm convergence. To mitigate these challenges, we propose a method that adopts an $L_1$-norm robust formulation within a distributed sub-gradient framework, explicitly designed to handle these obstacles. Our approach addresses the problem in its original form, without resorting to iterative simplifications or approximations, resulting in enhanced computational efficiency and improved estimation accuracy. We demonstrate that our method converges to a stationary point, highlighting its effectiveness and reliability. Through numerical simulations, we confirm the superior performance of our approach, notably in outlier-rich environments, which surpasses existing state-of-the-art localization methods.

Moreau Envelope ADMM for Decentralized Weakly Convex Optimization

This paper proposes a proximal variant of the alternating direction method of multipliers (ADMM) for distributed optimization. Although the current versions of ADMM algorithm provide promising numerical results in producing solutions that are close to optimal for many convex and non-convex optimization problems, it remains unclear if they can converge to a stationary point for weakly convex and locally non-smooth functions. Through our analysis using the Moreau envelope function, we demonstrate that MADM can indeed converge to a stationary point under mild conditions. Our analysis also includes computing the bounds on the amount of change in the dual variable update step by relating the gradient of the Moreau envelope function to the proximal function. Furthermore, the results of our numerical experiments indicate that our method is faster and more robust than widely-used approaches.

Distributed Filtering Design with Enhanced Resilience to Coordinated Byzantine Attacks

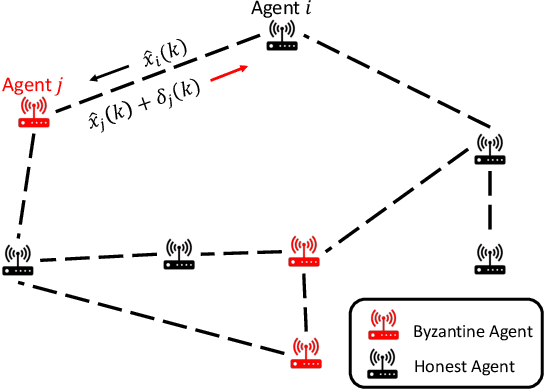
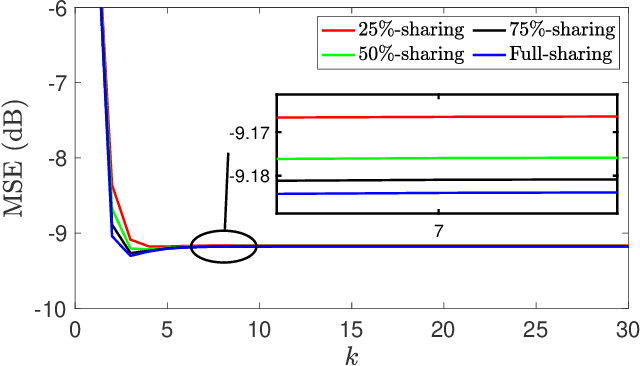
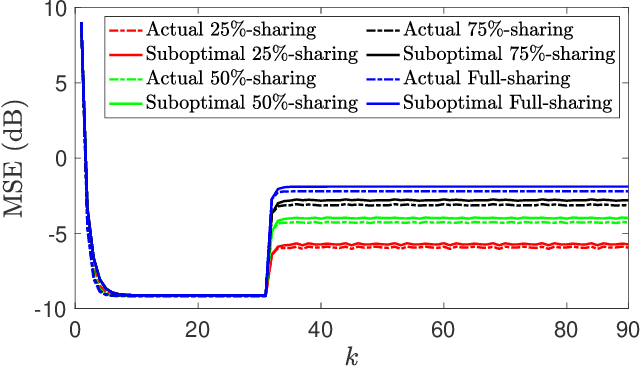
This paper proposes a Byzantine-resilient consensus-based distributed filter (BR-CDF) wherein network agents employ partial sharing of state parameters. We characterize the performance and convergence of the BR-CDF and study the impact of a coordinated data falsification attack. Our analysis shows that sharing merely a fraction of the states improves robustness against coordinated Byzantine attacks. In addition, we model the optimal attack strategy as an optimization problem where Byzantine agents design their attack covariance or the sequence of shared fractions to maximize the network-wide mean squared error (MSE). Numerical results demonstrate the accuracy of the proposed BR-CDF and its robustness against Byzantine attacks. Furthermore, the simulation results show that the influence of the covariance design is more pronounced when agents exchange larger portions of their states with neighbors. In contrast, the performance is more sensitive to the sequence of shared fractions when smaller portions are exchanged.

Hybrid Precoder and Combiner Designs for Decentralized Parameter Estimation in mmWave MIMO Wireless Sensor Networks

Hybrid precoder and combiner designs are conceived for decentralized parameter estimation in millimeter wave (mmWave) multiple-input multiple-output (MIMO) wireless sensor networks (WSNs). More explicitly, efficient pre- and post-processing of the sensor observations and received signal are proposed for the minimum mean square error (MMSE) estimation of a parameter vector. The proposed techniques exploit the limited scattering nature of the mmWave MIMO channel for formulating the hybrid transceiver design framework as a multiple measurement vectors (MMV)-based sparse signal recovery problem. This is then solved using the iterative appealingly low-complexity simultaneous orthogonal matching pursuit (SOMP). Tailor-made designs are presented for WSNs operating under both total and per-sensor power constraints, while considering ideal noiseless as well as realistic noisy sensors. Furthermore, both the Bayesian Cramer-Rao lower bound and the centralized MMSE bound are derived for benchmarking the proposed decentralized estimation schemes. Our simulation results demonstrate the efficiency of the designs advocated and verify the analytical findings.

Zero-Concentrated Private Distributed Learning for Nonsmooth Objective Functions

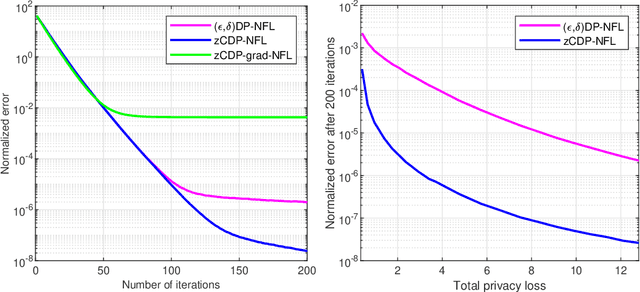
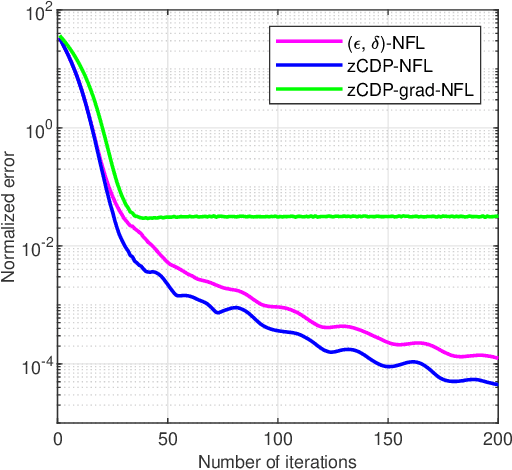
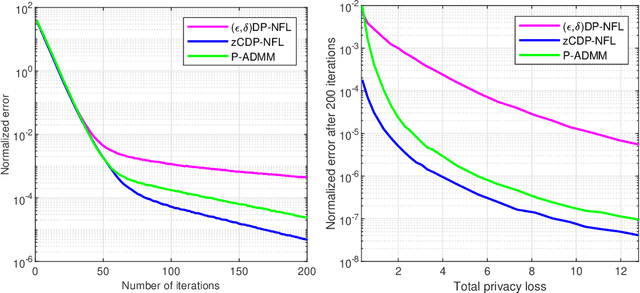
This paper develops a fully distributed differentially-private learning algorithm to solve nonsmooth optimization problems. We distribute the Alternating Direction Method of Multipliers (ADMM) to comply with the distributed setting and employ an approximation of the augmented Lagrangian to handle nonsmooth objective functions. Furthermore, we ensure zero-concentrated differential privacy (zCDP) by perturbing the outcome of the computation at each agent with a variance-decreasing Gaussian noise. This privacy-preserving method allows for better accuracy than the conventional $(\epsilon, \delta)$-DP and stronger guarantees than the more recent R\'enyi-DP. The developed fully distributed algorithm has a competitive privacy accuracy trade-off and handles nonsmooth and non-necessarily strongly convex problems. We provide complete theoretical proof for the privacy guarantees and the convergence of the algorithm to the exact solution. We also prove under additional assumptions that the algorithm converges in linear time. Finally, we observe in simulations that the developed algorithm outperforms all of the existing methods.

Robust Hybrid Transceiver Designs for Linear Decentralized Estimation in mmWave MIMO IoT Networks in the Face of Imperfect CSI

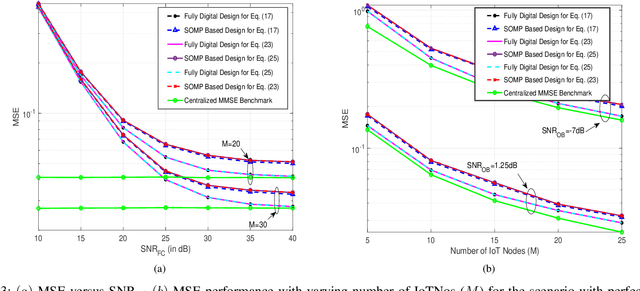
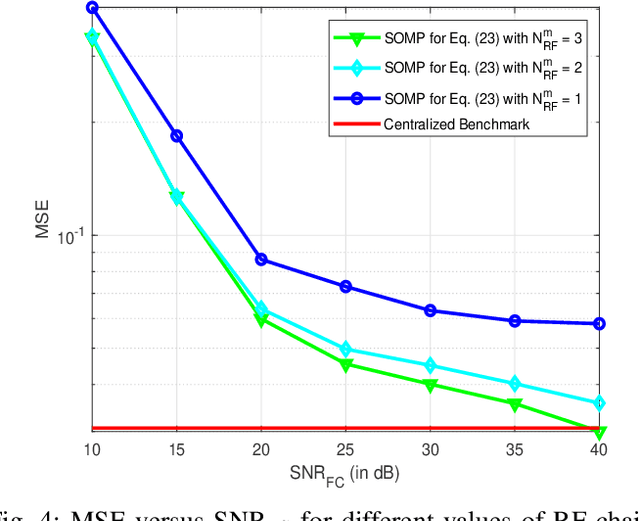
Hybrid transceivers are designed for linear decentralized estimation (LDE) in a mmWave multiple-input multiple-output (MIMO) IoT network (IoTNe). For a noiseless fusion center (FC), it is demonstrated that the MSE performance is determined by the number of RF chains used at each IoT node (IoTNo). Next, the minimum-MSE RF transmit precoders (TPCs) and receive combiner (RC) matrices are designed for this setup using the dominant array response vectors, and subsequently, a closed-form expression is obtained for the baseband (BB) TPC at each IoTNo using Cauchy's interlacing theorem. For a realistic noisy FC, it is shown that the resultant mean squared error (MSE) minimization problem is non-convex. To address this challenge, a block-coordinate descent-based iterative scheme is proposed to obtain the fully digital TPC and RC matrices followed by the simultaneous orthogonal matching pursuit (SOMP) technique for decomposing the fully-digital transceiver into its corresponding RF and BB components. A theoretical proof of the convergence is also presented for the proposed iterative design procedure. Furthermore, robust hybrid transceiver designs are also derived for a practical scenario in the face of channel state information (CSI) uncertainty. The centralized MMSE lower bound has also been derived that benchmarks the performance of the proposed LDE schemes. Finally, our numerical results characterize the performance of the proposed transceivers as well as corroborate our various analytical propositions.

Robust Linear Hybrid Beamforming Designs Relying on Imperfect CSI in mmWave MIMO IoT Networks

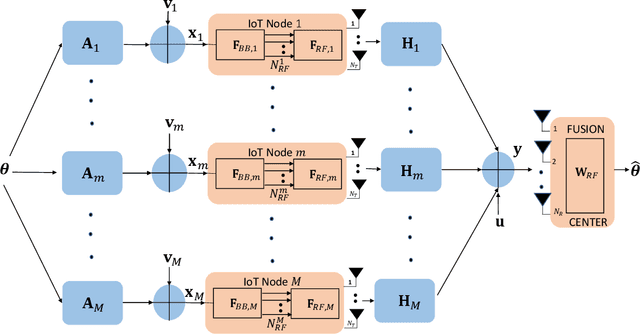
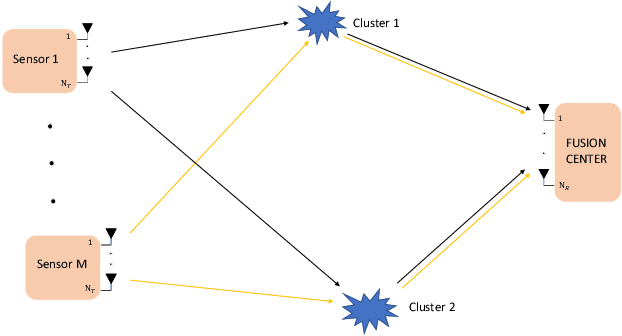
Linear hybrid beamformer designs are conceived for the decentralized estimation of a vector parameter in a millimeter wave (mmWave) multiple-input multiple-output (MIMO) Internet of Things network (IoTNe). The proposed designs incorporate both total IoTNe and individual IoTNo power constraints, while also eliminating the need for a baseband receiver combiner at the fusion center (FC). To circumvent the non-convexity of the hybrid beamformer design problem, the proposed approach initially determines the minimum mean square error (MMSE) digital transmit precoder (TPC) weights followed by a simultaneous orthogonal matching pursuit (SOMP)-based framework for obtaining the analog RF and digital baseband TPCs. Robust hybrid beamformers are also derived for the realistic imperfect channel state information (CSI) scenario, utilizing both the stochastic and norm-ball CSI uncertainty frameworks. The centralized MMSE bound derived in this work serves as a lower bound for the estimation performance of the proposed hybrid TPC designs. Finally, our simulation results quantify the benefits of the various designs developed.

Cooperative Hybrid Transmit Beamforming in Cell-free mmWave MIMO Networks

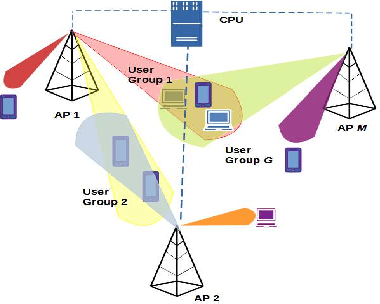
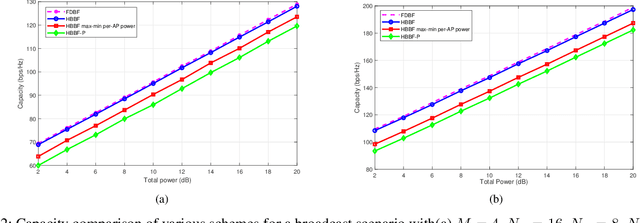
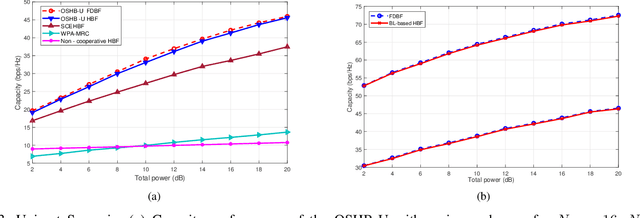
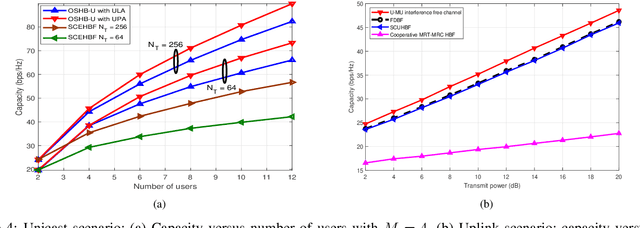
Hybrid precoders and combiners are designed for cooperative cell-free multi-user millimeter wave (mmWave) multiple-input multiple-output (MIMO) cellular networks for low complexity interference mitigation. Initially, we derive an optimal hybrid transmit beamformer (HTBF) for a broadcast scenario considering both total and per access point (AP) power constraints. Next, an optimal successive hybrid beamformer technique is proposed for unicast and multicast scenarios which relies on the optimal minimum variance distortionless response (MVDR). We demonstrate that it mitigates both the interuser and intergroup interference, while successively ensuring orthogonality to the previously scheduled users/user groups. Furthermore, it is shown theoretically that the proposed schemes are capable of supporting a large number of users. Subsequently, a Bayesian learning (BL) based method is conceived for jointly designing the RF and baseband precoders/combiners for the various scenarios considered. Furthermore, we also conceive the uplink counterpart of our HTBF scheme, which is based on maximizing the signal-tointerference-plus noise ratio (SINR) of each individual user. Finally, the efficacy of the proposed schemes is characterized by our extensive simulation results in terms of cancelling the interuser/intergroup interference, which improves the spectral efficiency.