Monotone Lipschitz-Gradient Denoiser: Explainability of Operator Regularization Approaches and Convergence to Optimal Point

This paper addresses explainability of the operator-regularization approach under the use of monotone Lipschitz-gradient (MoL-Grad) denoiser -- an operator that can be expressed as the Lipschitz continuous gradient of a differentiable convex function. We prove that an operator is a MoL-Grad denoiser if and only if it is the ``single-valued'' proximity operator of a weakly convex function. An extension of Moreau's decomposition is also shown with respect to a weakly convex function and the conjugate of its convexified function. Under these arguments, two specific algorithms, the forward-backward splitting algorithm and the primal-dual splitting algorithm, are considered, both employing MoL-Grad denoisers. These algorithms generate a sequence of vectors converging weakly, under conditions, to a minimizer of a certain cost function which involves an ``implicit regularizer'' induced by the denoiser. The theoretical findings are supported by simulations.

Linearly-involved Moreau-Enhanced-over-Subspace Model: Debiased Sparse Modeling and Stable Outlier-Robust Regression

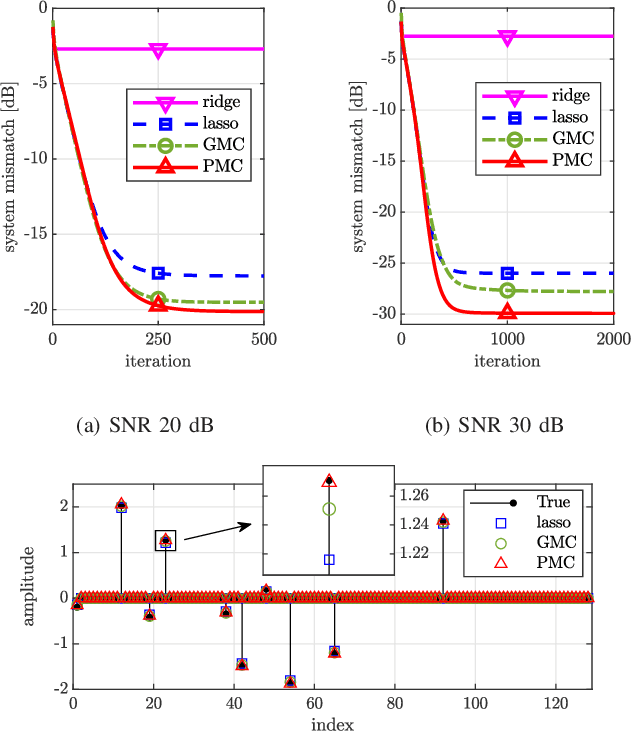
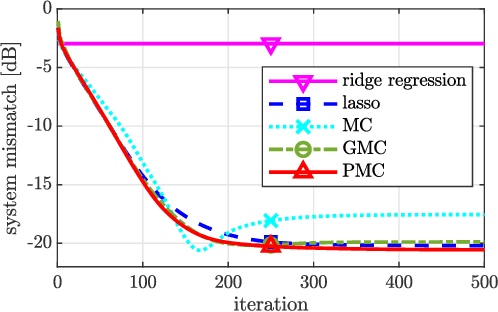
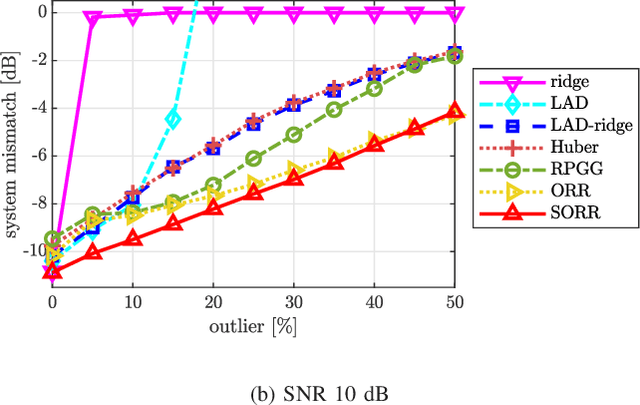
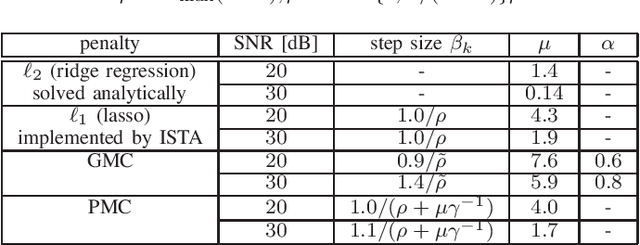
We present an efficient mathematical framework based on the linearly-involved Moreau-enhanced-over-subspace (LiMES) model. Two concrete applications are considered: sparse modeling and robust regression. The popular minimax concave (MC) penalty for sparse modeling subtracts, from the $\ell_1$ norm, its Moreau envelope, inducing nearly unbiased estimates and thus yielding remarkable performance enhancements. To extend it to underdetermined linear systems, we propose the projective minimax concave penalty using the projection onto the input subspace, where the Moreau-enhancement effect is restricted to the subspace for preserving the overall convexity. We also present a novel concept of stable outlier-robust regression which distinguishes noise and outlier explicitly. The LiMES model encompasses those two specific examples as well as two other applications: stable principal component pursuit and robust classification. The LiMES function involved in the model is an ``additively nonseparable'' weakly convex function but is defined with the Moreau envelope returning the minimum of a ``separable'' convex function. This mixed nature of separability and nonseparability allows an application of the LiMES model to the underdetermined case with an efficient algorithmic implementation. Two linear/affine operators play key roles in the model: one corresponds to the projection mentioned above and the other takes care of robust regression/classification. A necessary and sufficient condition for convexity of the smooth part of the objective function is studied. Numerical examples show the efficacy of LiMES in applications to sparse modeling and robust regression.

Learning Sparse Graph with Minimax Concave Penalty under Gaussian Markov Random Fields

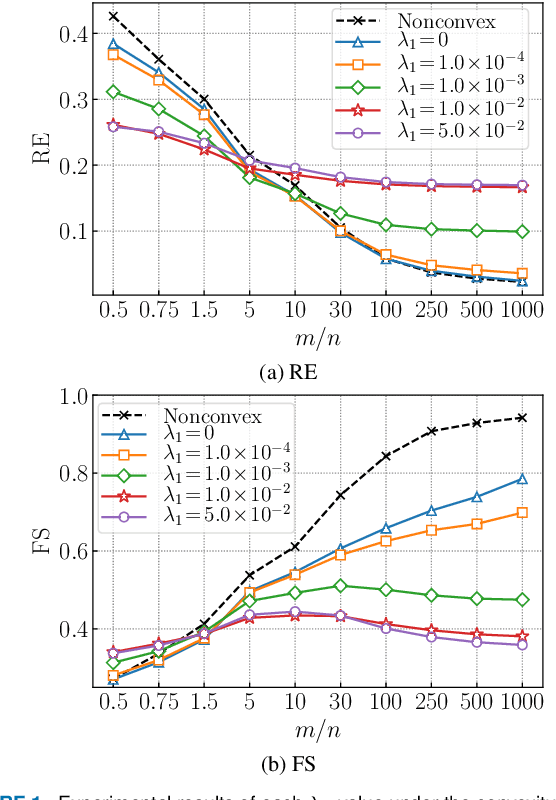
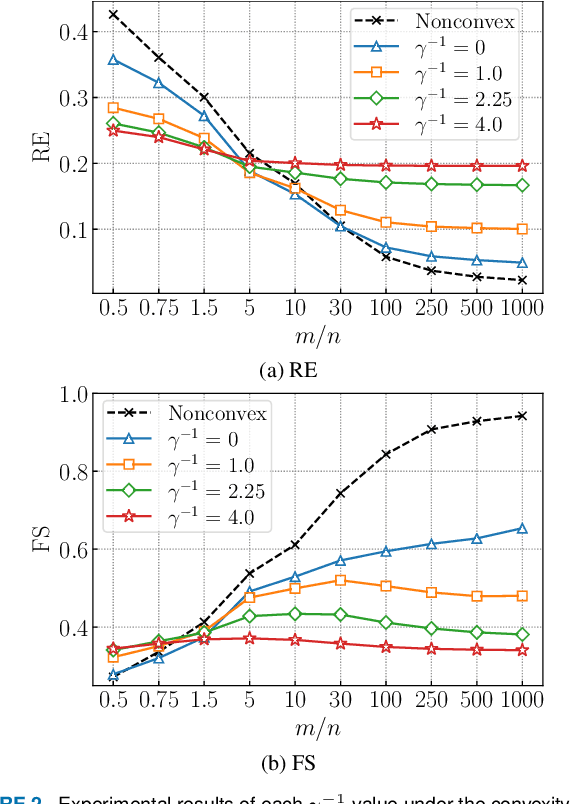
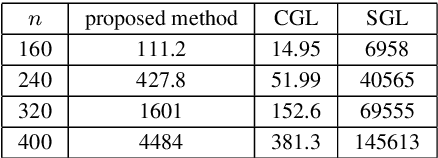
This paper presents a convex-analytic framework to learn sparse graphs from data. While our problem formulation is inspired by an extension of the graphical lasso using the so-called combinatorial graph Laplacian framework, a key difference is the use of a nonconvex alternative to the $\ell_1$ norm to attain graphs with better interpretability. Specifically, we use the weakly-convex minimax concave penalty (the difference between the $\ell_1$ norm and the Huber function) which is known to yield sparse solutions with lower estimation bias than $\ell_1$ for regression problems. In our framework, the graph Laplacian is replaced in the optimization by a linear transform of the vector corresponding to its upper triangular part. Via a reformulation relying on Moreau's decomposition, we show that overall convexity is guaranteed by introducing a quadratic function to our cost function. The problem can be solved efficiently by the primal-dual splitting method, of which the admissible conditions for provable convergence are presented. Numerical examples show that the proposed method significantly outperforms the existing graph learning methods with reasonable CPU time.

Continuous-time Value Function Approximation in Reproducing Kernel Hilbert Spaces

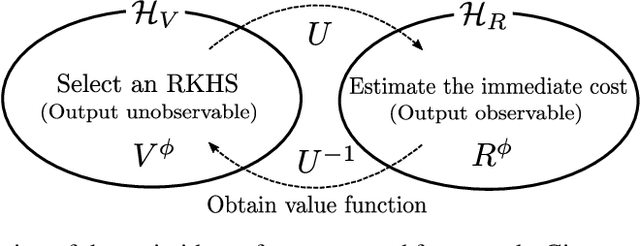
Motivated by the success of reinforcement learning (RL) for discrete-time tasks such as AlphaGo and Atari games, there has been a recent surge of interest in using RL for continuous-time control of physical systems (cf. many challenging tasks in OpenAI Gym and DeepMind Control Suite). Since discretization of time is susceptible to error, it is methodologically more desirable to handle the system dynamics directly in continuous time. However, very few techniques exist for continuous-time RL and they lack flexibility in value function approximation. In this paper, we propose a novel framework for model-based continuous-time value function approximation in reproducing kernel Hilbert spaces. The resulting framework is so flexible that it can accommodate any kind of kernel-based approach, such as Gaussian processes and kernel adaptive filters, and it allows us to handle uncertainties and nonstationarity without prior knowledge about the environment or what basis functions to employ. We demonstrate the validity of the presented framework through experiments.

Detection for 5G-NOMA: An Online Adaptive Machine Learning Approach

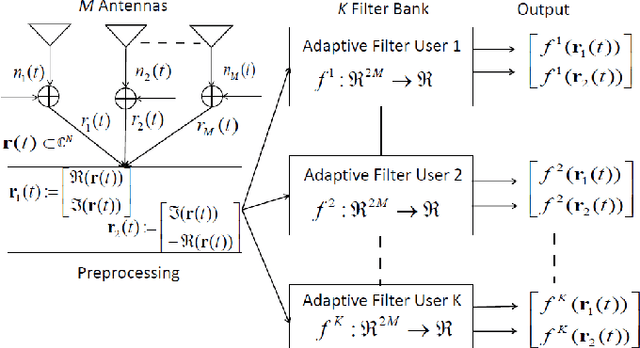
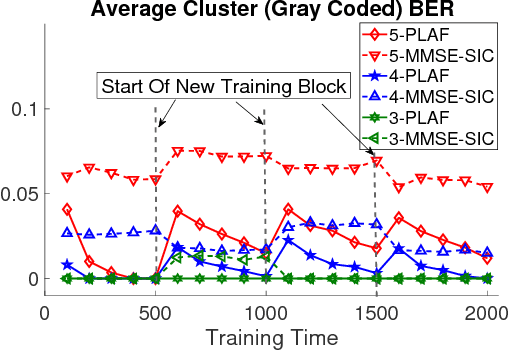
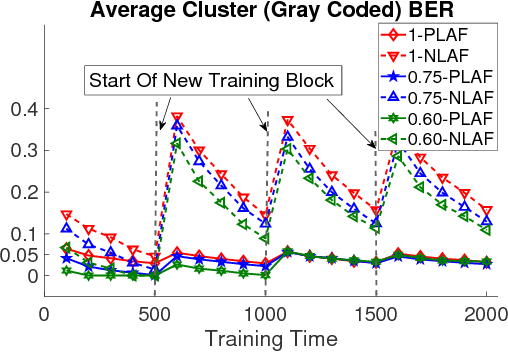
Non-orthogonal multiple access (NOMA) has emerged as a promising radio access technique for enabling the performance enhancements promised by the fifth-generation (5G) networks in terms of connectivity, low latency, and high spectrum efficiency. In the NOMA uplink, successive interference cancellation (SIC) based detection with device clustering has been suggested. In the case of multiple receive antennas, SIC can be combined with the minimum mean-squared error (MMSE) beamforming. However, there exists a tradeoff between the NOMA cluster size and the incurred SIC error. Larger clusters lead to larger errors but they are desirable from the spectrum efficiency and connectivity point of view. We propose a novel online learning based detection for the NOMA uplink. In particular, we design an online adaptive filter in the sum space of linear and Gaussian reproducing kernel Hilbert spaces (RKHSs). Such a sum space design is robust against variations of a dynamic wireless network that can deteriorate the performance of a purely nonlinear adaptive filter. We demonstrate by simulations that the proposed method outperforms the MMSE-SIC based detection for large cluster sizes.

Kernel-Based Adaptive Online Reconstruction of Coverage Maps With Side Information

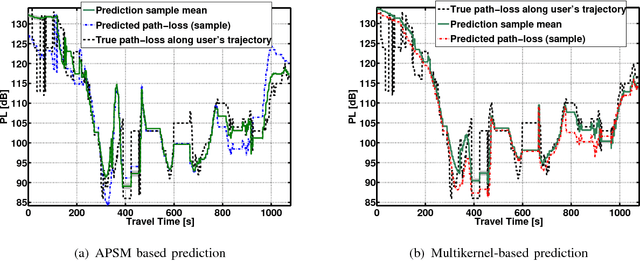
In this paper, we address the problem of reconstructing coverage maps from path-loss measurements in cellular networks. We propose and evaluate two kernel-based adaptive online algorithms as an alternative to typical offline methods. The proposed algorithms are application-tailored extensions of powerful iterative methods such as the adaptive projected subgradient method and a state-of-the-art adaptive multikernel method. Assuming that the moving trajectories of users are available, it is shown how side information can be incorporated in the algorithms to improve their convergence performance and the quality of the estimation. The complexity is significantly reduced by imposing sparsity-awareness in the sense that the algorithms exploit the compressibility of the measurement data to reduce the amount of data which is saved and processed. Finally, we present extensive simulations based on realistic data to show that our algorithms provide fast, robust estimates of coverage maps in real-world scenarios. Envisioned applications include path-loss prediction along trajectories of mobile users as a building block for anticipatory buffering or traffic offloading.

Adaptive Learning in Cartesian Product of Reproducing Kernel Hilbert Spaces

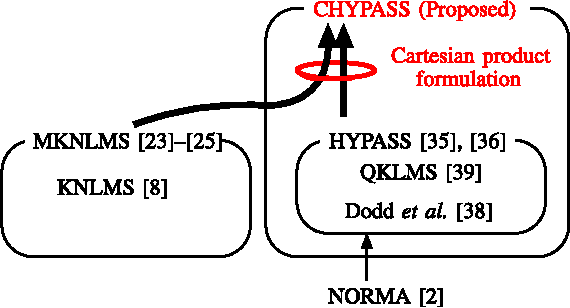
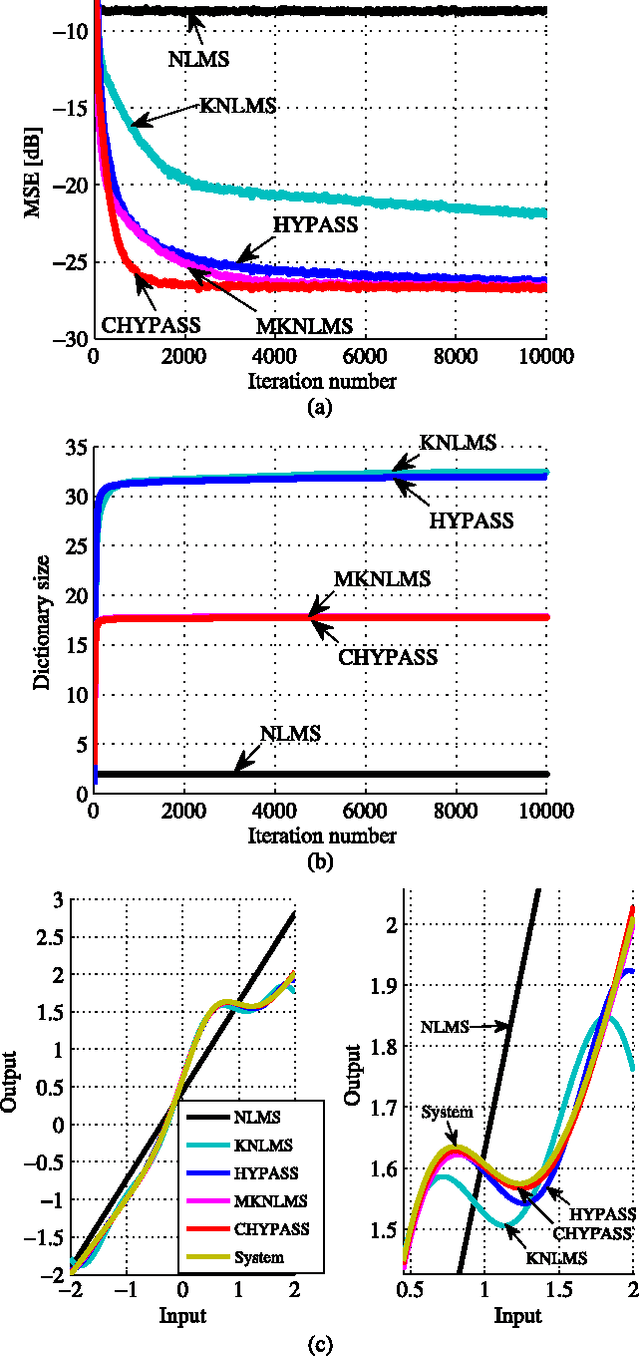
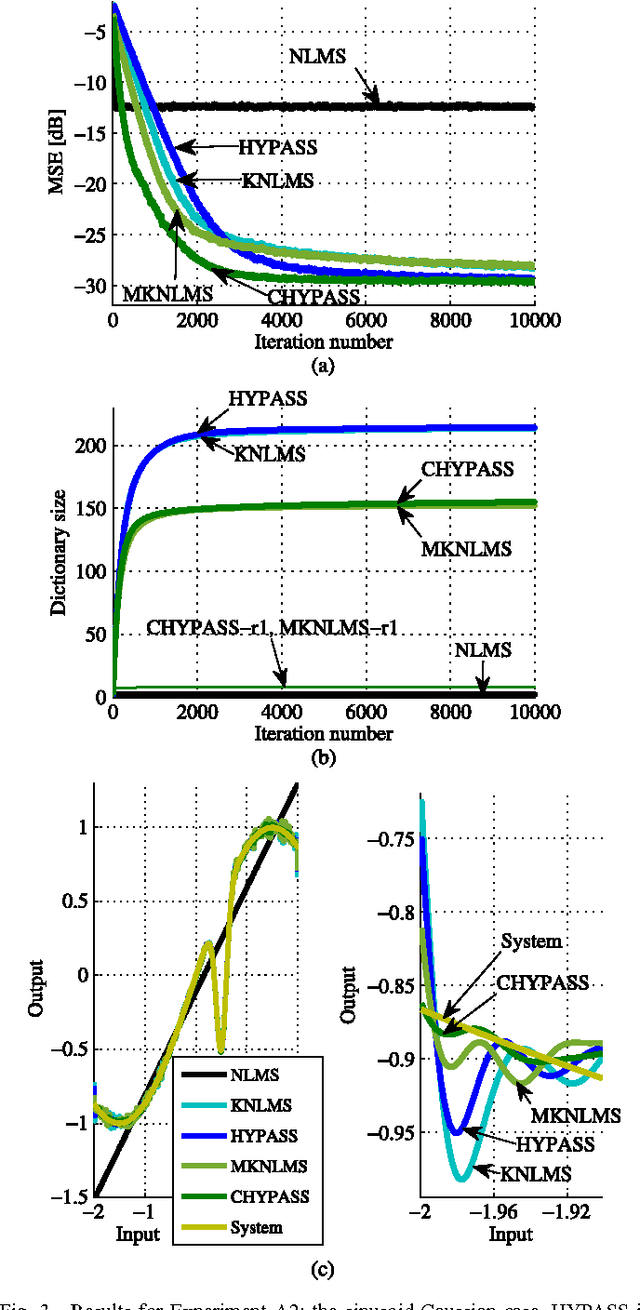
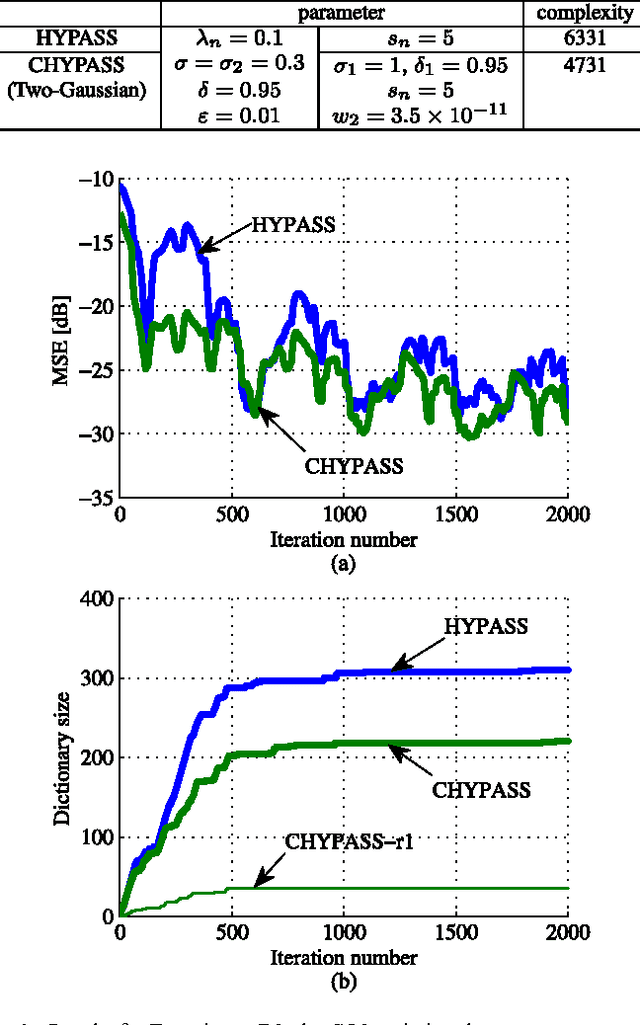
We propose a novel adaptive learning algorithm based on iterative orthogonal projections in the Cartesian product of multiple reproducing kernel Hilbert spaces (RKHSs). The task is estimating/tracking nonlinear functions which are supposed to contain multiple components such as (i) linear and nonlinear components, (ii) high- and low- frequency components etc. In this case, the use of multiple RKHSs permits a compact representation of multicomponent functions. The proposed algorithm is where two different methods of the author meet: multikernel adaptive filtering and the algorithm of hyperplane projection along affine subspace (HYPASS). In a certain particular case, the sum space of the RKHSs is isomorphic to the product space and hence the proposed algorithm can also be regarded as an iterative projection method in the sum space. The efficacy of the proposed algorithm is shown by numerical examples.

A stochastic behavior analysis of stochastic restricted-gradient descent algorithm in reproducing kernel Hilbert spaces

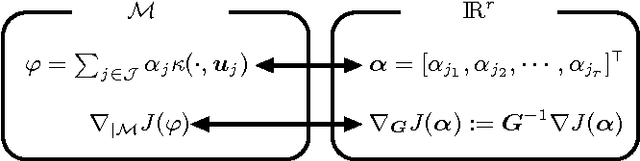
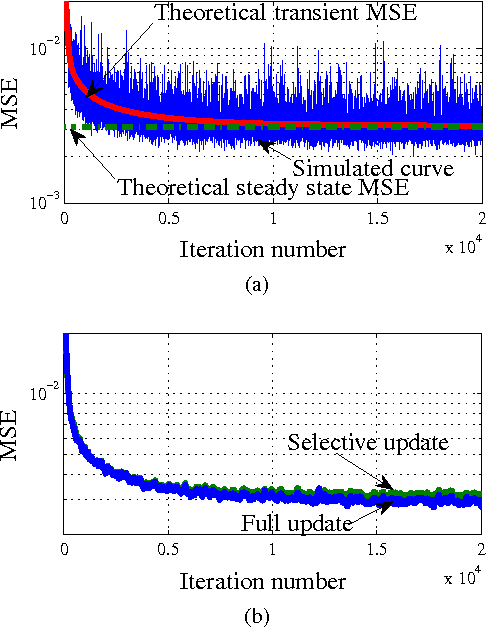
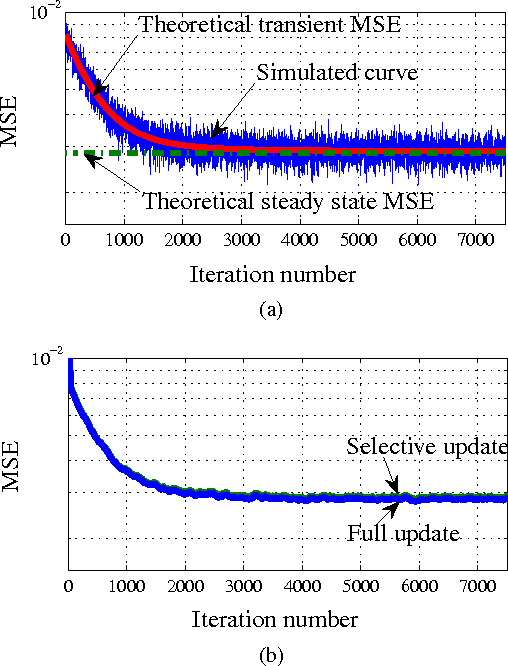
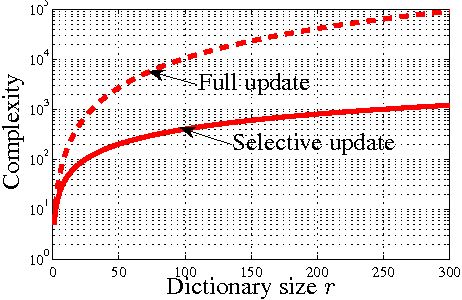
This paper presents a stochastic behavior analysis of a kernel-based stochastic restricted-gradient descent method. The restricted gradient gives a steepest ascent direction within the so-called dictionary subspace. The analysis provides the transient and steady state performance in the mean squared error criterion. It also includes stability conditions in the mean and mean-square sense. The present study is based on the analysis of the kernel normalized least mean square (KNLMS) algorithm initially proposed by Chen et al. Simulation results validate the analysis.