Signatures Meet Dynamic Programming: Generalizing Bellman Equations for Trajectory Following

Path signatures have been proposed as a powerful representation of paths that efficiently captures the path's analytic and geometric characteristics, having useful algebraic properties including fast concatenation of paths through tensor products. Signatures have recently been widely adopted in machine learning problems for time series analysis. In this work we establish connections between value functions typically used in optimal control and intriguing properties of path signatures. These connections motivate our novel control framework with signature transforms that efficiently generalizes the Bellman equation to the space of trajectories. We analyze the properties and advantages of the framework, termed signature control. In particular, we demonstrate that (i) it can naturally deal with varying/adaptive time steps; (ii) it propagates higher-level information more efficiently than value function updates; (iii) it is robust to dynamical system misspecification over long rollouts. As a specific case of our framework, we devise a model predictive control method for path tracking. This method generalizes integral control, being suitable for problems with unknown disturbances. The proposed algorithms are tested in simulation, with differentiable physics models including typical control and robotics tasks such as point-mass, curve following for an ant model, and a robotic manipulator.

Dynamic Structure Estimation from Bandit Feedback

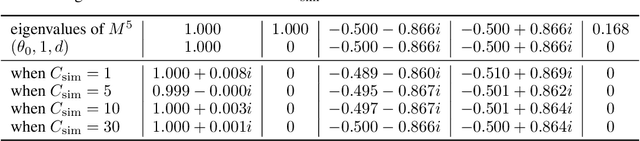
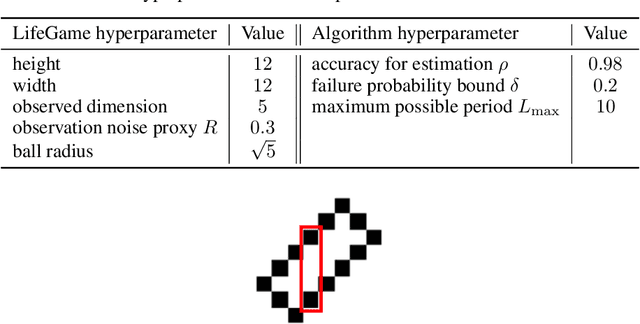
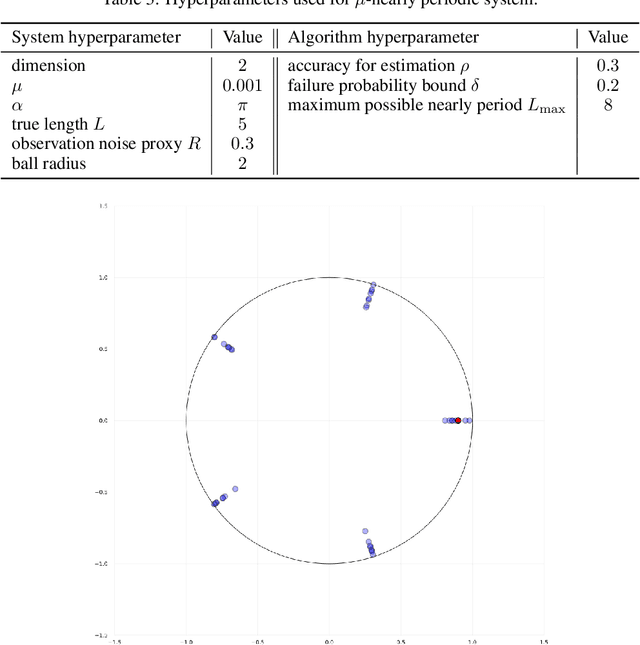
This work present novel method for structure estimation of an underlying dynamical system. We tackle problems of estimating dynamic structure from bandit feedback contaminated by sub-Gaussian noise. In particular, we focus on periodically behaved discrete dynamical system in the Euclidean space, and carefully identify certain obtainable subset of full information of the periodic structure. We then derive a sample complexity bound for periodic structure estimation. Technically, asymptotic results for exponential sums are adopted to effectively average out the noise effects while preventing the information to be estimated from vanishing. For linear systems, the use of the Weyl sum further allows us to extract eigenstructures. Our theoretical claims are experimentally validated on simulations of toy examples, including Cellular Automata.

Koopman Spectrum Nonlinear Regulator and Provably Efficient Online Learning

Most modern reinforcement learning algorithms optimize a cumulative single-step cost along a trajectory. The optimized motions are often 'unnatural', representing, for example, behaviors with sudden accelerations that waste energy and lack predictability. In this work, we present a novel paradigm of controlling nonlinear systems via the minimization of the Koopman spectrum cost: a cost over the Koopman operator of the controlled dynamics. This induces a broader class of dynamical behaviors that evolve over stable manifolds such as nonlinear oscillators, closed loops, and smooth movements. We demonstrate that some dynamics realizations that are not possible with a cumulative cost are feasible in this paradigm. Moreover, we present a provably efficient online learning algorithm for our problem that enjoys a sub-linear regret bound under some structural assumptions.

Information Theoretic Regret Bounds for Online Nonlinear Control

This work studies the problem of sequential control in an unknown, nonlinear dynamical system, where we model the underlying system dynamics as an unknown function in a known Reproducing Kernel Hilbert Space. This framework yields a general setting that permits discrete and continuous control inputs as well as non-smooth, non-differentiable dynamics. Our main result, the Lower Confidence-based Continuous Control ($LC^3$) algorithm, enjoys a near-optimal $O(\sqrt{T})$ regret bound against the optimal controller in episodic settings, where $T$ is the number of episodes. The bound has no explicit dependence on dimension of the system dynamics, which could be infinite, but instead only depends on information theoretic quantities. We empirically show its application to a number of nonlinear control tasks and demonstrate the benefit of exploration for learning model dynamics.

Continuous-time Value Function Approximation in Reproducing Kernel Hilbert Spaces

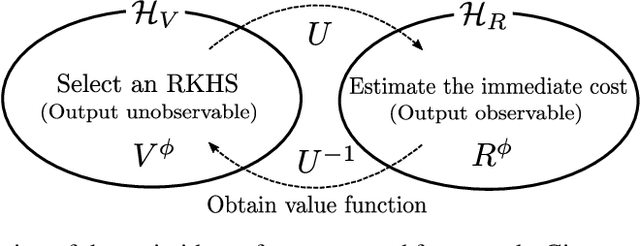
Motivated by the success of reinforcement learning (RL) for discrete-time tasks such as AlphaGo and Atari games, there has been a recent surge of interest in using RL for continuous-time control of physical systems (cf. many challenging tasks in OpenAI Gym and DeepMind Control Suite). Since discretization of time is susceptible to error, it is methodologically more desirable to handle the system dynamics directly in continuous time. However, very few techniques exist for continuous-time RL and they lack flexibility in value function approximation. In this paper, we propose a novel framework for model-based continuous-time value function approximation in reproducing kernel Hilbert spaces. The resulting framework is so flexible that it can accommodate any kind of kernel-based approach, such as Gaussian processes and kernel adaptive filters, and it allows us to handle uncertainties and nonstationarity without prior knowledge about the environment or what basis functions to employ. We demonstrate the validity of the presented framework through experiments.

Barrier-Certified Adaptive Reinforcement Learning with Applications to Brushbot Navigation

This paper presents a safe learning framework that employs an adaptive model learning method together with barrier certificates for systems with possibly nonstationary agent dynamics. To extract the dynamic structure of the model, we use a sparse optimization technique, and the resulting model will be used in combination with control barrier certificates which constrain policies (feedback controllers) in order to maintain safety, which refers to avoiding certain regions of the state space. Under certain conditions, recovery of safety in the sense of Lyapunov stability after violations of safety due to the nonstationarity is guaranteed. In addition, we reformulate action-value function approximation to make any kernel-based nonlinear function estimation method applicable to our adaptive learning framework. Lastly, solutions to the barrier-certified policy optimization are guaranteed to be globally optimal, ensuring greedy policy updates under mild conditions. The resulting framework is validated via simulations of a quadrotor, which has been used in the safe learnings literature under {\em stationarity} assumption, and then tested on a real robot called {\em brushbot}, whose dynamics is unknown, highly complex, and most probably nonstationary.