Locally Differentially Private Online Federated Learning With Correlated Noise

We introduce a locally differentially private (LDP) algorithm for online federated learning that employs temporally correlated noise to improve utility while preserving privacy. To address challenges posed by the correlated noise and local updates with streaming non-IID data, we develop a perturbed iterate analysis that controls the impact of the noise on the utility. Moreover, we demonstrate how the drift errors from local updates can be effectively managed for several classes of nonconvex loss functions. Subject to an $(\epsilon,\delta)$-LDP budget, we establish a dynamic regret bound that quantifies the impact of key parameters and the intensity of changes in the dynamic environment on the learning performance. Numerical experiments confirm the efficacy of the proposed algorithm.

From promise to practice: realizing high-performance decentralized training

Decentralized training of deep neural networks has attracted significant attention for its theoretically superior scalability over synchronous data-parallel methods like All-Reduce. However, realizing this potential in multi-node training is challenging due to the complex design space that involves communication topologies, computation patterns, and optimization algorithms. This paper identifies three key factors that can lead to speedups over All-Reduce training and constructs a runtime model to determine when, how, and to what degree decentralization can yield shorter per-iteration runtimes. Furthermore, to support the decentralized training of transformer-based models, we study a decentralized Adam algorithm that allows for overlapping communications and computations, prove its convergence, and propose an accumulation technique to mitigate the high variance caused by small local batch sizes. We deploy the proposed approach in clusters with up to 64 GPUs and demonstrate its practicality and advantages in both runtime and generalization performance under a fixed iteration budget.

Temporal Predictive Coding for Gradient Compression in Distributed Learning

This paper proposes a prediction-based gradient compression method for distributed learning with event-triggered communication. Our goal is to reduce the amount of information transmitted from the distributed agents to the parameter server by exploiting temporal correlation in the local gradients. We use a linear predictor that \textit{combines past gradients to form a prediction of the current gradient}, with coefficients that are optimized by solving a least-square problem. In each iteration, every agent transmits the predictor coefficients to the server such that the predicted local gradient can be computed. The difference between the true local gradient and the predicted one, termed the \textit{prediction residual, is only transmitted when its norm is above some threshold.} When this additional communication step is omitted, the server uses the prediction as the estimated gradient. This proposed design shows notable performance gains compared to existing methods in the literature, achieving convergence with reduced communication costs.

Nonconvex Federated Learning on Compact Smooth Submanifolds With Heterogeneous Data

Many machine learning tasks, such as principal component analysis and low-rank matrix completion, give rise to manifold optimization problems. Although there is a large body of work studying the design and analysis of algorithms for manifold optimization in the centralized setting, there are currently very few works addressing the federated setting. In this paper, we consider nonconvex federated learning over a compact smooth submanifold in the setting of heterogeneous client data. We propose an algorithm that leverages stochastic Riemannian gradients and a manifold projection operator to improve computational efficiency, uses local updates to improve communication efficiency, and avoids client drift. Theoretically, we show that our proposed algorithm converges sub-linearly to a neighborhood of a first-order optimal solution by using a novel analysis that jointly exploits the manifold structure and properties of the loss functions. Numerical experiments demonstrate that our algorithm has significantly smaller computational and communication overhead than existing methods.

Differentially Private Online Federated Learning with Correlated Noise

We propose a novel differentially private algorithm for online federated learning that employs temporally correlated noise to improve the utility while ensuring the privacy of the continuously released models. To address challenges stemming from DP noise and local updates with streaming noniid data, we develop a perturbed iterate analysis to control the impact of the DP noise on the utility. Moreover, we demonstrate how the drift errors from local updates can be effectively managed under a quasi-strong convexity condition. Subject to an $(\epsilon, \delta)$-DP budget, we establish a dynamic regret bound over the entire time horizon that quantifies the impact of key parameters and the intensity of changes in dynamic environments. Numerical experiments validate the efficacy of the proposed algorithm.

Asynchronous Distributed Optimization with Delay-free Parameters

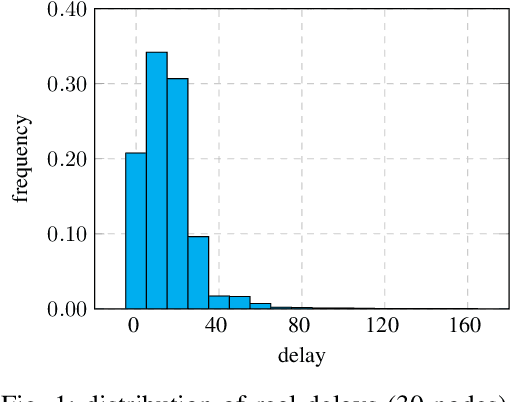
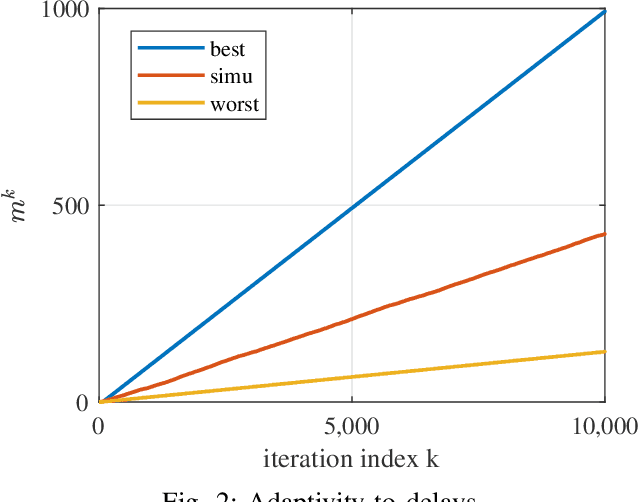
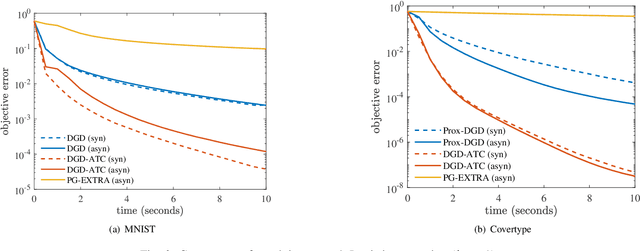
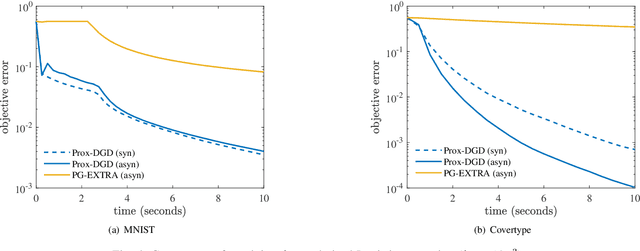
Existing asynchronous distributed optimization algorithms often use diminishing step-sizes that cause slow practical convergence, or use fixed step-sizes that depend on and decrease with an upper bound of the delays. Not only are such delay bounds hard to obtain in advance, but they also tend to be large and rarely attained, resulting in unnecessarily slow convergence. This paper develops asynchronous versions of two distributed algorithms, Prox-DGD and DGD-ATC, for solving consensus optimization problems over undirected networks. In contrast to alternatives, our algorithms can converge to the fixed point set of their synchronous counterparts using step-sizes that are independent of the delays. We establish convergence guarantees for strongly and weakly convex problems under both partial and total asynchrony. We also show that the convergence speed of the two asynchronous methods adapts to the actual level of asynchrony rather than being constrained by the worst-case. Numerical experiments demonstrate a strong practical performance of our asynchronous algorithms.

Composite federated learning with heterogeneous data

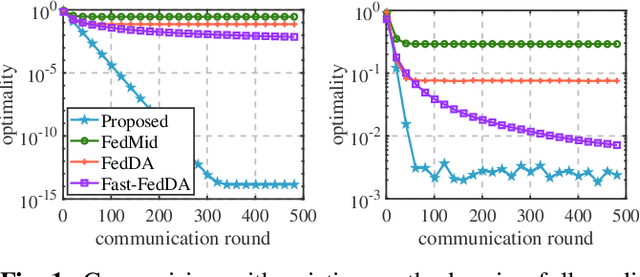
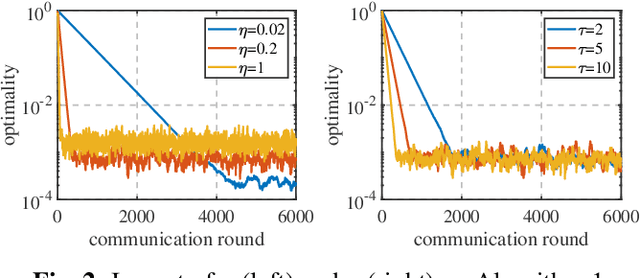
We propose a novel algorithm for solving the composite Federated Learning (FL) problem. This algorithm manages non-smooth regularization by strategically decoupling the proximal operator and communication, and addresses client drift without any assumptions about data similarity. Moreover, each worker uses local updates to reduce the communication frequency with the server and transmits only a $d$-dimensional vector per communication round. We prove that our algorithm converges linearly to a neighborhood of the optimal solution and demonstrate the superiority of our algorithm over state-of-the-art methods in numerical experiments.

Dynamic Privacy Allocation for Locally Differentially Private Federated Learning with Composite Objectives

This paper proposes a locally differentially private federated learning algorithm for strongly convex but possibly nonsmooth problems that protects the gradients of each worker against an honest but curious server. The proposed algorithm adds artificial noise to the shared information to ensure privacy and dynamically allocates the time-varying noise variance to minimize an upper bound of the optimization error subject to a predefined privacy budget constraint. This allows for an arbitrarily large but finite number of iterations to achieve both privacy protection and utility up to a neighborhood of the optimal solution, removing the need for tuning the number of iterations. Numerical results show the superiority of the proposed algorithm over state-of-the-art methods.

Bringing regularized optimal transport to lightspeed: a splitting method adapted for GPUs

We present an efficient algorithm for regularized optimal transport. In contrast to previous methods, we use the Douglas-Rachford splitting technique to develop an efficient solver that can handle a broad class of regularizers. The algorithm has strong global convergence guarantees, low per-iteration cost, and can exploit GPU parallelization, making it considerably faster than the state-of-the-art for many problems. We illustrate its competitiveness in several applications, including domain adaptation and learning of generative models.

Over-the-Air Computation for Distributed Systems: Something Old and Something New

Facing the upcoming era of Internet-of-Things and connected intelligence, efficient information processing, computation and communication design becomes a key challenge in large-scale intelligent systems. Recently, Over-the-Air (OtA) computation has been proposed for data aggregation and distributed function computation over a large set of network nodes. Theoretical foundations for this concept exist for a long time, but it was mainly investigated within the context of wireless sensor networks. There are still many open questions when applying OtA computation in different types of distributed systems where modern wireless communication technology is applied. In this article, we provide a comprehensive overview of the OtA computation principle and its applications in distributed learning, control, and inference systems, for both server-coordinated and fully decentralized architectures. Particularly, we highlight the importance of the statistical heterogeneity of data and wireless channels, the temporal evolution of model updates, and the choice of performance metrics, for the communication design in OtA federated learning (FL) systems. Several key challenges in privacy, security and robustness aspects of OtA FL are also identified for further investigation.