Locally Differentially Private Online Federated Learning With Correlated Noise

We introduce a locally differentially private (LDP) algorithm for online federated learning that employs temporally correlated noise to improve utility while preserving privacy. To address challenges posed by the correlated noise and local updates with streaming non-IID data, we develop a perturbed iterate analysis that controls the impact of the noise on the utility. Moreover, we demonstrate how the drift errors from local updates can be effectively managed for several classes of nonconvex loss functions. Subject to an $(\epsilon,\delta)$-LDP budget, we establish a dynamic regret bound that quantifies the impact of key parameters and the intensity of changes in the dynamic environment on the learning performance. Numerical experiments confirm the efficacy of the proposed algorithm.

From promise to practice: realizing high-performance decentralized training

Decentralized training of deep neural networks has attracted significant attention for its theoretically superior scalability over synchronous data-parallel methods like All-Reduce. However, realizing this potential in multi-node training is challenging due to the complex design space that involves communication topologies, computation patterns, and optimization algorithms. This paper identifies three key factors that can lead to speedups over All-Reduce training and constructs a runtime model to determine when, how, and to what degree decentralization can yield shorter per-iteration runtimes. Furthermore, to support the decentralized training of transformer-based models, we study a decentralized Adam algorithm that allows for overlapping communications and computations, prove its convergence, and propose an accumulation technique to mitigate the high variance caused by small local batch sizes. We deploy the proposed approach in clusters with up to 64 GPUs and demonstrate its practicality and advantages in both runtime and generalization performance under a fixed iteration budget.

Nonconvex Federated Learning on Compact Smooth Submanifolds With Heterogeneous Data

Many machine learning tasks, such as principal component analysis and low-rank matrix completion, give rise to manifold optimization problems. Although there is a large body of work studying the design and analysis of algorithms for manifold optimization in the centralized setting, there are currently very few works addressing the federated setting. In this paper, we consider nonconvex federated learning over a compact smooth submanifold in the setting of heterogeneous client data. We propose an algorithm that leverages stochastic Riemannian gradients and a manifold projection operator to improve computational efficiency, uses local updates to improve communication efficiency, and avoids client drift. Theoretically, we show that our proposed algorithm converges sub-linearly to a neighborhood of a first-order optimal solution by using a novel analysis that jointly exploits the manifold structure and properties of the loss functions. Numerical experiments demonstrate that our algorithm has significantly smaller computational and communication overhead than existing methods.

Differentially Private Online Federated Learning with Correlated Noise

We propose a novel differentially private algorithm for online federated learning that employs temporally correlated noise to improve the utility while ensuring the privacy of the continuously released models. To address challenges stemming from DP noise and local updates with streaming noniid data, we develop a perturbed iterate analysis to control the impact of the DP noise on the utility. Moreover, we demonstrate how the drift errors from local updates can be effectively managed under a quasi-strong convexity condition. Subject to an $(\epsilon, \delta)$-DP budget, we establish a dynamic regret bound over the entire time horizon that quantifies the impact of key parameters and the intensity of changes in dynamic environments. Numerical experiments validate the efficacy of the proposed algorithm.

Composite federated learning with heterogeneous data

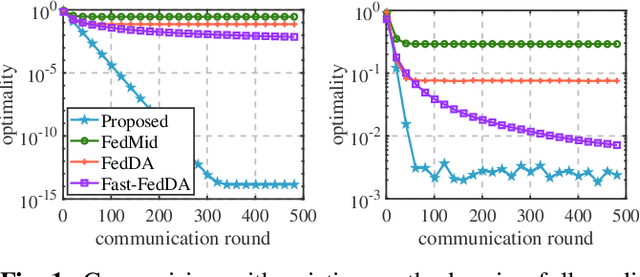
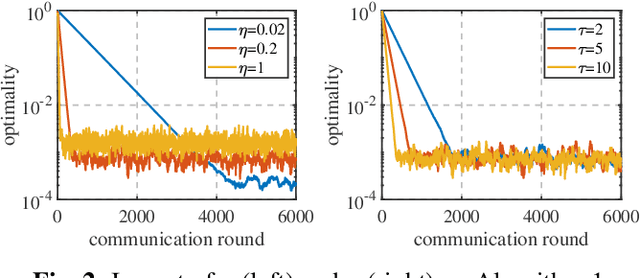
We propose a novel algorithm for solving the composite Federated Learning (FL) problem. This algorithm manages non-smooth regularization by strategically decoupling the proximal operator and communication, and addresses client drift without any assumptions about data similarity. Moreover, each worker uses local updates to reduce the communication frequency with the server and transmits only a $d$-dimensional vector per communication round. We prove that our algorithm converges linearly to a neighborhood of the optimal solution and demonstrate the superiority of our algorithm over state-of-the-art methods in numerical experiments.

Dynamic Privacy Allocation for Locally Differentially Private Federated Learning with Composite Objectives

This paper proposes a locally differentially private federated learning algorithm for strongly convex but possibly nonsmooth problems that protects the gradients of each worker against an honest but curious server. The proposed algorithm adds artificial noise to the shared information to ensure privacy and dynamically allocates the time-varying noise variance to minimize an upper bound of the optimization error subject to a predefined privacy budget constraint. This allows for an arbitrarily large but finite number of iterations to achieve both privacy protection and utility up to a neighborhood of the optimal solution, removing the need for tuning the number of iterations. Numerical results show the superiority of the proposed algorithm over state-of-the-art methods.

MPS-AMS: Masked Patches Selection and Adaptive Masking Strategy Based Self-Supervised Medical Image Segmentation

Existing self-supervised learning methods based on contrastive learning and masked image modeling have demonstrated impressive performances. However, current masked image modeling methods are mainly utilized in natural images, and their applications in medical images are relatively lacking. Besides, their fixed high masking strategy limits the upper bound of conditional mutual information, and the gradient noise is considerable, making less the learned representation information. Motivated by these limitations, in this paper, we propose masked patches selection and adaptive masking strategy based self-supervised medical image segmentation method, named MPS-AMS. We leverage the masked patches selection strategy to choose masked patches with lesions to obtain more lesion representation information, and the adaptive masking strategy is utilized to help learn more mutual information and improve performance further. Extensive experiments on three public medical image segmentation datasets (BUSI, Hecktor, and Brats2018) show that our proposed method greatly outperforms the state-of-the-art self-supervised baselines.