Fast Convergence Rates for Subsampled Natural Gradient Algorithms on Quadratic Model Problems

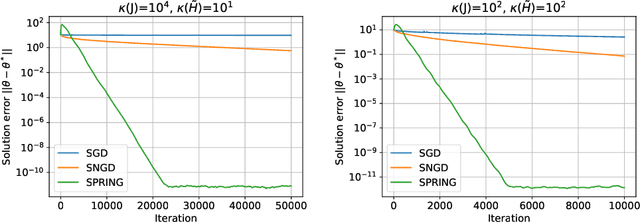
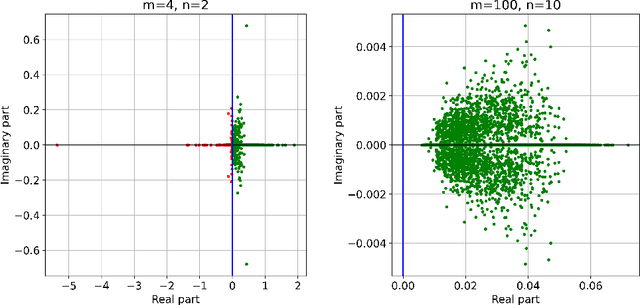
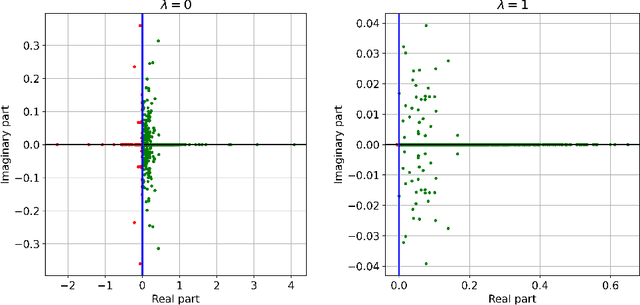
Subsampled natural gradient descent (SNGD) has shown impressive results for parametric optimization tasks in scientific machine learning, such as neural network wavefunctions and physics-informed neural networks, but it has lacked a theoretical explanation. We address this gap by analyzing the convergence of SNGD and its accelerated variant, SPRING, for idealized parametric optimization problems where the model is linear and the loss function is strongly convex and quadratic. In the special case of a least-squares loss, namely the standard linear least-squares problem, we prove that SNGD is equivalent to a regularized Kaczmarz method while SPRING is equivalent to an accelerated regularized Kaczmarz method. As a result, by leveraging existing analyses we obtain under mild conditions (i) the first fast convergence rate for SNGD, (ii) the first convergence guarantee for SPRING in any setting, and (iii) the first proof that SPRING can accelerate SNGD. In the case of a general strongly convex quadratic loss, we extend the analysis of the regularized Kaczmarz method to obtain a fast convergence rate for SNGD under stronger conditions, providing the first explanation for the effectiveness of SNGD outside of the least-squares setting. Overall, our results illustrate how tools from randomized linear algebra can shed new light on the interplay between subsampling and curvature-aware optimization strategies.

Structural Effect and Spectral Enhancement of High-Dimensional Regularized Linear Discriminant Analysis

Regularized linear discriminant analysis (RLDA) is a widely used tool for classification and dimensionality reduction, but its performance in high-dimensional scenarios is inconsistent. Existing theoretical analyses of RLDA often lack clear insight into how data structure affects classification performance. To address this issue, we derive a non-asymptotic approximation of the misclassification rate and thus analyze the structural effect and structural adjustment strategies of RLDA. Based on this, we propose the Spectral Enhanced Discriminant Analysis (SEDA) algorithm, which optimizes the data structure by adjusting the spiked eigenvalues of the population covariance matrix. By developing a new theoretical result on eigenvectors in random matrix theory, we derive an asymptotic approximation on the misclassification rate of SEDA. The bias correction algorithm and parameter selection strategy are then obtained. Experiments on synthetic and real datasets show that SEDA achieves higher classification accuracy and dimensionality reduction compared to existing LDA methods.

BugGen: A Self-Correcting Multi-Agent LLM Pipeline for Realistic RTL Bug Synthesis

Hardware complexity continues to strain verification resources, motivating the adoption of machine learning (ML) methods to improve debug efficiency. However, ML-assisted debugging critically depends on diverse and scalable bug datasets, which existing manual or automated bug insertion methods fail to reliably produce. We introduce BugGen, a first of its kind, fully autonomous, multi-agent pipeline leveraging Large Language Models (LLMs) to systematically generate, insert, and validate realistic functional bugs in RTL. BugGen partitions modules, selects mutation targets via a closed-loop agentic architecture, and employs iterative refinement and rollback mechanisms to ensure syntactic correctness and functional detectability. Evaluated across five OpenTitan IP blocks, BugGen produced 500 unique bugs with 94% functional accuracy and achieved a throughput of 17.7 validated bugs per hour-over five times faster than typical manual expert insertion. Additionally, BugGen identified 104 previously undetected bugs in OpenTitan regressions, highlighting its utility in exposing verification coverage gaps. Compared against Certitude, BugGen demonstrated over twice the syntactic accuracy, deeper exposure of testbench blind spots, and more functionally meaningful and complex bug scenarios. Furthermore, when these BugGen-generated datasets were employed to train ML-based failure triage models, we achieved high classification accuracy (88.1%-93.2%) across different IP blocks, confirming the practical utility and realism of generated bugs. BugGen thus provides a scalable solution for generating high-quality bug datasets, significantly enhancing verification efficiency and ML-assisted debugging.

Non-convex composite federated learning with heterogeneous data

We propose an innovative algorithm for non-convex composite federated learning that decouples the proximal operator evaluation and the communication between server and clients. Moreover, each client uses local updates to communicate less frequently with the server, sends only a single d-dimensional vector per communication round, and overcomes issues with client drift. In the analysis, challenges arise from the use of decoupling strategies and local updates in the algorithm, as well as from the non-convex and non-smooth nature of the problem. We establish sublinear and linear convergence to a bounded residual error under general non-convexity and the proximal Polyak-Lojasiewicz inequality, respectively. In the numerical experiments, we demonstrate the superiority of our algorithm over state-of-the-art methods on both synthetic and real datasets.

Worth Their Weight: Randomized and Regularized Block Kaczmarz Algorithms without Preprocessing

Due to the ever growing amounts of data leveraged for machine learning and scientific computing, it is increasingly important to develop algorithms that sample only a small portion of the data at a time. In the case of linear least-squares, the randomized block Kaczmarz method (RBK) is an appealing example of such an algorithm, but its convergence is only understood under sampling distributions that require potentially prohibitively expensive preprocessing steps. To address this limitation, we analyze RBK when the data is sampled uniformly, showing that its iterates converge in a Monte Carlo sense to a $\textit{weighted}$ least-squares solution. Unfortunately, for general problems the condition number of the weight matrix and the variance of the iterates can become arbitrarily large. We resolve these issues by incorporating regularization into the RBK iterations. Numerical experiments, including examples arising from natural gradient optimization, suggest that the regularized algorithm, ReBlocK, outperforms minibatch stochastic gradient descent for realistic problems that exhibit fast singular value decay.

A Survey of Research in Large Language Models for Electronic Design Automation

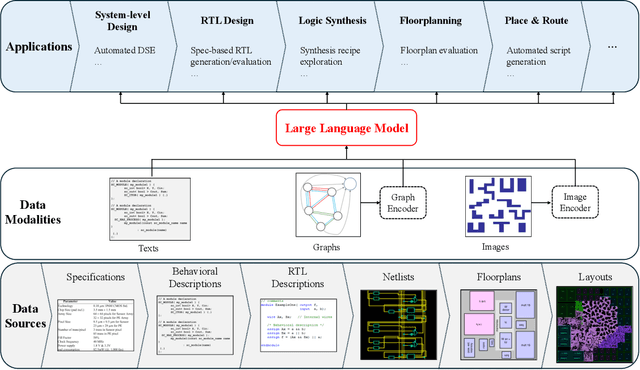
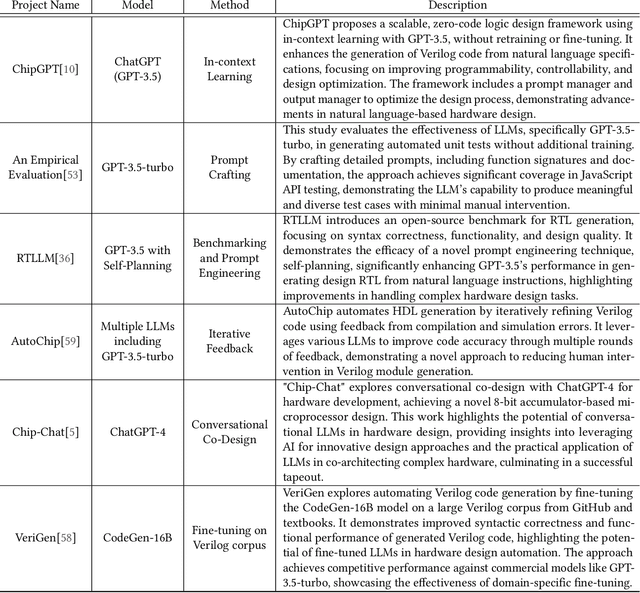
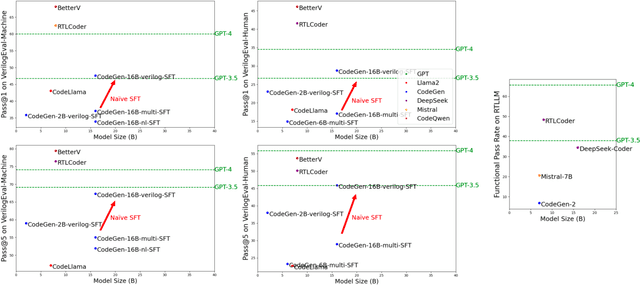
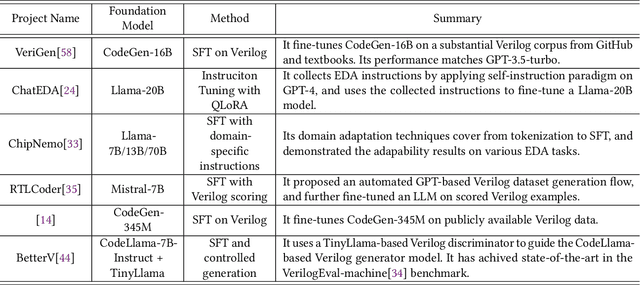
Within the rapidly evolving domain of Electronic Design Automation (EDA), Large Language Models (LLMs) have emerged as transformative technologies, offering unprecedented capabilities for optimizing and automating various aspects of electronic design. This survey provides a comprehensive exploration of LLM applications in EDA, focusing on advancements in model architectures, the implications of varying model sizes, and innovative customization techniques that enable tailored analytical insights. By examining the intersection of LLM capabilities and EDA requirements, the paper highlights the significant impact these models have on extracting nuanced understandings from complex datasets. Furthermore, it addresses the challenges and opportunities in integrating LLMs into EDA workflows, paving the way for future research and application in this dynamic field. Through this detailed analysis, the survey aims to offer valuable insights to professionals in the EDA industry, AI researchers, and anyone interested in the convergence of advanced AI technologies and electronic design.

PatternPaint: Generating Layout Patterns Using Generative AI and Inpainting Techniques

Generation of VLSI layout patterns is essential for a wide range of Design For Manufacturability (DFM) studies. In this study, we investigate the potential of generative machine learning models for creating design rule legal metal layout patterns. Our results demonstrate that the proposed model can generate legal patterns in complex design rule settings and achieves a high diversity score. The designed system, with its flexible settings, supports both pattern generation with localized changes, and design rule violation correction. Our methodology is validated on Intel 18A Process Design Kit (PDK) and can produce a wide range of DRC-compliant pattern libraries with only 20 starter patterns.

Nonconvex Federated Learning on Compact Smooth Submanifolds With Heterogeneous Data

Many machine learning tasks, such as principal component analysis and low-rank matrix completion, give rise to manifold optimization problems. Although there is a large body of work studying the design and analysis of algorithms for manifold optimization in the centralized setting, there are currently very few works addressing the federated setting. In this paper, we consider nonconvex federated learning over a compact smooth submanifold in the setting of heterogeneous client data. We propose an algorithm that leverages stochastic Riemannian gradients and a manifold projection operator to improve computational efficiency, uses local updates to improve communication efficiency, and avoids client drift. Theoretically, we show that our proposed algorithm converges sub-linearly to a neighborhood of a first-order optimal solution by using a novel analysis that jointly exploits the manifold structure and properties of the loss functions. Numerical experiments demonstrate that our algorithm has significantly smaller computational and communication overhead than existing methods.

AdaFish: Fast low-rank parameter-efficient fine-tuning by using second-order information

Recent advancements in large-scale pretrained models have significantly improved performance across a variety of tasks in natural language processing and computer vision. However, the extensive number of parameters in these models necessitates substantial memory and computational resources for full training. To adapt these models for downstream tasks or specific application-oriented datasets, parameter-efficient fine-tuning methods leveraging pretrained parameters have gained considerable attention. However, it can still be time-consuming due to lots of parameters and epochs. In this work, we introduce AdaFish, an efficient algorithm of the second-order type designed to expedite the training process within low-rank decomposition-based fine-tuning frameworks. Our key observation is that the associated generalized Fisher information matrix is either low-rank or extremely small-scaled. Such a generalized Fisher information matrix is shown to be equivalent to the Hessian matrix. Moreover, we prove the global convergence of AdaFish, along with its iteration/oracle complexity. Numerical experiments show that our algorithm is quite competitive with the state-of-the-art AdamW method.

MediViSTA-SAM: Zero-shot Medical Video Analysis with Spatio-temporal SAM Adaptation

In recent years, the Segmentation Anything Model (SAM) has attracted considerable attention as a foundational model well-known for its robust generalization capabilities across various downstream tasks. However, SAM does not exhibit satisfactory performance in the realm of medical image analysis. In this study, we introduce the first study on adapting SAM on video segmentation, called MediViSTA-SAM, a novel approach designed for medical video segmentation. Given video data, MediViSTA, spatio-temporal adapter captures long and short range temporal attention with cross-frame attention mechanism effectively constraining it to consider the immediately preceding video frame as a reference, while also considering spatial information effectively. Additionally, it incorporates multi-scale fusion by employing a U-shaped encoder and a modified mask decoder to handle objects of varying sizes. To evaluate our approach, extensive experiments were conducted using state-of-the-art (SOTA) methods, assessing its generalization abilities on multi-vendor in-house echocardiography datasets. The results highlight the accuracy and effectiveness of our network in medical video segmentation.