Gil Goldshlager
Fast Convergence Rates for Subsampled Natural Gradient Algorithms on Quadratic Model Problems
Aug 28, 2025
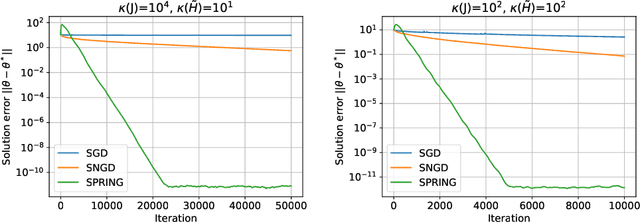
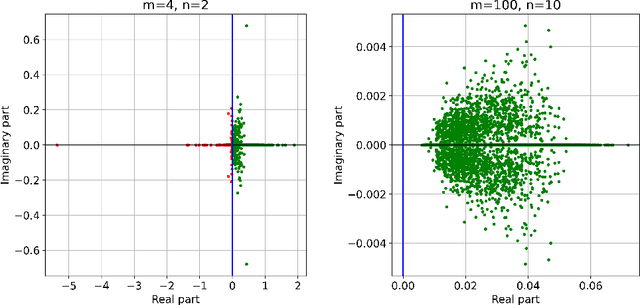
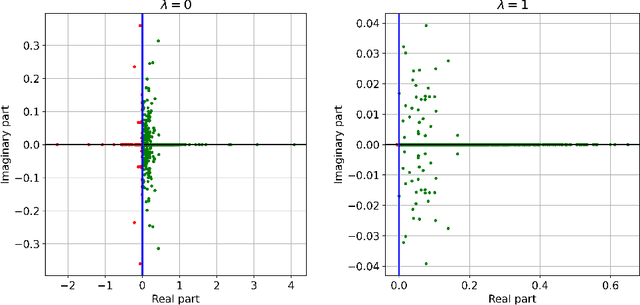
Abstract:Subsampled natural gradient descent (SNGD) has shown impressive results for parametric optimization tasks in scientific machine learning, such as neural network wavefunctions and physics-informed neural networks, but it has lacked a theoretical explanation. We address this gap by analyzing the convergence of SNGD and its accelerated variant, SPRING, for idealized parametric optimization problems where the model is linear and the loss function is strongly convex and quadratic. In the special case of a least-squares loss, namely the standard linear least-squares problem, we prove that SNGD is equivalent to a regularized Kaczmarz method while SPRING is equivalent to an accelerated regularized Kaczmarz method. As a result, by leveraging existing analyses we obtain under mild conditions (i) the first fast convergence rate for SNGD, (ii) the first convergence guarantee for SPRING in any setting, and (iii) the first proof that SPRING can accelerate SNGD. In the case of a general strongly convex quadratic loss, we extend the analysis of the regularized Kaczmarz method to obtain a fast convergence rate for SNGD under stronger conditions, providing the first explanation for the effectiveness of SNGD outside of the least-squares setting. Overall, our results illustrate how tools from randomized linear algebra can shed new light on the interplay between subsampling and curvature-aware optimization strategies.
Improving Energy Natural Gradient Descent through Woodbury, Momentum, and Randomization
May 17, 2025Abstract:Natural gradient methods significantly accelerate the training of Physics-Informed Neural Networks (PINNs), but are often prohibitively costly. We introduce a suite of techniques to improve the accuracy and efficiency of energy natural gradient descent (ENGD) for PINNs. First, we leverage the Woodbury formula to dramatically reduce the computational complexity of ENGD. Second, we adapt the Subsampled Projected-Increment Natural Gradient Descent algorithm from the variational Monte Carlo literature to accelerate the convergence. Third, we explore the use of randomized algorithms to further reduce the computational cost in the case of large batch sizes. We find that randomization accelerates progress in the early stages of training for low-dimensional problems, and we identify key barriers to attaining acceleration in other scenarios. Our numerical experiments demonstrate that our methods outperform previous approaches, achieving the same $L^2$ error as the original ENGD up to $75\times$ faster.
Worth Their Weight: Randomized and Regularized Block Kaczmarz Algorithms without Preprocessing
Feb 02, 2025



Abstract:Due to the ever growing amounts of data leveraged for machine learning and scientific computing, it is increasingly important to develop algorithms that sample only a small portion of the data at a time. In the case of linear least-squares, the randomized block Kaczmarz method (RBK) is an appealing example of such an algorithm, but its convergence is only understood under sampling distributions that require potentially prohibitively expensive preprocessing steps. To address this limitation, we analyze RBK when the data is sampled uniformly, showing that its iterates converge in a Monte Carlo sense to a $\textit{weighted}$ least-squares solution. Unfortunately, for general problems the condition number of the weight matrix and the variance of the iterates can become arbitrarily large. We resolve these issues by incorporating regularization into the RBK iterations. Numerical experiments, including examples arising from natural gradient optimization, suggest that the regularized algorithm, ReBlocK, outperforms minibatch stochastic gradient descent for realistic problems that exhibit fast singular value decay.
A Kaczmarz-inspired approach to accelerate the optimization of neural network wavefunctions
Jan 18, 2024



Abstract:Neural network wavefunctions optimized using the variational Monte Carlo method have been shown to produce highly accurate results for the electronic structure of atoms and small molecules, but the high cost of optimizing such wavefunctions prevents their application to larger systems. We propose the Subsampled Projected-Increment Natural Gradient Descent (SPRING) optimizer to reduce this bottleneck. SPRING combines ideas from the recently introduced minimum-step stochastic reconfiguration optimizer (MinSR) and the classical randomized Kaczmarz method for solving linear least-squares problems. We demonstrate that SPRING outperforms both MinSR and the popular Kronecker-Factored Approximate Curvature method (KFAC) across a number of small atoms and molecules, given that the learning rates of all methods are optimally tuned. For example, on the oxygen atom, SPRING attains chemical accuracy after forty thousand training iterations, whereas both MinSR and KFAC fail to do so even after one hundred thousand iterations.
Convergence of stochastic gradient descent on parameterized sphere with applications to variational Monte Carlo simulation
Mar 24, 2023



Abstract:We analyze stochastic gradient descent (SGD) type algorithms on a high-dimensional sphere which is parameterized by a neural network up to a normalization constant. We provide a new algorithm for the setting of supervised learning and show its convergence both theoretically and numerically. We also provide the first proof of convergence for the unsupervised setting, which corresponds to the widely used variational Monte Carlo (VMC) method in quantum physics.
Explicitly antisymmetrized neural network layers for variational Monte Carlo simulation
Dec 07, 2021



Abstract:The combination of neural networks and quantum Monte Carlo methods has arisen as a path forward for highly accurate electronic structure calculations. Previous proposals have combined equivariant neural network layers with an antisymmetric layer to satisfy the antisymmetry requirements of the electronic wavefunction. However, to date it is unclear if one can represent antisymmetric functions of physical interest, and it is difficult to measure the expressiveness of the antisymmetric layer. This work attempts to address this problem by introducing explicitly antisymmetrized universal neural network layers as a diagnostic tool. We first introduce a generic antisymmetric (GA) layer, which we use to replace the entire antisymmetric layer of the highly accurate ansatz known as the FermiNet. We demonstrate that the resulting FermiNet-GA architecture can yield effectively the exact ground state energy for small systems. We then consider a factorized antisymmetric (FA) layer which more directly generalizes the FermiNet by replacing products of determinants with products of antisymmetrized neural networks. Interestingly, the resulting FermiNet-FA architecture does not outperform the FermiNet. This suggests that the sum of products of antisymmetries is a key limiting aspect of the FermiNet architecture. To explore this further, we investigate a slight modification of the FermiNet called the full determinant mode, which replaces each product of determinants with a single combined determinant. The full single-determinant FermiNet closes a large part of the gap between the standard single-determinant FermiNet and FermiNet-GA. Surprisingly, on the nitrogen molecule at a dissociating bond length of 4.0 Bohr, the full single-determinant FermiNet can significantly outperform the standard 64-determinant FermiNet, yielding an energy within 0.4 kcal/mol of the best available computational benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge