SAIL-Embedding Technical Report: Omni-modal Embedding Foundation Model

Multimodal embedding models aim to yield informative unified representations that empower diverse cross-modal tasks. Despite promising developments in the evolution from CLIP-based dual-tower architectures to large vision-language models, prior works still face unavoidable challenges in real-world applications and business scenarios, such as the limited modality support, unstable training mechanisms, and industrial domain gaps. In this work, we introduce SAIL-Embedding, an omni-modal embedding foundation model that addresses these issues through tailored training strategies and architectural design. In the optimization procedure, we propose a multi-stage training scheme to boost the multifaceted effectiveness of representation learning. Specifically, the content-aware progressive training aims to enhance the model's adaptability to diverse downstream tasks and master enriched cross-modal proficiency. The collaboration-aware recommendation enhancement training further adapts multimodal representations for recommendation scenarios by distilling knowledge from sequence-to-item and ID-to-item embeddings while mining user historical interests. Concurrently, we develop the stochastic specialization and dataset-driven pattern matching to strengthen model training flexibility and generalizability. Experimental results show that SAIL-Embedding achieves SOTA performance compared to other methods in different retrieval tasks. In online experiments across various real-world scenarios integrated with our model, we observe a significant increase in Lifetime (LT), which is a crucial indicator for the recommendation experience. For instance, the model delivers the 7-day LT gain of +0.158% and the 14-day LT gain of +0.144% in the Douyin-Selected scenario. For the Douyin feed rank model, the match features produced by SAIL-Embedding yield a +0.08% AUC gain.

Fast Convergence Rates for Subsampled Natural Gradient Algorithms on Quadratic Model Problems

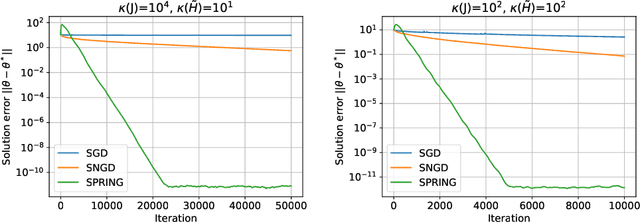
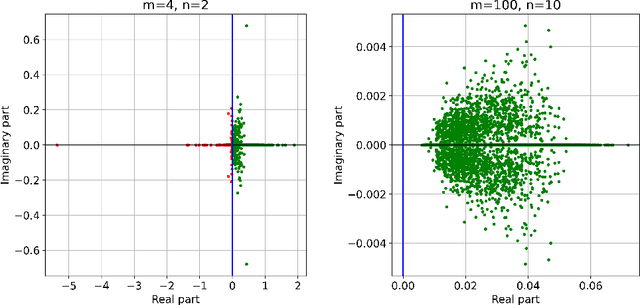
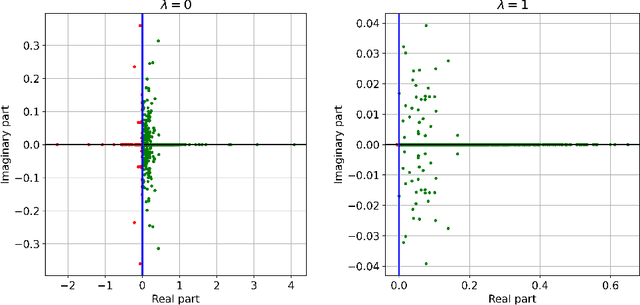
Subsampled natural gradient descent (SNGD) has shown impressive results for parametric optimization tasks in scientific machine learning, such as neural network wavefunctions and physics-informed neural networks, but it has lacked a theoretical explanation. We address this gap by analyzing the convergence of SNGD and its accelerated variant, SPRING, for idealized parametric optimization problems where the model is linear and the loss function is strongly convex and quadratic. In the special case of a least-squares loss, namely the standard linear least-squares problem, we prove that SNGD is equivalent to a regularized Kaczmarz method while SPRING is equivalent to an accelerated regularized Kaczmarz method. As a result, by leveraging existing analyses we obtain under mild conditions (i) the first fast convergence rate for SNGD, (ii) the first convergence guarantee for SPRING in any setting, and (iii) the first proof that SPRING can accelerate SNGD. In the case of a general strongly convex quadratic loss, we extend the analysis of the regularized Kaczmarz method to obtain a fast convergence rate for SNGD under stronger conditions, providing the first explanation for the effectiveness of SNGD outside of the least-squares setting. Overall, our results illustrate how tools from randomized linear algebra can shed new light on the interplay between subsampling and curvature-aware optimization strategies.

Operator-Level Quantum Acceleration of Non-Logconcave Sampling

Sampling from probability distributions of the form $\sigma \propto e^{-\beta V}$, where $V$ is a continuous potential, is a fundamental task across physics, chemistry, biology, computer science, and statistics. However, when $V$ is non-convex, the resulting distribution becomes non-logconcave, and classical methods such as Langevin dynamics often exhibit poor performance. We introduce the first quantum algorithm that provably accelerates a broad class of continuous-time sampling dynamics. For Langevin dynamics, our method encodes the target Gibbs measure into the amplitudes of a quantum state, identified as the kernel of a block matrix derived from a factorization of the Witten Laplacian operator. This connection enables Gibbs sampling via singular value thresholding and yields the first provable quantum advantage with respect to the Poincar\'e constant in the non-logconcave setting. Building on this framework, we further develop the first quantum algorithm that accelerates replica exchange Langevin diffusion, a widely used method for sampling from complex, rugged energy landscapes.

MathMistake Checker: A Comprehensive Demonstration for Step-by-Step Math Problem Mistake Finding by Prompt-Guided LLMs

We propose a novel system, MathMistake Checker, designed to automate step-by-step mistake finding in mathematical problems with lengthy answers through a two-stage process. The system aims to simplify grading, increase efficiency, and enhance learning experiences from a pedagogical perspective. It integrates advanced technologies, including computer vision and the chain-of-thought capabilities of the latest large language models (LLMs). Our system supports open-ended grading without reference answers and promotes personalized learning by providing targeted feedback. We demonstrate its effectiveness across various types of math problems, such as calculation and word problems.

Worth Their Weight: Randomized and Regularized Block Kaczmarz Algorithms without Preprocessing

Due to the ever growing amounts of data leveraged for machine learning and scientific computing, it is increasingly important to develop algorithms that sample only a small portion of the data at a time. In the case of linear least-squares, the randomized block Kaczmarz method (RBK) is an appealing example of such an algorithm, but its convergence is only understood under sampling distributions that require potentially prohibitively expensive preprocessing steps. To address this limitation, we analyze RBK when the data is sampled uniformly, showing that its iterates converge in a Monte Carlo sense to a $\textit{weighted}$ least-squares solution. Unfortunately, for general problems the condition number of the weight matrix and the variance of the iterates can become arbitrarily large. We resolve these issues by incorporating regularization into the RBK iterations. Numerical experiments, including examples arising from natural gradient optimization, suggest that the regularized algorithm, ReBlocK, outperforms minibatch stochastic gradient descent for realistic problems that exhibit fast singular value decay.

Constructing Cell-type Taxonomy by Optimal Transport with Relaxed Marginal Constraints

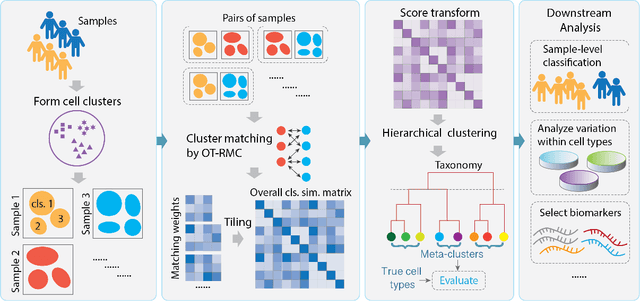
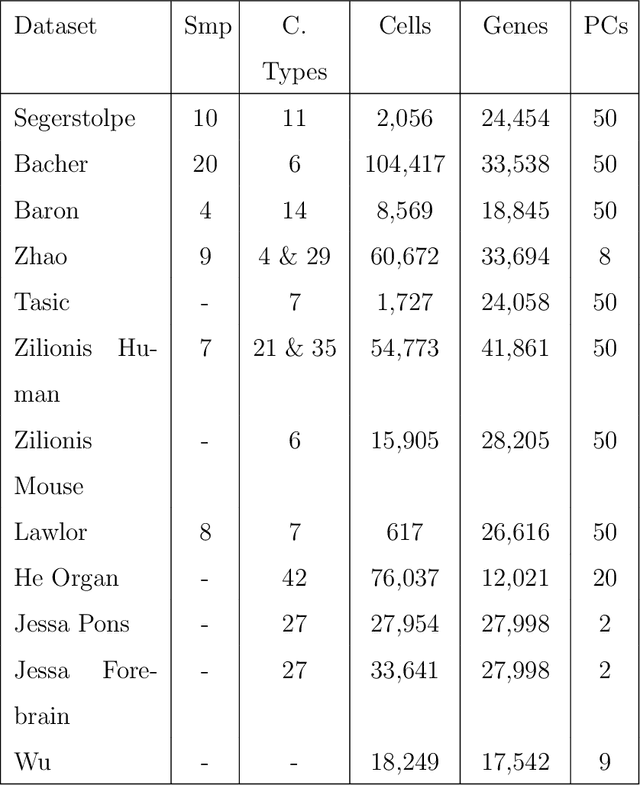
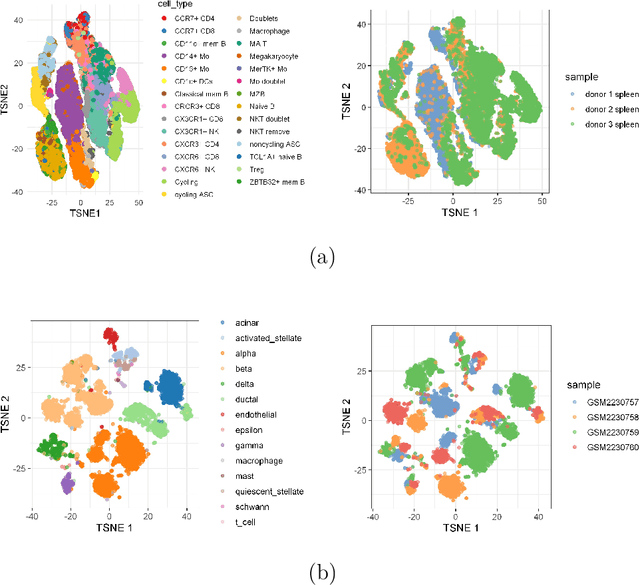
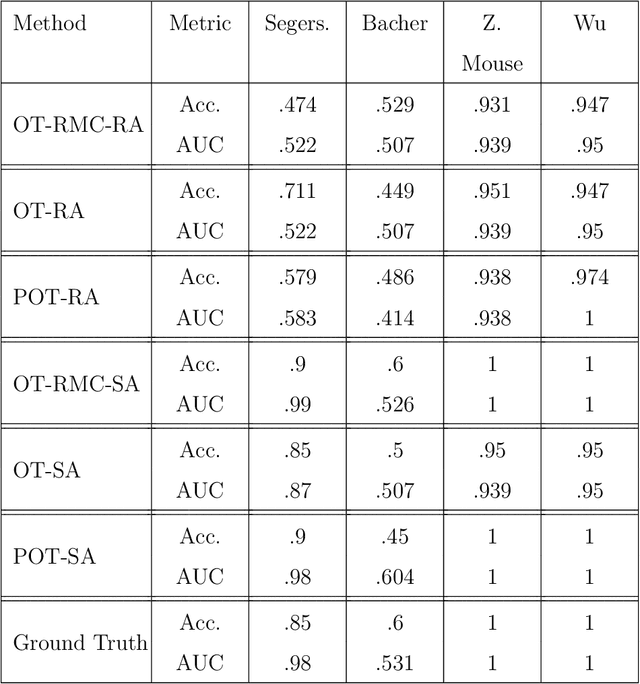
The rapid emergence of single-cell data has facilitated the study of many different biological conditions at the cellular level. Cluster analysis has been widely applied to identify cell types, capturing the essential patterns of the original data in a much more concise form. One challenge in the cluster analysis of cells is matching clusters extracted from datasets of different origins or conditions. Many existing algorithms cannot recognize new cell types present in only one of the two samples when establishing a correspondence between clusters obtained from two samples. Additionally, when there are more than two samples, it is advantageous to align clusters across all samples simultaneously rather than performing pairwise alignment. Our approach aims to construct a taxonomy for cell clusters across all samples to better annotate these clusters and effectively extract features for downstream analysis. A new system for constructing cell-type taxonomy has been developed by combining the technique of Optimal Transport with Relaxed Marginal Constraints (OT-RMC) and the simultaneous alignment of clusters across multiple samples. OT-RMC allows us to address challenges that arise when the proportions of clusters vary substantially between samples or when some clusters do not appear in all the samples. Experiments on more than twenty datasets demonstrate that the taxonomy constructed by this new system can yield highly accurate annotation of cell types. Additionally, sample-level features extracted based on the taxonomy result in accurate classification of samples.

RAG4ITOps: A Supervised Fine-Tunable and Comprehensive RAG Framework for IT Operations and Maintenance

With the ever-increasing demands on Question Answering (QA) systems for IT operations and maintenance, an efficient and supervised fine-tunable framework is necessary to ensure the data security, private deployment and continuous upgrading. Although Large Language Models (LLMs) have notably improved the open-domain QA's performance, how to efficiently handle enterprise-exclusive corpora and build domain-specific QA systems are still less-studied for industrial applications. In this paper, we propose a general and comprehensive framework based on Retrieval Augmented Generation (RAG) and facilitate the whole business process of establishing QA systems for IT operations and maintenance. In accordance with the prevailing RAG method, our proposed framework, named with RAG4ITOps, composes of two major stages: (1) Models Fine-tuning \& Data Vectorization, and (2) Online QA System Process. At the Stage 1, we leverage a contrastive learning method with two negative sampling strategies to fine-tune the embedding model, and design the instruction templates to fine-tune the LLM with a Retrieval Augmented Fine-Tuning method. At the Stage 2, an efficient process of QA system is built for serving. We collect enterprise-exclusive corpora from the domain of cloud computing, and the extensive experiments show that our method achieves superior results than counterparts on two kinds of QA tasks. Our experiment also provide a case for applying the RAG4ITOps to real-world enterprise-level applications.

Costal Cartilage Segmentation with Topology Guided Deformable Mamba: Method and Benchmark

Costal cartilage segmentation is crucial to various medical applications, necessitating precise and reliable techniques due to its complex anatomy and the importance of accurate diagnosis and surgical planning. We propose a novel deep learning-based approach called topology-guided deformable Mamba (TGDM) for costal cartilage segmentation. The TGDM is tailored to capture the intricate long-range costal cartilage relationships. Our method leverages a deformable model that integrates topological priors to enhance the adaptability and accuracy of the segmentation process. Furthermore, we developed a comprehensive benchmark that contains 165 cases for costal cartilage segmentation. This benchmark sets a new standard for evaluating costal cartilage segmentation techniques and provides a valuable resource for future research. Extensive experiments conducted on both in-domain benchmarks and out-of domain test sets demonstrate the superiority of our approach over existing methods, showing significant improvements in segmentation precision and robustness.

Canonical Variates in Wasserstein Metric Space

In this paper, we address the classification of instances each characterized not by a singular point, but by a distribution on a vector space. We employ the Wasserstein metric to measure distances between distributions, which are then used by distance-based classification algorithms such as k-nearest neighbors, k-means, and pseudo-mixture modeling. Central to our investigation is dimension reduction within the Wasserstein metric space to enhance classification accuracy. We introduce a novel approach grounded in the principle of maximizing Fisher's ratio, defined as the quotient of between-class variation to within-class variation. The directions in which this ratio is maximized are termed discriminant coordinates or canonical variates axes. In practice, we define both between-class and within-class variations as the average squared distances between pairs of instances, with the pairs either belonging to the same class or to different classes. This ratio optimization is achieved through an iterative algorithm, which alternates between optimal transport and maximization steps within the vector space. We conduct empirical studies to assess the algorithm's convergence and, through experimental validation, demonstrate that our dimension reduction technique substantially enhances classification performance. Moreover, our method outperforms well-established algorithms that operate on vector representations derived from distributional data. It also exhibits robustness against variations in the distributional representations of data clouds.

The ESPRIT algorithm under high noise: Optimal error scaling and noisy super-resolution

Subspace-based signal processing techniques, such as the Estimation of Signal Parameters via Rotational Invariant Techniques (ESPRIT) algorithm, are popular methods for spectral estimation. These algorithms can achieve the so-called super-resolution scaling under low noise conditions, surpassing the well-known Nyquist limit. However, the performance of these algorithms under high-noise conditions is not as well understood. Existing state-of-the-art analysis indicates that ESPRIT and related algorithms can be resilient even for signals where each observation is corrupted by statistically independent, mean-zero noise of size $\mathcal{O}(1)$, but these analyses only show that the error $\epsilon$ decays at a slow rate $\epsilon=\mathcal{\tilde{O}}(n^{-1/2})$ with respect to the cutoff frequency $n$. In this work, we prove that under certain assumptions of bias and high noise, the ESPRIT algorithm can attain a significantly improved error scaling $\epsilon = \mathcal{\tilde{O}}(n^{-3/2})$, exhibiting noisy super-resolution scaling beyond the Nyquist limit. We further establish a theoretical lower bound and show that this scaling is optimal. Our analysis introduces novel matrix perturbation results, which could be of independent interest.