Human2Robot: Learning Robot Actions from Paired Human-Robot Videos

Distilling knowledge from human demonstrations is a promising way for robots to learn and act. Existing work often overlooks the differences between humans and robots, producing unsatisfactory results. In this paper, we study how perfectly aligned human-robot pairs benefit robot learning. Capitalizing on VR-based teleportation, we introduce H\&R, a third-person dataset with 2,600 episodes, each of which captures the fine-grained correspondence between human hands and robot gripper. Inspired by the recent success of diffusion models, we introduce Human2Robot, an end-to-end diffusion framework that formulates learning from human demonstrates as a generative task. Human2Robot fully explores temporal dynamics in human videos to generate robot videos and predict actions at the same time. Through comprehensive evaluations of 8 seen, changed and unseen tasks in real-world settings, we demonstrate that Human2Robot can not only generate high-quality robot videos but also excel in seen tasks and generalize to unseen objects, backgrounds and even new tasks effortlessly.

FNIN: A Fourier Neural Operator-based Numerical Integration Network for Surface-form-gradients

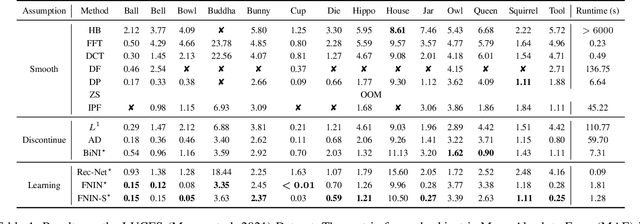
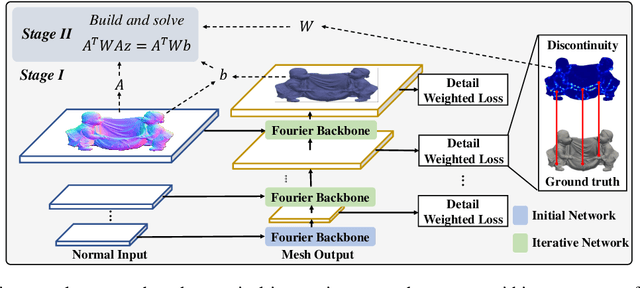
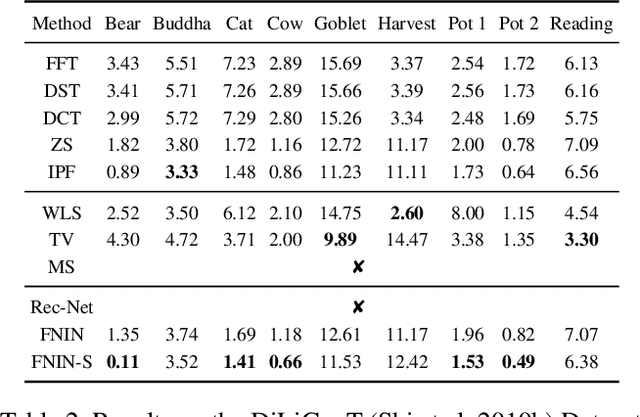
Surface-from-gradients (SfG) aims to recover a three-dimensional (3D) surface from its gradients. Traditional methods encounter significant challenges in achieving high accuracy and handling high-resolution inputs, particularly facing the complex nature of discontinuities and the inefficiencies associated with large-scale linear solvers. Although recent advances in deep learning, such as photometric stereo, have enhanced normal estimation accuracy, they do not fully address the intricacies of gradient-based surface reconstruction. To overcome these limitations, we propose a Fourier neural operator-based Numerical Integration Network (FNIN) within a two-stage optimization framework. In the first stage, our approach employs an iterative architecture for numerical integration, harnessing an advanced Fourier neural operator to approximate the solution operator in Fourier space. Additionally, a self-learning attention mechanism is incorporated to effectively detect and handle discontinuities. In the second stage, we refine the surface reconstruction by formulating a weighted least squares problem, addressing the identified discontinuities rationally. Extensive experiments demonstrate that our method achieves significant improvements in both accuracy and efficiency compared to current state-of-the-art solvers. This is particularly evident in handling high-resolution images with complex data, achieving errors of fewer than 0.1 mm on tested objects.

Differentiable Quantum Computing for Large-scale Linear Control

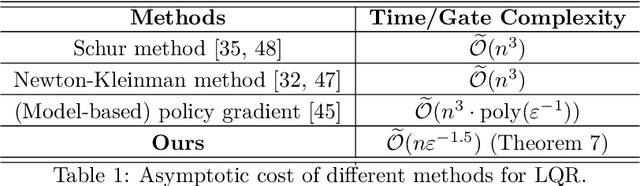
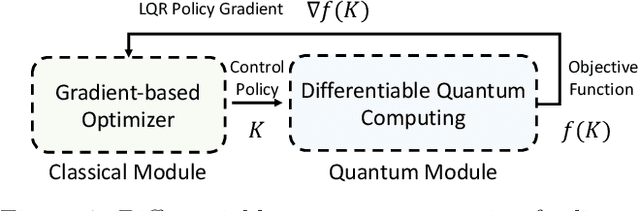
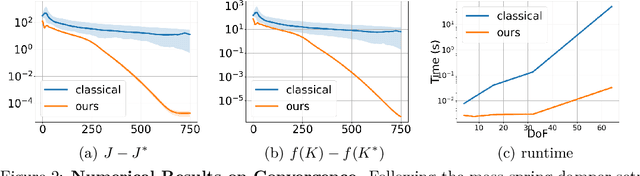
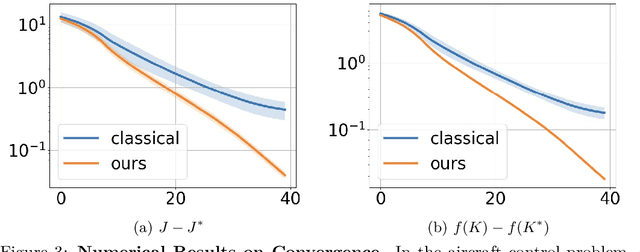
As industrial models and designs grow increasingly complex, the demand for optimal control of large-scale dynamical systems has significantly increased. However, traditional methods for optimal control incur significant overhead as problem dimensions grow. In this paper, we introduce an end-to-end quantum algorithm for linear-quadratic control with provable speedups. Our algorithm, based on a policy gradient method, incorporates a novel quantum subroutine for solving the matrix Lyapunov equation. Specifically, we build a quantum-assisted differentiable simulator for efficient gradient estimation that is more accurate and robust than classical methods relying on stochastic approximation. Compared to the classical approaches, our method achieves a super-quadratic speedup. To the best of our knowledge, this is the first end-to-end quantum application to linear control problems with provable quantum advantage.

A quantum-classical performance separation in nonconvex optimization

In this paper, we identify a family of nonconvex continuous optimization instances, each $d$-dimensional instance with $2^d$ local minima, to demonstrate a quantum-classical performance separation. Specifically, we prove that the recently proposed Quantum Hamiltonian Descent (QHD) algorithm [Leng et al., arXiv:2303.01471] is able to solve any $d$-dimensional instance from this family using $\widetilde{\mathcal{O}}(d^3)$ quantum queries to the function value and $\widetilde{\mathcal{O}}(d^4)$ additional 1-qubit and 2-qubit elementary quantum gates. On the other side, a comprehensive empirical study suggests that representative state-of-the-art classical optimization algorithms/solvers (including Gurobi) would require a super-polynomial time to solve such optimization instances.

Quantum Hamiltonian Descent

Gradient descent is a fundamental algorithm in both theory and practice for continuous optimization. Identifying its quantum counterpart would be appealing to both theoretical and practical quantum applications. A conventional approach to quantum speedups in optimization relies on the quantum acceleration of intermediate steps of classical algorithms, while keeping the overall algorithmic trajectory and solution quality unchanged. We propose Quantum Hamiltonian Descent (QHD), which is derived from the path integral of dynamical systems referring to the continuous-time limit of classical gradient descent algorithms, as a truly quantum counterpart of classical gradient methods where the contribution from classically-prohibited trajectories can significantly boost QHD's performance for non-convex optimization. Moreover, QHD is described as a Hamiltonian evolution efficiently simulatable on both digital and analog quantum computers. By embedding the dynamics of QHD into the evolution of the so-called Quantum Ising Machine (including D-Wave and others), we empirically observe that the D-Wave-implemented QHD outperforms a selection of state-of-the-art gradient-based classical solvers and the standard quantum adiabatic algorithm, based on the time-to-solution metric, on non-convex constrained quadratic programming instances up to 75 dimensions. Finally, we propose a "three-phase picture" to explain the behavior of QHD, especially its difference from the quantum adiabatic algorithm.

Differentiable Analog Quantum Computing for Optimization and Control

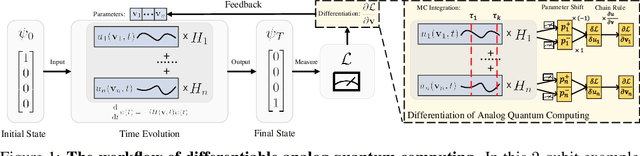
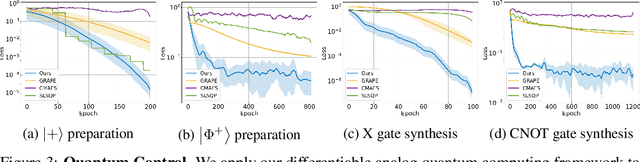
We formulate the first differentiable analog quantum computing framework with a specific parameterization design at the analog signal (pulse) level to better exploit near-term quantum devices via variational methods. We further propose a scalable approach to estimate the gradients of quantum dynamics using a forward pass with Monte Carlo sampling, which leads to a quantum stochastic gradient descent algorithm for scalable gradient-based training in our framework. Applying our framework to quantum optimization and control, we observe a significant advantage of differentiable analog quantum computing against SOTAs based on parameterized digital quantum circuits by orders of magnitude.

Quantum Algorithms for Escaping from Saddle Points

We initiate the study of quantum algorithms for escaping from saddle points with provable guarantee. Given a function $f\colon\mathbb{R}^{n}\to\mathbb{R}$, our quantum algorithm outputs an $\epsilon$-approximate second-order stationary point using $\tilde{O}(\log^{2} n/\epsilon^{1.75})$ queries to the quantum evaluation oracle (i.e., the zeroth-order oracle). Compared to the classical state-of-the-art algorithm by Jin et al. with $\tilde{O}(\log^{6} n/\epsilon^{1.75})$ queries to the gradient oracle (i.e., the first-order oracle), our quantum algorithm is polynomially better in terms of $n$ and matches its complexity in terms of $1/\epsilon$. Our quantum algorithm is built upon two techniques: First, we replace the classical perturbations in gradient descent methods by simulating quantum wave equations, which constitutes the polynomial speedup in $n$ for escaping from saddle points. Second, we show how to use a quantum gradient computation algorithm due to Jordan to replace the classical gradient queries by quantum evaluation queries with the same complexity. Finally, we also perform numerical experiments that support our quantum speedup.