Differentiable Quantum Computing for Large-scale Linear Control

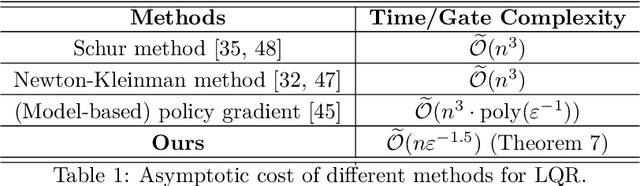
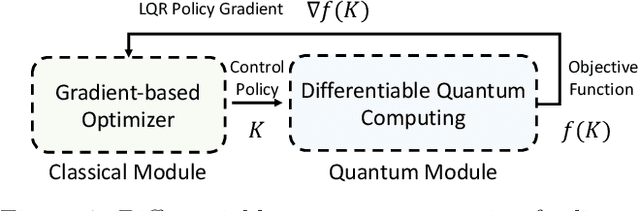
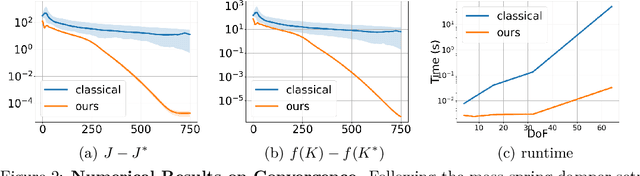
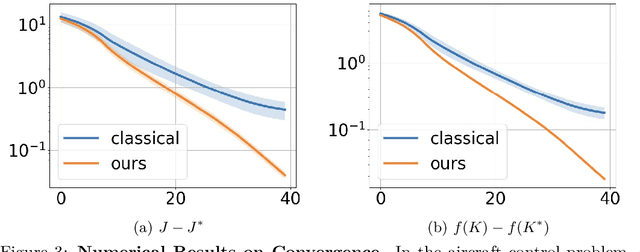
As industrial models and designs grow increasingly complex, the demand for optimal control of large-scale dynamical systems has significantly increased. However, traditional methods for optimal control incur significant overhead as problem dimensions grow. In this paper, we introduce an end-to-end quantum algorithm for linear-quadratic control with provable speedups. Our algorithm, based on a policy gradient method, incorporates a novel quantum subroutine for solving the matrix Lyapunov equation. Specifically, we build a quantum-assisted differentiable simulator for efficient gradient estimation that is more accurate and robust than classical methods relying on stochastic approximation. Compared to the classical approaches, our method achieves a super-quadratic speedup. To the best of our knowledge, this is the first end-to-end quantum application to linear control problems with provable quantum advantage.

ButterflyNet2D: Bridging Classical Methods and Neural Network Methods in Image Processing

Both classical Fourier transform-based methods and neural network methods are widely used in image processing tasks. The former has better interpretability, whereas the latter often achieves better performance in practice. This paper introduces ButterflyNet2D, a regular CNN with sparse cross-channel connections. A Fourier initialization strategy for ButterflyNet2D is proposed to approximate Fourier transforms. Numerical experiments validate the accuracy of ButterflyNet2D approximating both the Fourier and the inverse Fourier transforms. Moreover, through four image processing tasks and image datasets, we show that training ButterflyNet2D from Fourier initialization does achieve better performance than random initialized neural networks.