Finding Stationary Points by Comparisons

We study the problem of finding stationary points of non-convex functions when access to the objective is provided only through a comparison oracle that, given two points, outputs which has the larger function value. For a twice differentiable $f\colon\mathbb R^n\to\mathbb R$ with Lipschitz gradient and Hessian, we develop an algorithm that visits an $ε$-stationary point using $\widetilde O(n^2/ε^{1.5})$ queries. Our approach uses a subroutine that estimates the normalized Hessian to accuracy $δ$ using $\widetilde O(n^2\log(1/δ))$ queries. We further study this problem with a quantum comparison oracle model where queries can be made in superpositions, and develop the first quantum algorithm that finds an $ε$-stationary point, which takes $\widetilde O(n/ε^{1.5})$ queries.

Beyond the Blood Draw: Explainable Machine Learning for Non-Invasive Dysglycemia Risk Screening

Dysglycemia, encompassing both prediabetes and diabetes, affects huge numbers of adults worldwide, yet many of them remain undiagnosed. We developed and validated machine-learning (ML) models for non-invasive screening of dysglycemia risk that require no laboratory tests. Pooling data from the National Health and Nutrition Examination Survey (NHANES) 2017--2023 (n=14,352), we trained six ML models with stratified 5-fold cross-validation and compared them with two established clinical risk scores. LightGBM achieved the highest area under the receiver operating characteristic curve (AUC=0.820, 95% CI: 0.806--0.835), outperforming the Finnish Diabetes Risk Score (0.745) and American Diabetes Association Risk Test (0.783). SHAP analysis identified age, race/ethnicity, and waist-to-height ratio as the most influential predictors. Subgroup analyses confirmed consistent performance across demographic strata (AUC: 0.735--0.832). These results demonstrate the feasibility of explainable, laboratory-free dysglycemia screening for deployment in community settings and self-tracking health applications.

Anomaly Detection Based on Critical Paths for Deep Neural Networks

Deep neural networks (DNNs) are notoriously hard to understand and difficult to defend. Extracting representative paths (including the neuron activation values and the connections between neurons) from DNNs using software engineering approaches has recently shown to be a promising approach in interpreting the decision making process of blackbox DNNs, as the extracted paths are often effective in capturing essential features. With this in mind, this work investigates a novel approach that extracts critical paths from DNNs and subsequently applies the extracted paths for the anomaly detection task, based on the observation that outliers and adversarial inputs do not usually induce the same activation pattern on those paths as normal (in-distribution) inputs. In our approach, we first identify critical detection paths via genetic evolution and mutation. Since different paths in a DNN often capture different features for the same target class, we ensemble detection results from multiple paths by integrating random subspace sampling and a voting mechanism. Compared with state-of-the-art methods, our experimental results suggest that our method not only outperforms them, but it is also suitable for the detection of a broad range of anomaly types with high accuracy.

Monotonic Learning in the PAC Framework: A New Perspective

Monotone learning refers to learning processes in which expected performance consistently improves as more training data is introduced. Non-monotone behavior of machine learning has been the topic of a series of recent works, with various proposals that ensure monotonicity by applying transformations or wrappers on learning algorithms. In this work, from a different perspective, we tackle the topic of monotone learning within the framework of Probably Approximately Correct (PAC) learning theory. Following the mechanism that estimates sample complexity of a PAC-learnable problem, we derive a performance lower bound for that problem, and prove the monotonicity of that bound as the sample sizes increase. By calculating the lower bound distribution, we are able to prove that given a PAC-learnable problem with a hypothesis space that is either of finite size or of finite VC dimension, any learning algorithm based on Empirical Risk Minimization (ERM) is monotone if training samples are independent and identically distributed (i.i.d.). We further carry out an experiment on two concrete machine learning problems, one of which has a finite hypothesis set, and the other of finite VC dimension, and compared the experimental data for the empirical risk distributions with the estimated theoretical bound. The results of the comparison have confirmed the monotonicity of learning for the two PAC-learnable problems.

Memory Efficient Matting with Adaptive Token Routing

Transformer-based models have recently achieved outstanding performance in image matting. However, their application to high-resolution images remains challenging due to the quadratic complexity of global self-attention. To address this issue, we propose MEMatte, a \textbf{m}emory-\textbf{e}fficient \textbf{m}atting framework for processing high-resolution images. MEMatte incorporates a router before each global attention block, directing informative tokens to the global attention while routing other tokens to a Lightweight Token Refinement Module (LTRM). Specifically, the router employs a local-global strategy to predict the routing probability of each token, and the LTRM utilizes efficient modules to simulate global attention. Additionally, we introduce a Batch-constrained Adaptive Token Routing (BATR) mechanism, which allows each router to dynamically route tokens based on image content and the stages of attention block in the network. Furthermore, we construct an ultra high-resolution image matting dataset, UHR-395, comprising 35,500 training images and 1,000 test images, with an average resolution of $4872\times6017$. This dataset is created by compositing 395 different alpha mattes across 11 categories onto various backgrounds, all with high-quality manual annotation. Extensive experiments demonstrate that MEMatte outperforms existing methods on both high-resolution and real-world datasets, significantly reducing memory usage by approximately 88% and latency by 50% on the Composition-1K benchmark. Our code is available at https://github.com/linyiheng123/MEMatte.

Comparisons Are All You Need for Optimizing Smooth Functions

When optimizing machine learning models, there are various scenarios where gradient computations are challenging or even infeasible. Furthermore, in reinforcement learning (RL), preference-based RL that only compares between options has wide applications, including reinforcement learning with human feedback in large language models. In this paper, we systematically study optimization of a smooth function $f\colon\mathbb{R}^n\to\mathbb{R}$ only assuming an oracle that compares function values at two points and tells which is larger. When $f$ is convex, we give two algorithms using $\tilde{O}(n/\epsilon)$ and $\tilde{O}(n^{2})$ comparison queries to find an $\epsilon$-optimal solution, respectively. When $f$ is nonconvex, our algorithm uses $\tilde{O}(n/\epsilon^2)$ comparison queries to find an $\epsilon$-approximate stationary point. All these results match the best-known zeroth-order algorithms with function evaluation queries in $n$ dependence, thus suggest that \emph{comparisons are all you need for optimizing smooth functions using derivative-free methods}. In addition, we also give an algorithm for escaping saddle points and reaching an $\epsilon$-second order stationary point of a nonconvex $f$, using $\tilde{O}(n^{1.5}/\epsilon^{2.5})$ comparison queries.

Learning Trimaps via Clicks for Image Matting

Despite significant advancements in image matting, existing models heavily depend on manually-drawn trimaps for accurate results in natural image scenarios. However, the process of obtaining trimaps is time-consuming, lacking user-friendliness and device compatibility. This reliance greatly limits the practical application of all trimap-based matting methods. To address this issue, we introduce Click2Trimap, an interactive model capable of predicting high-quality trimaps and alpha mattes with minimal user click inputs. Through analyzing real users' behavioral logic and characteristics of trimaps, we successfully propose a powerful iterative three-class training strategy and a dedicated simulation function, making Click2Trimap exhibit versatility across various scenarios. Quantitative and qualitative assessments on synthetic and real-world matting datasets demonstrate Click2Trimap's superior performance compared to all existing trimap-free matting methods. Especially, in the user study, Click2Trimap achieves high-quality trimap and matting predictions in just an average of 5 seconds per image, demonstrating its substantial practical value in real-world applications.

Beyond Recommender: An Exploratory Study of the Effects of Different AI Roles in AI-Assisted Decision Making

Artificial Intelligence (AI) is increasingly employed in various decision-making tasks, typically as a Recommender, providing recommendations that the AI deems correct. However, recent studies suggest this may diminish human analytical thinking and lead to humans' inappropriate reliance on AI, impairing the synergy in human-AI teams. In contrast, human advisors in group decision-making perform various roles, such as analyzing alternative options or criticizing decision-makers to encourage their critical thinking. This diversity of roles has not yet been empirically explored in AI assistance. In this paper, we examine three AI roles: Recommender, Analyzer, and Devil's Advocate, and evaluate their effects across two AI performance levels. Our results show each role's distinct strengths and limitations in task performance, reliance appropriateness, and user experience. Notably, the Recommender role is not always the most effective, especially if the AI performance level is low, the Analyzer role may be preferable. These insights offer valuable implications for designing AI assistants with adaptive functional roles according to different situations.

A Mask-Based Adversarial Defense Scheme

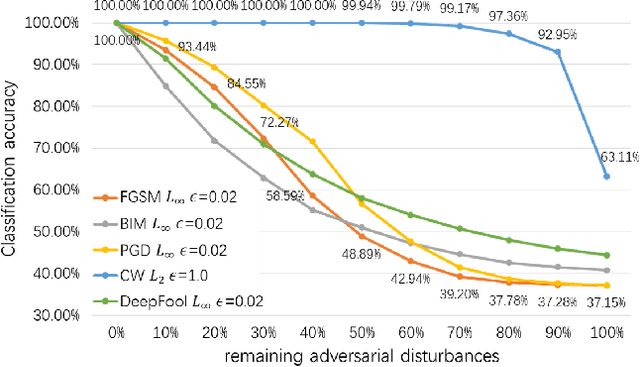
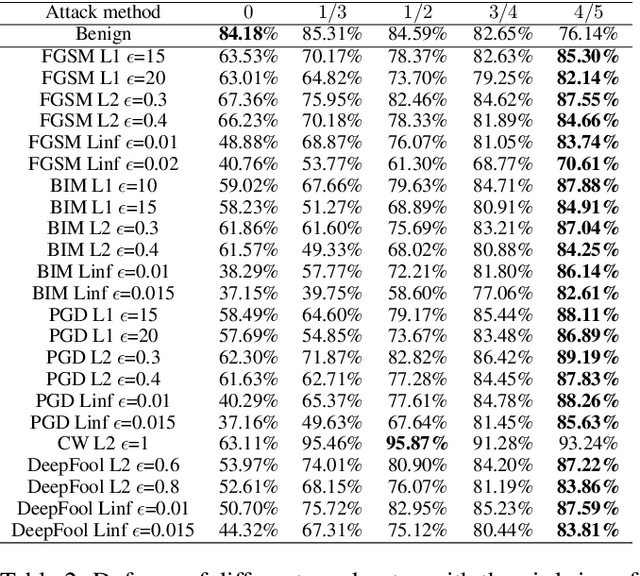
Adversarial attacks hamper the functionality and accuracy of Deep Neural Networks (DNNs) by meddling with subtle perturbations to their inputs.In this work, we propose a new Mask-based Adversarial Defense scheme (MAD) for DNNs to mitigate the negative effect from adversarial attacks. To be precise, our method promotes the robustness of a DNN by randomly masking a portion of potential adversarial images, and as a result, the %classification result output of the DNN becomes more tolerant to minor input perturbations. Compared with existing adversarial defense techniques, our method does not need any additional denoising structure, nor any change to a DNN's design. We have tested this approach on a collection of DNN models for a variety of data sets, and the experimental results confirm that the proposed method can effectively improve the defense abilities of the DNNs against all of the tested adversarial attack methods. In certain scenarios, the DNN models trained with MAD have improved classification accuracy by as much as 20% to 90% compared to the original models that are given adversarial inputs.

Escape saddle points by a simple gradient-descent based algorithm

Escaping saddle points is a central research topic in nonconvex optimization. In this paper, we propose a simple gradient-based algorithm such that for a smooth function $f\colon\mathbb{R}^n\to\mathbb{R}$, it outputs an $\epsilon$-approximate second-order stationary point in $\tilde{O}(\log n/\epsilon^{1.75})$ iterations. Compared to the previous state-of-the-art algorithms by Jin et al. with $\tilde{O}((\log n)^{4}/\epsilon^{2})$ or $\tilde{O}((\log n)^{6}/\epsilon^{1.75})$ iterations, our algorithm is polynomially better in terms of $\log n$ and matches their complexities in terms of $1/\epsilon$. For the stochastic setting, our algorithm outputs an $\epsilon$-approximate second-order stationary point in $\tilde{O}((\log n)^{2}/\epsilon^{4})$ iterations. Technically, our main contribution is an idea of implementing a robust Hessian power method using only gradients, which can find negative curvature near saddle points and achieve the polynomial speedup in $\log n$ compared to the perturbed gradient descent methods. Finally, we also perform numerical experiments that support our results.