Epidemiology-informed Graph Neural Network for Heterogeneity-aware Epidemic Forecasting

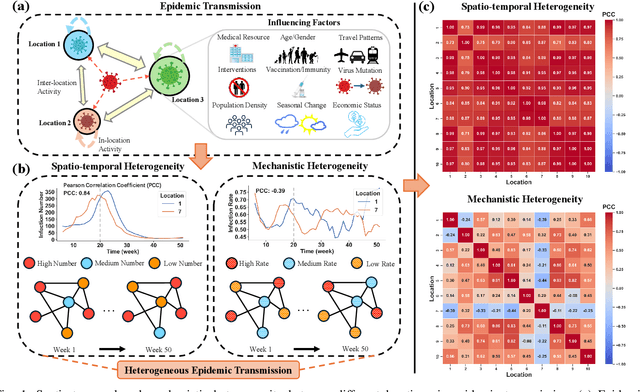
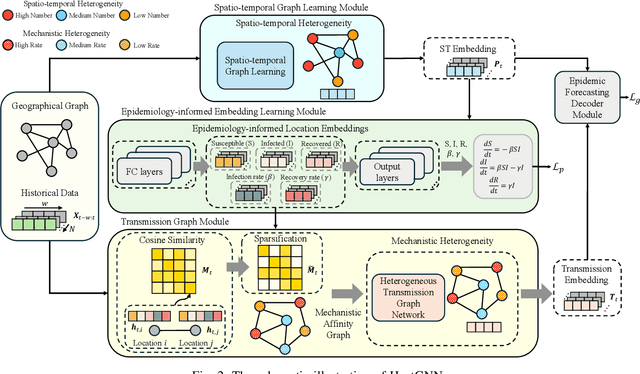
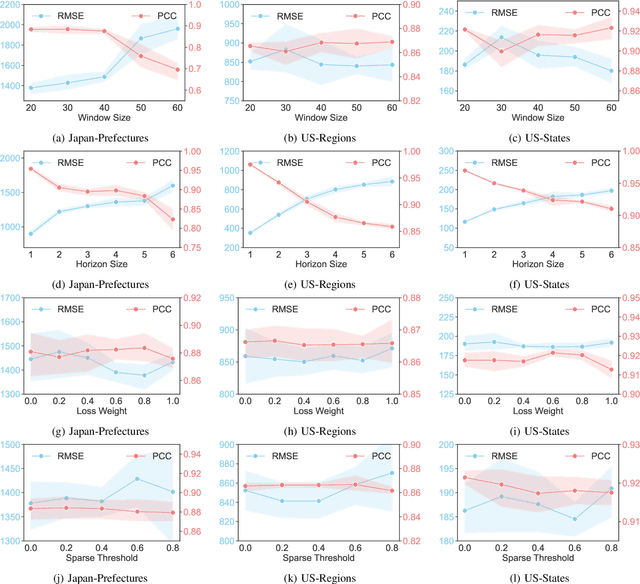
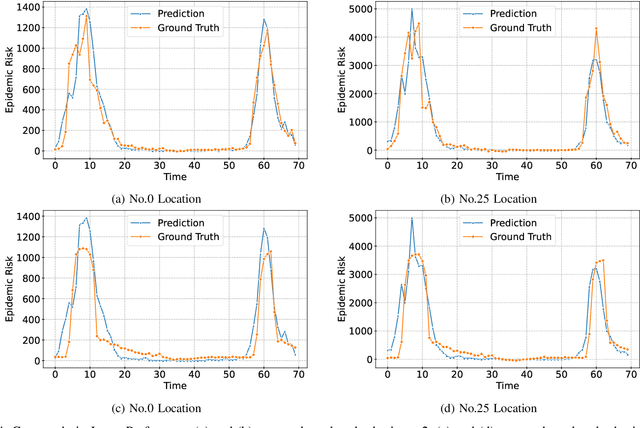
Among various spatio-temporal prediction tasks, epidemic forecasting plays a critical role in public health management. Recent studies have demonstrated the strong potential of spatio-temporal graph neural networks (STGNNs) in extracting heterogeneous spatio-temporal patterns for epidemic forecasting. However, most of these methods bear an over-simplified assumption that two locations (e.g., cities) with similar observed features in previous time steps will develop similar infection numbers in the future. In fact, for any epidemic disease, there exists strong heterogeneity of its intrinsic evolution mechanisms across geolocation and time, which can eventually lead to diverged infection numbers in two ``similar'' locations. However, such mechanistic heterogeneity is non-trivial to be captured due to the existence of numerous influencing factors like medical resource accessibility, virus mutations, mobility patterns, etc., most of which are spatio-temporal yet unreachable or even unobservable. To address this challenge, we propose a Heterogeneous Epidemic-Aware Transmission Graph Neural Network (HeatGNN), a novel epidemic forecasting framework. By binding the epidemiology mechanistic model into a GNN, HeatGNN learns epidemiology-informed location embeddings of different locations that reflect their own transmission mechanisms over time. With the time-varying mechanistic affinity graphs computed with the epidemiology-informed location embeddings, a heterogeneous transmission graph network is designed to encode the mechanistic heterogeneity among locations, providing additional predictive signals to facilitate accurate forecasting. Experiments on three benchmark datasets have revealed that HeatGNN outperforms various strong baselines. Moreover, our efficiency analysis verifies the real-world practicality of HeatGNN on datasets of different sizes.

A quantum-classical performance separation in nonconvex optimization

In this paper, we identify a family of nonconvex continuous optimization instances, each $d$-dimensional instance with $2^d$ local minima, to demonstrate a quantum-classical performance separation. Specifically, we prove that the recently proposed Quantum Hamiltonian Descent (QHD) algorithm [Leng et al., arXiv:2303.01471] is able to solve any $d$-dimensional instance from this family using $\widetilde{\mathcal{O}}(d^3)$ quantum queries to the function value and $\widetilde{\mathcal{O}}(d^4)$ additional 1-qubit and 2-qubit elementary quantum gates. On the other side, a comprehensive empirical study suggests that representative state-of-the-art classical optimization algorithms/solvers (including Gurobi) would require a super-polynomial time to solve such optimization instances.