Embrace rejection: Kernel matrix approximation by accelerated randomly pivoted Cholesky

Randomly pivoted Cholesky (RPCholesky) is an algorithm for constructing a low-rank approximation of a positive-semidefinite matrix using a small number of columns. This paper develops an accelerated version of RPCholesky that employs block matrix computations and rejection sampling to efficiently simulate the execution of the original algorithm. For the task of approximating a kernel matrix, the accelerated algorithm can run over $40\times$ faster. The paper contains implementation details, theoretical guarantees, experiments on benchmark data sets, and an application to computational chemistry.

The ESPRIT algorithm under high noise: Optimal error scaling and noisy super-resolution

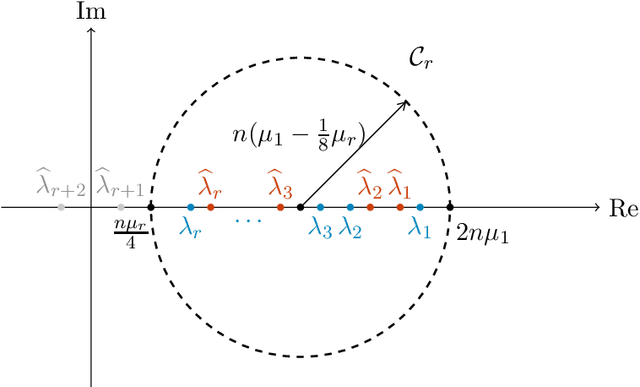
Subspace-based signal processing techniques, such as the Estimation of Signal Parameters via Rotational Invariant Techniques (ESPRIT) algorithm, are popular methods for spectral estimation. These algorithms can achieve the so-called super-resolution scaling under low noise conditions, surpassing the well-known Nyquist limit. However, the performance of these algorithms under high-noise conditions is not as well understood. Existing state-of-the-art analysis indicates that ESPRIT and related algorithms can be resilient even for signals where each observation is corrupted by statistically independent, mean-zero noise of size $\mathcal{O}(1)$, but these analyses only show that the error $\epsilon$ decays at a slow rate $\epsilon=\mathcal{\tilde{O}}(n^{-1/2})$ with respect to the cutoff frequency $n$. In this work, we prove that under certain assumptions of bias and high noise, the ESPRIT algorithm can attain a significantly improved error scaling $\epsilon = \mathcal{\tilde{O}}(n^{-3/2})$, exhibiting noisy super-resolution scaling beyond the Nyquist limit. We further establish a theoretical lower bound and show that this scaling is optimal. Our analysis introduces novel matrix perturbation results, which could be of independent interest.

Kernel Quadrature with Randomly Pivoted Cholesky

This paper presents new quadrature rules for functions in a reproducing kernel Hilbert space using nodes drawn by a sampling algorithm known as randomly pivoted Cholesky. The resulting computational procedure compares favorably to previous kernel quadrature methods, which either achieve low accuracy or require solving a computationally challenging sampling problem. Theoretical and numerical results show that randomly pivoted Cholesky is fast and achieves comparable quadrature error rates to more computationally expensive quadrature schemes based on continuous volume sampling, thinning, and recombination. Randomly pivoted Cholesky is easily adapted to complicated geometries with arbitrary kernels, unlocking new potential for kernel quadrature.

Robust, randomized preconditioning for kernel ridge regression

This paper introduces two randomized preconditioning techniques for robustly solving kernel ridge regression (KRR) problems with a medium to large number of data points ($10^4 \leq N \leq 10^7$). The first method, RPCholesky preconditioning, is capable of accurately solving the full-data KRR problem in $O(N^2)$ arithmetic operations, assuming sufficiently rapid polynomial decay of the kernel matrix eigenvalues. The second method, KRILL preconditioning, offers an accurate solution to a restricted version of the KRR problem involving $k \ll N$ selected data centers at a cost of $O((N + k^2) k \log k)$ operations. The proposed methods solve a broad range of KRR problems and overcome the failure modes of previous KRR preconditioners, making them ideal for practical applications.

Randomly pivoted Cholesky: Practical approximation of a kernel matrix with few entry evaluations

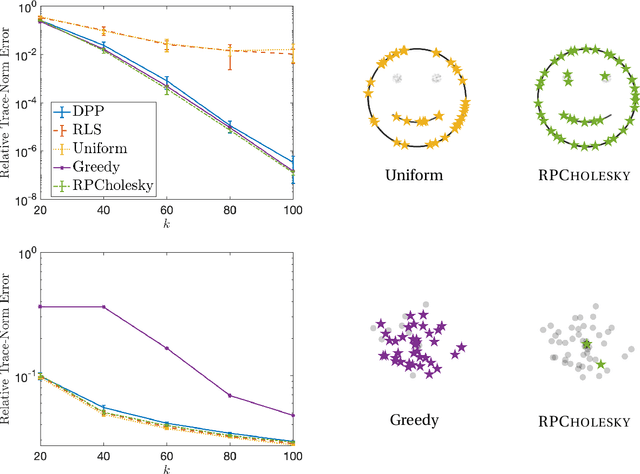
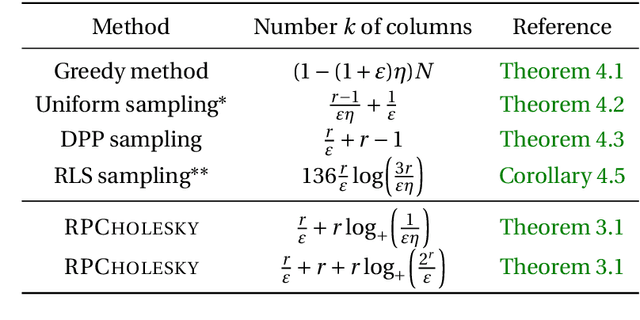
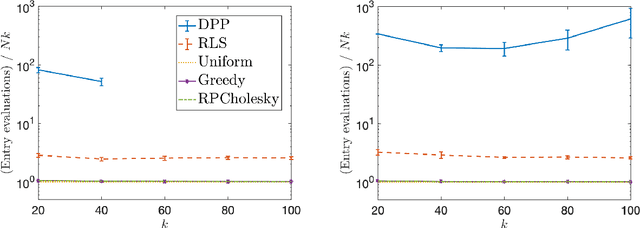
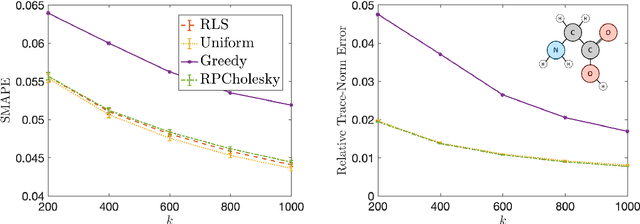
Randomly pivoted Cholesky (RPCholesky) is a natural algorithm for computing a rank-k approximation of an N x N positive semidefinite (psd) matrix. RPCholesky can be implemented with just a few lines of code. It requires only (k+1)N entry evaluations and O(k^2 N) additional arithmetic operations. This paper offers the first serious investigation of its experimental and theoretical behavior. Empirically, RPCholesky matches or improves on the performance of alternative algorithms for low-rank psd approximation. Furthermore, RPCholesky provably achieves near-optimal approximation guarantees. The simplicity, effectiveness, and robustness of this algorithm strongly support its use in scientific computing and machine learning applications.

Jackknife Variability Estimation For Randomized Matrix Computations

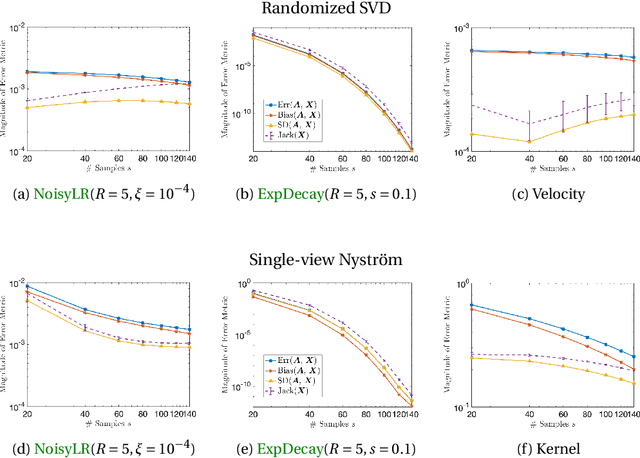
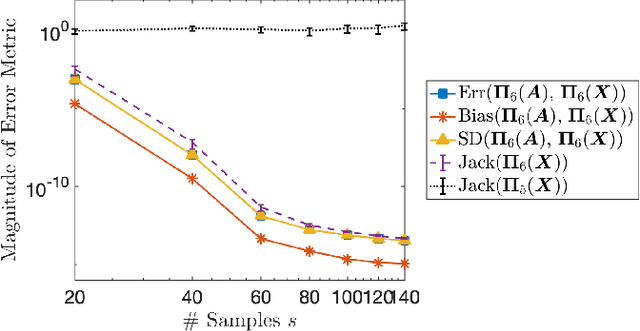
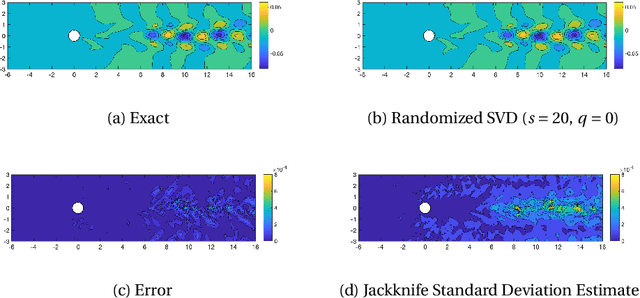
Randomized algorithms based on sketching have become a workhorse tool in low-rank matrix approximation. To use these algorithms safely in applications, they should be coupled with diagnostics to assess the quality of approximation. To meet this need, this paper proposes a jackknife resampling method to estimate the variability of the output of a randomized matrix computation. The variability estimate can recognize that a computation requires additional data or that the computation is intrinsically unstable. As examples, the paper studies jackknife estimates for two randomized low-rank matrix approximation algorithms. In each case, the operation count for the jackknife estimate is independent of the dimensions of the target matrix. In numerical experiments, the estimator accurately assesses variability and also provides an order-of-magnitude estimate of the mean-square error.