Randomly pivoted Cholesky: Practical approximation of a kernel matrix with few entry evaluations

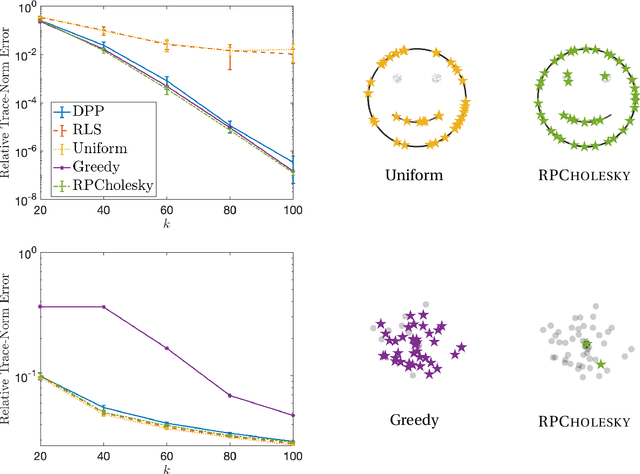
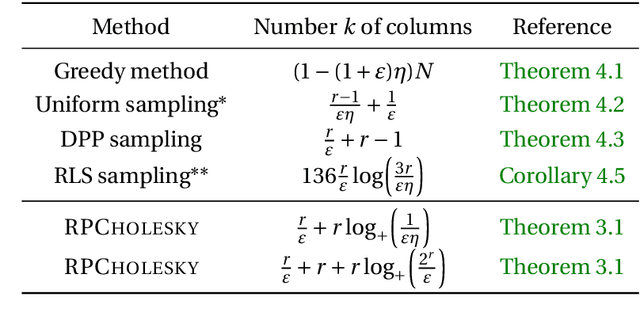
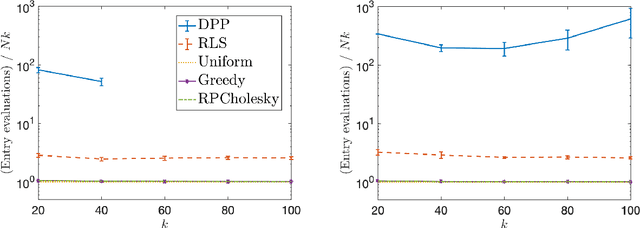
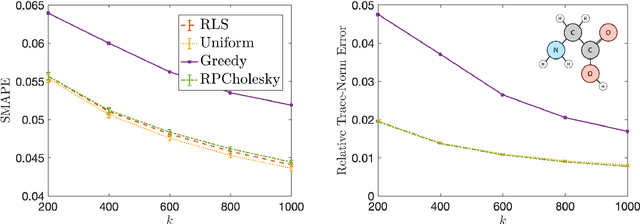
Randomly pivoted Cholesky (RPCholesky) is a natural algorithm for computing a rank-k approximation of an N x N positive semidefinite (psd) matrix. RPCholesky can be implemented with just a few lines of code. It requires only (k+1)N entry evaluations and O(k^2 N) additional arithmetic operations. This paper offers the first serious investigation of its experimental and theoretical behavior. Empirically, RPCholesky matches or improves on the performance of alternative algorithms for low-rank psd approximation. Furthermore, RPCholesky provably achieves near-optimal approximation guarantees. The simplicity, effectiveness, and robustness of this algorithm strongly support its use in scientific computing and machine learning applications.