Enhancing Physics-Informed Neural Networks Through Feature Engineering

Physics-Informed Neural Networks (PINNs) seek to solve partial differential equations (PDEs) with deep learning. Mainstream approaches that deploy fully-connected multi-layer deep learning architectures require prolonged training to achieve even moderate accuracy, while recent work on feature engineering allows higher accuracy and faster convergence. This paper introduces SAFE-NET, a Single-layered Adaptive Feature Engineering NETwork that achieves orders-of-magnitude lower errors with far fewer parameters than baseline feature engineering methods. SAFE-NET returns to basic ideas in machine learning, using Fourier features, a simplified single hidden layer network architecture, and an effective optimizer that improves the conditioning of the PINN optimization problem. Numerical results show that SAFE-NET converges faster and typically outperforms deeper networks and more complex architectures. It consistently uses fewer parameters -- on average, 65% fewer than the competing feature engineering methods -- while achieving comparable accuracy in less than 30% of the training epochs. Moreover, each SAFE-NET epoch is 95% faster than those of competing feature engineering approaches. These findings challenge the prevailing belief that modern PINNs effectively learn features in these scientific applications and highlight the efficiency gains possible through feature engineering.

SAPPHIRE: Preconditioned Stochastic Variance Reduction for Faster Large-Scale Statistical Learning

Regularized empirical risk minimization (rERM) has become important in data-intensive fields such as genomics and advertising, with stochastic gradient methods typically used to solve the largest problems. However, ill-conditioned objectives and non-smooth regularizers undermine the performance of traditional stochastic gradient methods, leading to slow convergence and significant computational costs. To address these challenges, we propose the $\texttt{SAPPHIRE}$ ($\textbf{S}$ketching-based $\textbf{A}$pproximations for $\textbf{P}$roximal $\textbf{P}$reconditioning and $\textbf{H}$essian $\textbf{I}$nexactness with Variance-$\textbf{RE}$educed Gradients) algorithm, which integrates sketch-based preconditioning to tackle ill-conditioning and uses a scaled proximal mapping to minimize the non-smooth regularizer. This stochastic variance-reduced algorithm achieves condition-number-free linear convergence to the optimum, delivering an efficient and scalable solution for ill-conditioned composite large-scale convex machine learning problems. Extensive experiments on lasso and logistic regression demonstrate that $\texttt{SAPPHIRE}$ often converges $20$ times faster than other common choices such as $\texttt{Catalyst}$, $\texttt{SAGA}$, and $\texttt{SVRG}$. This advantage persists even when the objective is non-convex or the preconditioner is infrequently updated, highlighting its robust and practical effectiveness.

CRONOS: Enhancing Deep Learning with Scalable GPU Accelerated Convex Neural Networks

We introduce the CRONOS algorithm for convex optimization of two-layer neural networks. CRONOS is the first algorithm capable of scaling to high-dimensional datasets such as ImageNet, which are ubiquitous in modern deep learning. This significantly improves upon prior work, which has been restricted to downsampled versions of MNIST and CIFAR-10. Taking CRONOS as a primitive, we then develop a new algorithm called CRONOS-AM, which combines CRONOS with alternating minimization, to obtain an algorithm capable of training multi-layer networks with arbitrary architectures. Our theoretical analysis proves that CRONOS converges to the global minimum of the convex reformulation under mild assumptions. In addition, we validate the efficacy of CRONOS and CRONOS-AM through extensive large-scale numerical experiments with GPU acceleration in JAX. Our results show that CRONOS-AM can obtain comparable or better validation accuracy than predominant tuned deep learning optimizers on vision and language tasks with benchmark datasets such as ImageNet and IMDb. To the best of our knowledge, CRONOS is the first algorithm which utilizes the convex reformulation to enhance performance on large-scale learning tasks.

Have ASkotch: Fast Methods for Large-scale, Memory-constrained Kernel Ridge Regression

Kernel ridge regression (KRR) is a fundamental computational tool, appearing in problems that range from computational chemistry to health analytics, with a particular interest due to its starring role in Gaussian process regression. However, it is challenging to scale KRR solvers to large datasets: with $n$ training points, a direct solver (i.e., Cholesky decomposition) uses $O(n^2)$ storage and $O(n^3)$ flops. Iterative methods for KRR, such as preconditioned conjugate gradient (PCG), avoid the cubic scaling of direct solvers and often use low-rank preconditioners; a rank $r$ preconditioner uses $O(rn)$ storage and each iteration requires $O(n^2)$ flops. To reduce the storage and iteration complexity of iterative solvers for KRR, we propose ASkotch ($\textbf{A}$ccelerated $\textbf{s}$calable $\textbf{k}$ernel $\textbf{o}$p$\textbf{t}$imization using block $\textbf{c}$oordinate descent with $\textbf{H}$essian preconditioning). For a given block size $|b| << n$, each iteration of ASkotch uses $O(r|b| + n)$ storage and $O(n|b|)$ flops, so ASkotch scales better than Cholesky decomposition and PCG. We prove that ASkotch obtains linear convergence to the optimum, with the convergence rate depending on the square roots of the $\textit{preconditioned}$ block condition numbers. Furthermore, we solve KRR problems that were considered to be impossibly large while using limited computational resources: we show that ASkotch outperforms PCG methods with respect to generalization error on large-scale KRR (up to $n = 10^8$) and KRR classification tasks (up to $n = 10^7$) while running each of our experiments on $\textit{a single 12 GB Titan V GPU}$. Our work opens up the possibility of as-yet-unimagined applications of KRR across a wide range of disciplines.

Challenges in Training PINNs: A Loss Landscape Perspective

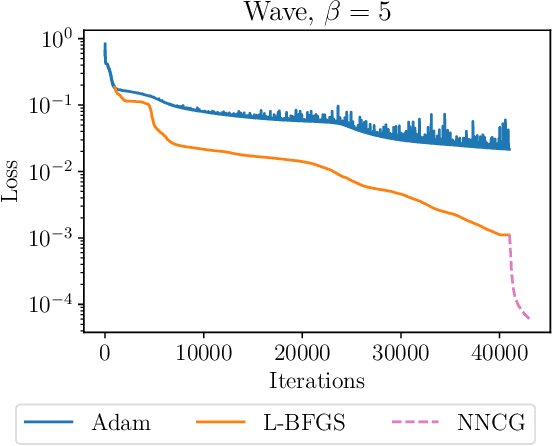
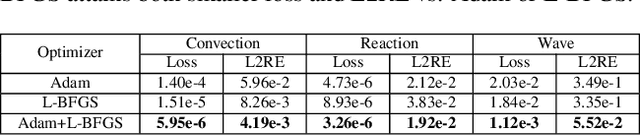
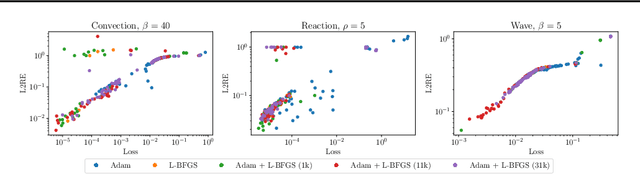
This paper explores challenges in training Physics-Informed Neural Networks (PINNs), emphasizing the role of the loss landscape in the training process. We examine difficulties in minimizing the PINN loss function, particularly due to ill-conditioning caused by differential operators in the residual term. We compare gradient-based optimizers Adam, L-BFGS, and their combination Adam+L-BFGS, showing the superiority of Adam+L-BFGS, and introduce a novel second-order optimizer, NysNewton-CG (NNCG), which significantly improves PINN performance. Theoretically, our work elucidates the connection between ill-conditioned differential operators and ill-conditioning in the PINN loss and shows the benefits of combining first- and second-order optimization methods. Our work presents valuable insights and more powerful optimization strategies for training PINNs, which could improve the utility of PINNs for solving difficult partial differential equations.

PROMISE: Preconditioned Stochastic Optimization Methods by Incorporating Scalable Curvature Estimates

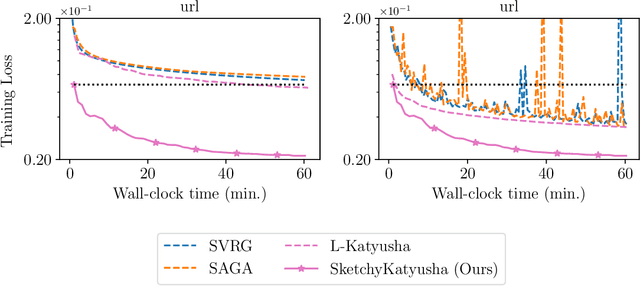
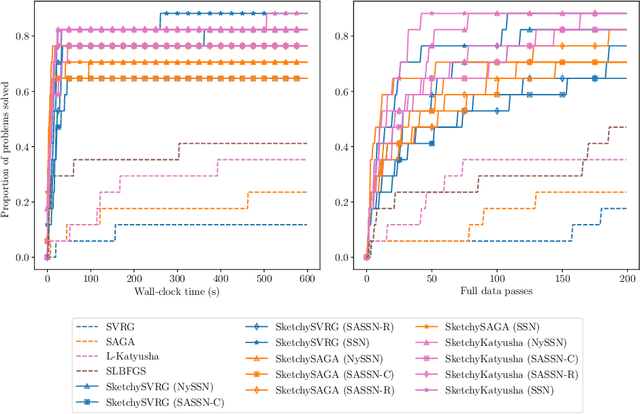
This paper introduces PROMISE ($\textbf{Pr}$econditioned Stochastic $\textbf{O}$ptimization $\textbf{M}$ethods by $\textbf{I}$ncorporating $\textbf{S}$calable Curvature $\textbf{E}$stimates), a suite of sketching-based preconditioned stochastic gradient algorithms for solving large-scale convex optimization problems arising in machine learning. PROMISE includes preconditioned versions of SVRG, SAGA, and Katyusha; each algorithm comes with a strong theoretical analysis and effective default hyperparameter values. In contrast, traditional stochastic gradient methods require careful hyperparameter tuning to succeed, and degrade in the presence of ill-conditioning, a ubiquitous phenomenon in machine learning. Empirically, we verify the superiority of the proposed algorithms by showing that, using default hyperparameter values, they outperform or match popular tuned stochastic gradient optimizers on a test bed of $51$ ridge and logistic regression problems assembled from benchmark machine learning repositories. On the theoretical side, this paper introduces the notion of quadratic regularity in order to establish linear convergence of all proposed methods even when the preconditioner is updated infrequently. The speed of linear convergence is determined by the quadratic regularity ratio, which often provides a tighter bound on the convergence rate compared to the condition number, both in theory and in practice, and explains the fast global linear convergence of the proposed methods.

Robust, randomized preconditioning for kernel ridge regression

This paper introduces two randomized preconditioning techniques for robustly solving kernel ridge regression (KRR) problems with a medium to large number of data points ($10^4 \leq N \leq 10^7$). The first method, RPCholesky preconditioning, is capable of accurately solving the full-data KRR problem in $O(N^2)$ arithmetic operations, assuming sufficiently rapid polynomial decay of the kernel matrix eigenvalues. The second method, KRILL preconditioning, offers an accurate solution to a restricted version of the KRR problem involving $k \ll N$ selected data centers at a cost of $O((N + k^2) k \log k)$ operations. The proposed methods solve a broad range of KRR problems and overcome the failure modes of previous KRR preconditioners, making them ideal for practical applications.

SketchySGD: Reliable Stochastic Optimization via Robust Curvature Estimates

We introduce SketchySGD, a stochastic quasi-Newton method that uses sketching to approximate the curvature of the loss function. Quasi-Newton methods are among the most effective algorithms in traditional optimization, where they converge much faster than first-order methods such as SGD. However, for contemporary deep learning, quasi-Newton methods are considered inferior to first-order methods like SGD and Adam owing to higher per-iteration complexity and fragility due to inexact gradients. SketchySGD circumvents these issues by a novel combination of subsampling, randomized low-rank approximation, and dynamic regularization. In the convex case, we show SketchySGD with a fixed stepsize converges to a small ball around the optimum at a faster rate than SGD for ill-conditioned problems. In the non-convex case, SketchySGD converges linearly under two additional assumptions, interpolation and the Polyak-Lojaciewicz condition, the latter of which holds with high probability for wide neural networks. Numerical experiments on image and tabular data demonstrate the improved reliability and speed of SketchySGD for deep learning, compared to standard optimizers such as SGD and Adam and existing quasi-Newton methods.

Can we globally optimize cross-validation loss? Quasiconvexity in ridge regression

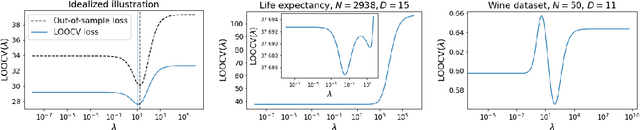
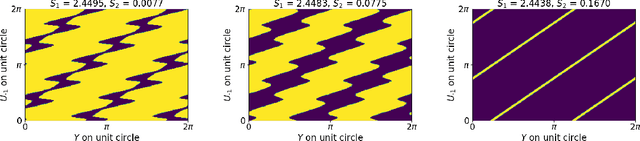
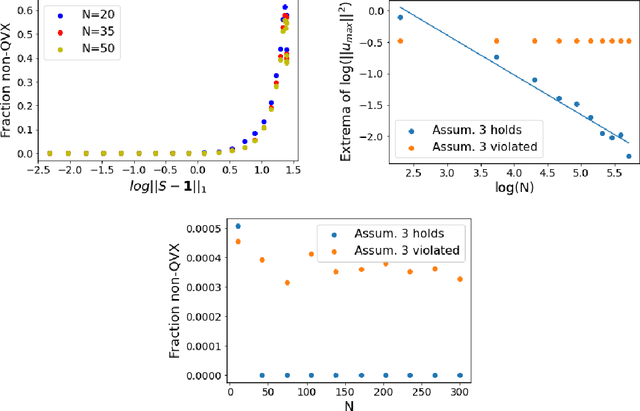
Models like LASSO and ridge regression are extensively used in practice due to their interpretability, ease of use, and strong theoretical guarantees. Cross-validation (CV) is widely used for hyperparameter tuning in these models, but do practical optimization methods minimize the true out-of-sample loss? A recent line of research promises to show that the optimum of the CV loss matches the optimum of the out-of-sample loss (possibly after simple corrections). It remains to show how tractable it is to minimize the CV loss. In the present paper, we show that, in the case of ridge regression, the CV loss may fail to be quasiconvex and thus may have multiple local optima. We can guarantee that the CV loss is quasiconvex in at least one case: when the spectrum of the covariate matrix is nearly flat and the noise in the observed responses is not too high. More generally, we show that quasiconvexity status is independent of many properties of the observed data (response norm, covariate-matrix right singular vectors and singular-value scaling) and has a complex dependence on the few that remain. We empirically confirm our theory using simulated experiments.