PROMISE: Preconditioned Stochastic Optimization Methods by Incorporating Scalable Curvature Estimates

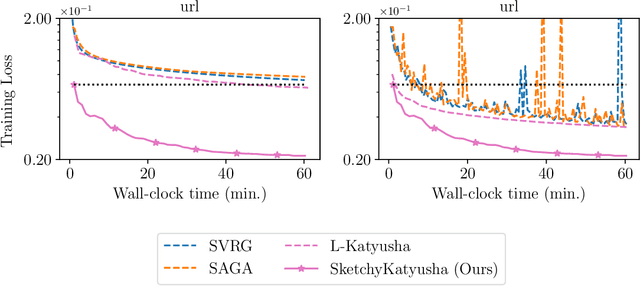
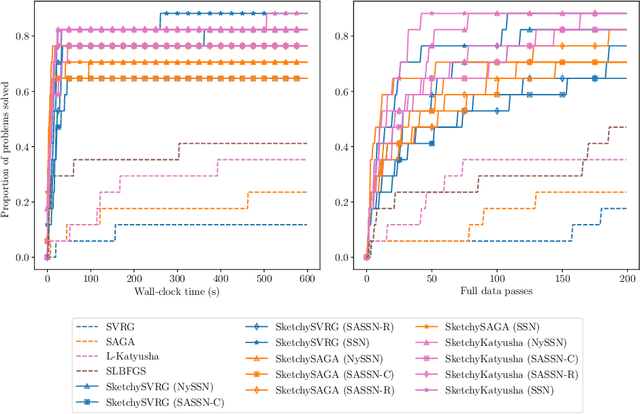
This paper introduces PROMISE ($\textbf{Pr}$econditioned Stochastic $\textbf{O}$ptimization $\textbf{M}$ethods by $\textbf{I}$ncorporating $\textbf{S}$calable Curvature $\textbf{E}$stimates), a suite of sketching-based preconditioned stochastic gradient algorithms for solving large-scale convex optimization problems arising in machine learning. PROMISE includes preconditioned versions of SVRG, SAGA, and Katyusha; each algorithm comes with a strong theoretical analysis and effective default hyperparameter values. In contrast, traditional stochastic gradient methods require careful hyperparameter tuning to succeed, and degrade in the presence of ill-conditioning, a ubiquitous phenomenon in machine learning. Empirically, we verify the superiority of the proposed algorithms by showing that, using default hyperparameter values, they outperform or match popular tuned stochastic gradient optimizers on a test bed of $51$ ridge and logistic regression problems assembled from benchmark machine learning repositories. On the theoretical side, this paper introduces the notion of quadratic regularity in order to establish linear convergence of all proposed methods even when the preconditioner is updated infrequently. The speed of linear convergence is determined by the quadratic regularity ratio, which often provides a tighter bound on the convergence rate compared to the condition number, both in theory and in practice, and explains the fast global linear convergence of the proposed methods.

SketchySGD: Reliable Stochastic Optimization via Robust Curvature Estimates

We introduce SketchySGD, a stochastic quasi-Newton method that uses sketching to approximate the curvature of the loss function. Quasi-Newton methods are among the most effective algorithms in traditional optimization, where they converge much faster than first-order methods such as SGD. However, for contemporary deep learning, quasi-Newton methods are considered inferior to first-order methods like SGD and Adam owing to higher per-iteration complexity and fragility due to inexact gradients. SketchySGD circumvents these issues by a novel combination of subsampling, randomized low-rank approximation, and dynamic regularization. In the convex case, we show SketchySGD with a fixed stepsize converges to a small ball around the optimum at a faster rate than SGD for ill-conditioned problems. In the non-convex case, SketchySGD converges linearly under two additional assumptions, interpolation and the Polyak-Lojaciewicz condition, the latter of which holds with high probability for wide neural networks. Numerical experiments on image and tabular data demonstrate the improved reliability and speed of SketchySGD for deep learning, compared to standard optimizers such as SGD and Adam and existing quasi-Newton methods.

Distributionally Robust Chance Constrained Programming with Generative Adversarial Networks

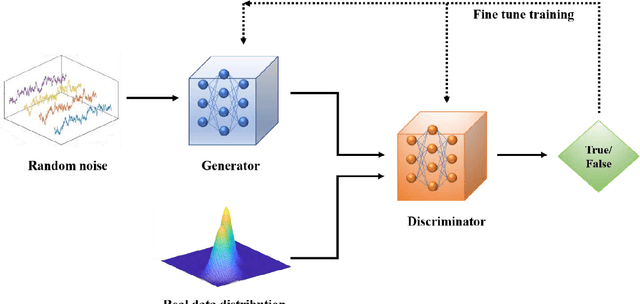
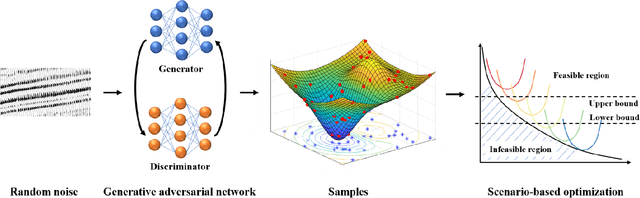
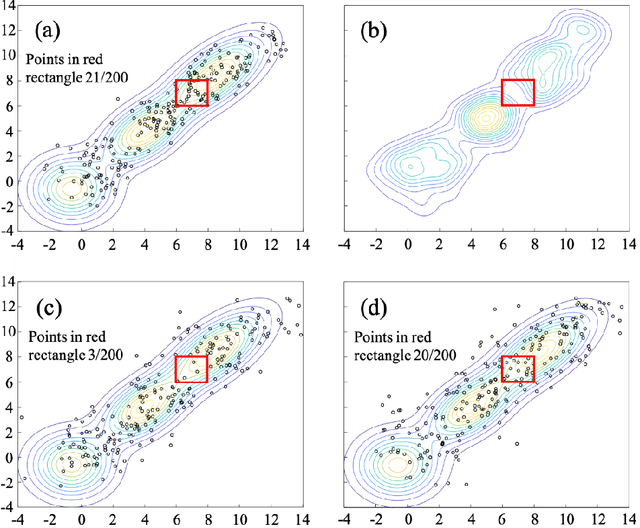
This paper presents a novel deep learning based data-driven optimization method. A novel generative adversarial network (GAN) based data-driven distributionally robust chance constrained programming framework is proposed. GAN is applied to fully extract distributional information from historical data in a nonparametric and unsupervised way without a priori approximation or assumption. Since GAN utilizes deep neural networks, complicated data distributions and modes can be learned, and it can model uncertainty efficiently and accurately. Distributionally robust chance constrained programming takes into consideration ambiguous probability distributions of uncertain parameters. To tackle the computational challenges, sample average approximation method is adopted, and the required data samples are generated by GAN in an end-to-end way through the differentiable networks. The proposed framework is then applied to supply chain optimization under demand uncertainty. The applicability of the proposed approach is illustrated through a county-level case study of a spatially explicit biofuel supply chain in Illinois.