Small Gradient Norm Regret for Online Convex Optimization

This paper introduces a new problem-dependent regret measure for online convex optimization with smooth losses. The notion, which we call the $G^\star$ regret, depends on the cumulative squared gradient norm evaluated at the decision in hindsight $\sum_{t=1}^T \|\nabla \ell(x^\star)\|^2$. We show that the $G^\star$ regret strictly refines the existing $L^\star$ (small loss) regret, and that it can be arbitrarily sharper when the losses have vanishing curvature around the hindsight decision. We establish upper and lower bounds on the $G^\star$ regret and extend our results to dynamic regret and bandit settings. As a byproduct, we refine the existing convergence analysis of stochastic optimization algorithms in the interpolation regime. Some experiments validate our theoretical findings.

Gradient Methods with Online Scaling Part I. Theoretical Foundations

This paper establishes the theoretical foundations of the online scaled gradient methods (OSGM), a framework that utilizes online learning to adapt stepsizes and provably accelerate first-order methods. OSGM quantifies the effectiveness of a stepsize by a feedback function motivated from a convergence measure and uses the feedback to adjust the stepsize through an online learning algorithm. Consequently, instantiations of OSGM achieve convergence rates that are asymptotically no worse than the optimal stepsize. OSGM yields desirable convergence guarantees on smooth convex problems, including 1) trajectory-dependent global convergence on smooth convex objectives; 2) an improved complexity result on smooth strongly convex problems, and 3) local superlinear convergence. Notably, OSGM constitutes a new family of first-order methods with non-asymptotic superlinear convergence, joining the celebrated quasi-Newton methods. Finally, OSGM explains the empirical success of the popular hypergradient-descent heuristic in optimization for machine learning.

Turbocharging Gaussian Process Inference with Approximate Sketch-and-Project

Gaussian processes (GPs) play an essential role in biostatistics, scientific machine learning, and Bayesian optimization for their ability to provide probabilistic predictions and model uncertainty. However, GP inference struggles to scale to large datasets (which are common in modern applications), since it requires the solution of a linear system whose size scales quadratically with the number of samples in the dataset. We propose an approximate, distributed, accelerated sketch-and-project algorithm ($\texttt{ADASAP}$) for solving these linear systems, which improves scalability. We use the theory of determinantal point processes to show that the posterior mean induced by sketch-and-project rapidly converges to the true posterior mean. In particular, this yields the first efficient, condition number-free algorithm for estimating the posterior mean along the top spectral basis functions, showing that our approach is principled for GP inference. $\texttt{ADASAP}$ outperforms state-of-the-art solvers based on conjugate gradient and coordinate descent across several benchmark datasets and a large-scale Bayesian optimization task. Moreover, $\texttt{ADASAP}$ scales to a dataset with $> 3 \cdot 10^8$ samples, a feat which has not been accomplished in the literature.

Understanding Fixed Predictions via Confined Regions

Machine learning models are designed to predict outcomes using features about an individual, but fail to take into account how individuals can change them. Consequently, models can assign fixed predictions that deny individuals recourse to change their outcome. This work develops a new paradigm to identify fixed predictions by finding confined regions in which all individuals receive fixed predictions. We introduce the first method, ReVer, for this task, using tools from mixed-integer quadratically constrained programming. Our approach certifies recourse for out-of-sample data, provides interpretable descriptions of confined regions, and runs in seconds on real world datasets. We conduct a comprehensive empirical study of confined regions across diverse applications. Our results highlight that existing point-wise verification methods fail to discover confined regions, while ReVer provably succeeds.

Enhancing Physics-Informed Neural Networks Through Feature Engineering

Physics-Informed Neural Networks (PINNs) seek to solve partial differential equations (PDEs) with deep learning. Mainstream approaches that deploy fully-connected multi-layer deep learning architectures require prolonged training to achieve even moderate accuracy, while recent work on feature engineering allows higher accuracy and faster convergence. This paper introduces SAFE-NET, a Single-layered Adaptive Feature Engineering NETwork that achieves orders-of-magnitude lower errors with far fewer parameters than baseline feature engineering methods. SAFE-NET returns to basic ideas in machine learning, using Fourier features, a simplified single hidden layer network architecture, and an effective optimizer that improves the conditioning of the PINN optimization problem. Numerical results show that SAFE-NET converges faster and typically outperforms deeper networks and more complex architectures. It consistently uses fewer parameters -- on average, 65% fewer than the competing feature engineering methods -- while achieving comparable accuracy in less than 30% of the training epochs. Moreover, each SAFE-NET epoch is 95% faster than those of competing feature engineering approaches. These findings challenge the prevailing belief that modern PINNs effectively learn features in these scientific applications and highlight the efficiency gains possible through feature engineering.

SAPPHIRE: Preconditioned Stochastic Variance Reduction for Faster Large-Scale Statistical Learning

Regularized empirical risk minimization (rERM) has become important in data-intensive fields such as genomics and advertising, with stochastic gradient methods typically used to solve the largest problems. However, ill-conditioned objectives and non-smooth regularizers undermine the performance of traditional stochastic gradient methods, leading to slow convergence and significant computational costs. To address these challenges, we propose the $\texttt{SAPPHIRE}$ ($\textbf{S}$ketching-based $\textbf{A}$pproximations for $\textbf{P}$roximal $\textbf{P}$reconditioning and $\textbf{H}$essian $\textbf{I}$nexactness with Variance-$\textbf{RE}$educed Gradients) algorithm, which integrates sketch-based preconditioning to tackle ill-conditioning and uses a scaled proximal mapping to minimize the non-smooth regularizer. This stochastic variance-reduced algorithm achieves condition-number-free linear convergence to the optimum, delivering an efficient and scalable solution for ill-conditioned composite large-scale convex machine learning problems. Extensive experiments on lasso and logistic regression demonstrate that $\texttt{SAPPHIRE}$ often converges $20$ times faster than other common choices such as $\texttt{Catalyst}$, $\texttt{SAGA}$, and $\texttt{SVRG}$. This advantage persists even when the objective is non-convex or the preconditioner is infrequently updated, highlighting its robust and practical effectiveness.

LLMs for Cold-Start Cutting Plane Separator Configuration

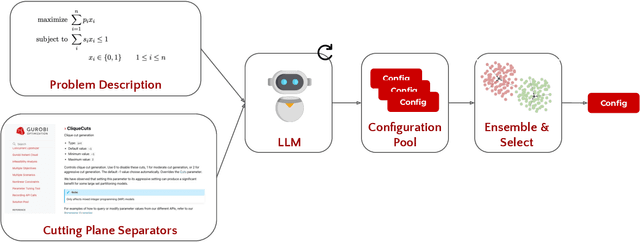
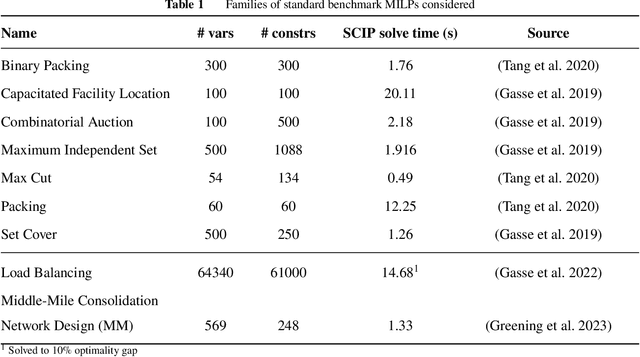
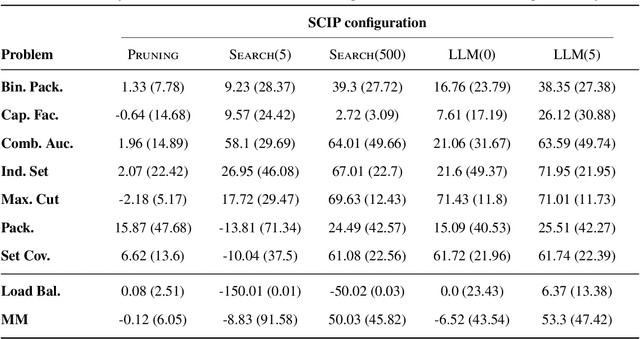
Mixed integer linear programming (MILP) solvers ship with a staggering number of parameters that are challenging to select a priori for all but expert optimization users, but can have an outsized impact on the performance of the MILP solver. Existing machine learning (ML) approaches to configure solvers require training ML models by solving thousands of related MILP instances, generalize poorly to new problem sizes, and often require implementing complex ML pipelines and custom solver interfaces that can be difficult to integrate into existing optimization workflows. In this paper, we introduce a new LLM-based framework to configure which cutting plane separators to use for a given MILP problem with little to no training data based on characteristics of the instance, such as a natural language description of the problem and the associated LaTeX formulation. We augment these LLMs with descriptions of cutting plane separators available in a given solver, grounded by summarizing the existing research literature on separators. While individual solver configurations have a large variance in performance, we present a novel ensembling strategy that clusters and aggregates configurations to create a small portfolio of high-performing configurations. Our LLM-based methodology requires no custom solver interface, can find a high-performing configuration by solving only a small number of MILPs, and can generate the configuration with simple API calls that run in under a second. Numerical results show our approach is competitive with existing configuration approaches on a suite of classic combinatorial optimization problems and real-world datasets with only a fraction of the training data and computation time.

DNAMite: Interpretable Calibrated Survival Analysis with Discretized Additive Models

Survival analysis is a classic problem in statistics with important applications in healthcare. Most machine learning models for survival analysis are black-box models, limiting their use in healthcare settings where interpretability is paramount. More recently, glass-box machine learning models have been introduced for survival analysis, with both strong predictive performance and interpretability. Still, several gaps remain, as no prior glass-box survival model can produce calibrated shape functions with enough flexibility to capture the complex patterns often found in real data. To fill this gap, we introduce a new glass-box machine learning model for survival analysis called DNAMite. DNAMite uses feature discretization and kernel smoothing in its embedding module, making it possible to learn shape functions with a flexible balance of smoothness and jaggedness. Further, DNAMite produces calibrated shape functions that can be directly interpreted as contributions to the cumulative incidence function. Our experiments show that DNAMite generates shape functions closer to true shape functions on synthetic data, while making predictions with comparable predictive performance and better calibration than previous glass-box and black-box models.

Gradient Methods with Online Scaling

We introduce a framework to accelerate the convergence of gradient-based methods with online learning. The framework learns to scale the gradient at each iteration through an online learning algorithm and provably accelerates gradient-based methods asymptotically. In contrast with previous literature, where convergence is established based on worst-case analysis, our framework provides a strong convergence guarantee with respect to the optimal scaling matrix for the iteration trajectory. For smooth strongly convex optimization, our results provide an $O(\kappa^\star \log(1/\varepsilon)$) complexity result, where $\kappa^\star$ is the condition number achievable by the optimal preconditioner, improving on the previous $O(\sqrt{n}\kappa^\star \log(1/\varepsilon))$ result. In particular, a variant of our method achieves superlinear convergence on convex quadratics. For smooth convex optimization, we show for the first time that the widely-used hypergradient descent heuristic improves on the convergence of gradient descent.

AI-Driven Review Systems: Evaluating LLMs in Scalable and Bias-Aware Academic Reviews

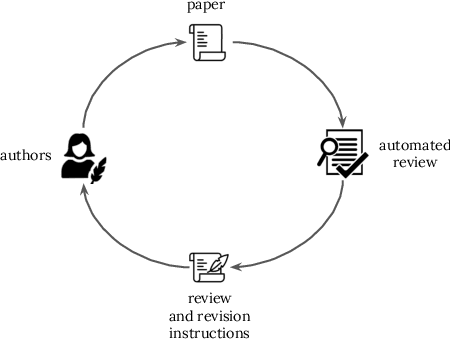
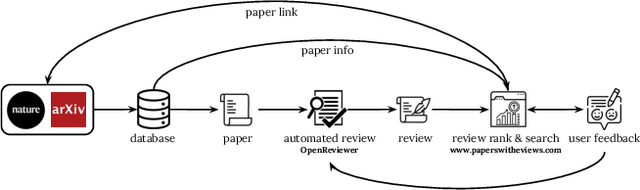
Automatic reviewing helps handle a large volume of papers, provides early feedback and quality control, reduces bias, and allows the analysis of trends. We evaluate the alignment of automatic paper reviews with human reviews using an arena of human preferences by pairwise comparisons. Gathering human preference may be time-consuming; therefore, we also use an LLM to automatically evaluate reviews to increase sample efficiency while reducing bias. In addition to evaluating human and LLM preferences among LLM reviews, we fine-tune an LLM to predict human preferences, predicting which reviews humans will prefer in a head-to-head battle between LLMs. We artificially introduce errors into papers and analyze the LLM's responses to identify limitations, use adaptive review questions, meta prompting, role-playing, integrate visual and textual analysis, use venue-specific reviewing materials, and predict human preferences, improving upon the limitations of the traditional review processes. We make the reviews of publicly available arXiv and open-access Nature journal papers available online, along with a free service which helps authors review and revise their research papers and improve their quality. This work develops proof-of-concept LLM reviewing systems that quickly deliver consistent, high-quality reviews and evaluate their quality. We mitigate the risks of misuse, inflated review scores, overconfident ratings, and skewed score distributions by augmenting the LLM with multiple documents, including the review form, reviewer guide, code of ethics and conduct, area chair guidelines, and previous year statistics, by finding which errors and shortcomings of the paper may be detected by automated reviews, and evaluating pairwise reviewer preferences. This work identifies and addresses the limitations of using LLMs as reviewers and evaluators and enhances the quality of the reviewing process.