AI-Driven Review Systems: Evaluating LLMs in Scalable and Bias-Aware Academic Reviews

Automatic reviewing helps handle a large volume of papers, provides early feedback and quality control, reduces bias, and allows the analysis of trends. We evaluate the alignment of automatic paper reviews with human reviews using an arena of human preferences by pairwise comparisons. Gathering human preference may be time-consuming; therefore, we also use an LLM to automatically evaluate reviews to increase sample efficiency while reducing bias. In addition to evaluating human and LLM preferences among LLM reviews, we fine-tune an LLM to predict human preferences, predicting which reviews humans will prefer in a head-to-head battle between LLMs. We artificially introduce errors into papers and analyze the LLM's responses to identify limitations, use adaptive review questions, meta prompting, role-playing, integrate visual and textual analysis, use venue-specific reviewing materials, and predict human preferences, improving upon the limitations of the traditional review processes. We make the reviews of publicly available arXiv and open-access Nature journal papers available online, along with a free service which helps authors review and revise their research papers and improve their quality. This work develops proof-of-concept LLM reviewing systems that quickly deliver consistent, high-quality reviews and evaluate their quality. We mitigate the risks of misuse, inflated review scores, overconfident ratings, and skewed score distributions by augmenting the LLM with multiple documents, including the review form, reviewer guide, code of ethics and conduct, area chair guidelines, and previous year statistics, by finding which errors and shortcomings of the paper may be detected by automated reviews, and evaluating pairwise reviewer preferences. This work identifies and addresses the limitations of using LLMs as reviewers and evaluators and enhances the quality of the reviewing process.

Identifying Exoplanets with Deep Learning. V. Improved Light Curve Classification for TESS Full Frame Image Observations

The TESS mission produces a large amount of time series data, only a small fraction of which contain detectable exoplanetary transit signals. Deep learning techniques such as neural networks have proved effective at differentiating promising astrophysical eclipsing candidates from other phenomena such as stellar variability and systematic instrumental effects in an efficient, unbiased and sustainable manner. This paper presents a high quality dataset containing light curves from the Primary Mission and 1st Extended Mission full frame images and periodic signals detected via Box Least Squares (Kov\'acs et al. 2002; Hartman 2012). The dataset was curated using a thorough manual review process then used to train a neural network called Astronet-Triage-v2. On our test set, for transiting/eclipsing events we achieve a 99.6% recall (true positives over all data with positive labels) at a precision of 75.7% (true positives over all predicted positives). Since 90% of our training data is from the Primary Mission, we also test our ability to generalize on held-out 1st Extended Mission data. Here, we find an area under the precision-recall curve of 0.965, a 4% improvement over Astronet-Triage (Yu et al. 2019). On the TESS Object of Interest (TOI) Catalog through April 2022, a shortlist of planets and planet candidates, Astronet-Triage-v2 is able to recover 3577 out of 4140 TOIs, while Astronet-Triage only recovers 3349 targets at an equal level of precision. In other words, upgrading to Astronet-Triage-v2 helps save at least 200 planet candidates from being lost. The new model is currently used for planet candidate triage in the Quick-Look Pipeline (Huang et al. 2020a,b; Kunimoto et al. 2021).

A Neural Network Solves and Generates Mathematics Problems by Program Synthesis: Calculus, Differential Equations, Linear Algebra, and More

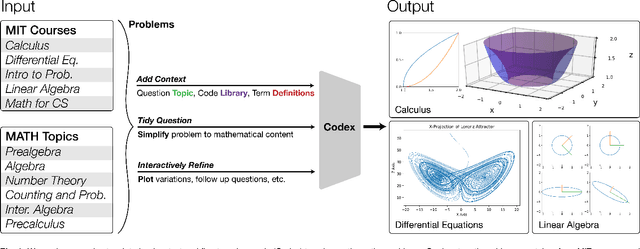
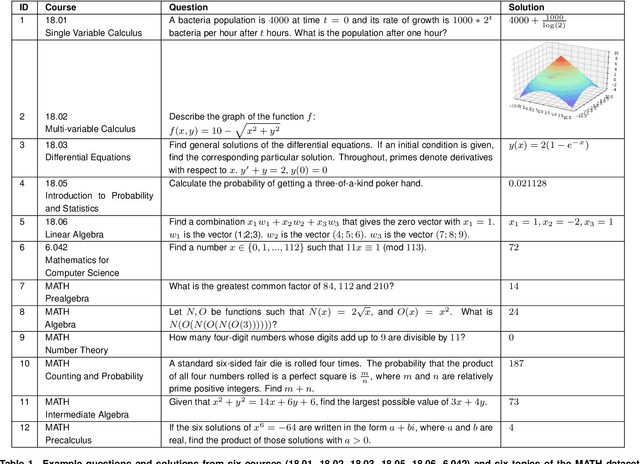
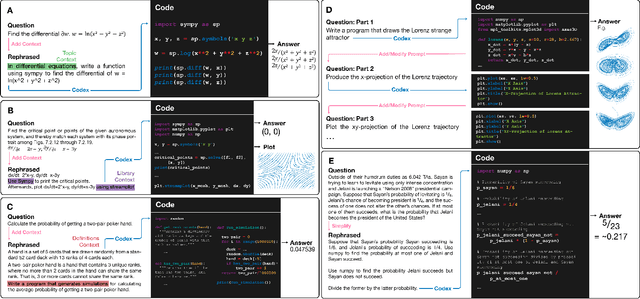
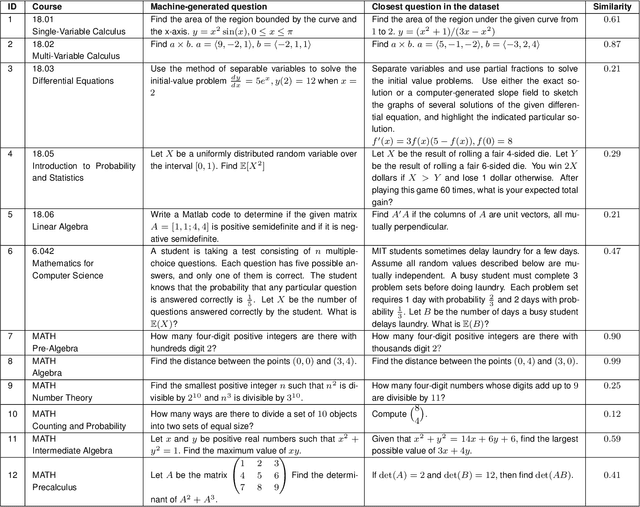
We demonstrate that a neural network pre-trained on text and fine-tuned on code solves Mathematics problems by program synthesis. We turn questions into programming tasks, automatically generate programs, and then execute them, perfectly solving university-level problems from MIT's large Mathematics courses (Single Variable Calculus 18.01, Multivariable Calculus 18.02, Differential Equations 18.03, Introduction to Probability and Statistics 18.05, Linear Algebra 18.06, and Mathematics for Computer Science 6.042), Columbia University's COMS3251 Computational Linear Algebra course, as well as questions from a MATH dataset (on Prealgebra, Algebra, Counting and Probability, Number Theory, and Precalculus), the latest benchmark of advanced mathematics problems specifically designed to assess mathematical reasoning. We explore prompt generation methods that enable Transformers to generate question solving programs for these subjects, including solutions with plots. We generate correct answers for a random sample of questions in each topic. We quantify the gap between the original and transformed questions and perform a survey to evaluate the quality and difficulty of generated questions. This is the first work to automatically solve, grade, and generate university-level Mathematics course questions at scale. This represents a milestone for higher education.