From Local to Global: A Graph RAG Approach to Query-Focused Summarization

The use of retrieval-augmented generation (RAG) to retrieve relevant information from an external knowledge source enables large language models (LLMs) to answer questions over private and/or previously unseen document collections. However, RAG fails on global questions directed at an entire text corpus, such as "What are the main themes in the dataset?", since this is inherently a query-focused summarization (QFS) task, rather than an explicit retrieval task. Prior QFS methods, meanwhile, fail to scale to the quantities of text indexed by typical RAG systems. To combine the strengths of these contrasting methods, we propose a Graph RAG approach to question answering over private text corpora that scales with both the generality of user questions and the quantity of source text to be indexed. Our approach uses an LLM to build a graph-based text index in two stages: first to derive an entity knowledge graph from the source documents, then to pregenerate community summaries for all groups of closely-related entities. Given a question, each community summary is used to generate a partial response, before all partial responses are again summarized in a final response to the user. For a class of global sensemaking questions over datasets in the 1 million token range, we show that Graph RAG leads to substantial improvements over a na\"ive RAG baseline for both the comprehensiveness and diversity of generated answers. An open-source, Python-based implementation of both global and local Graph RAG approaches is forthcoming at https://aka.ms/graphrag.

A Neural Network Solves and Generates Mathematics Problems by Program Synthesis: Calculus, Differential Equations, Linear Algebra, and More

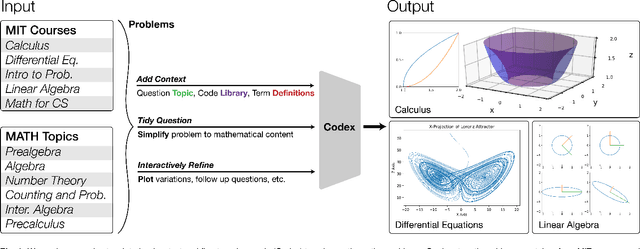
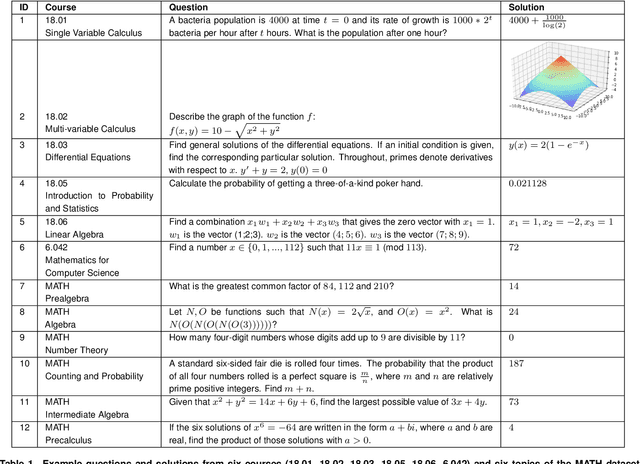
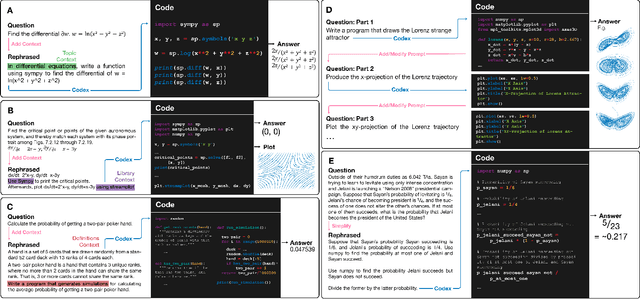
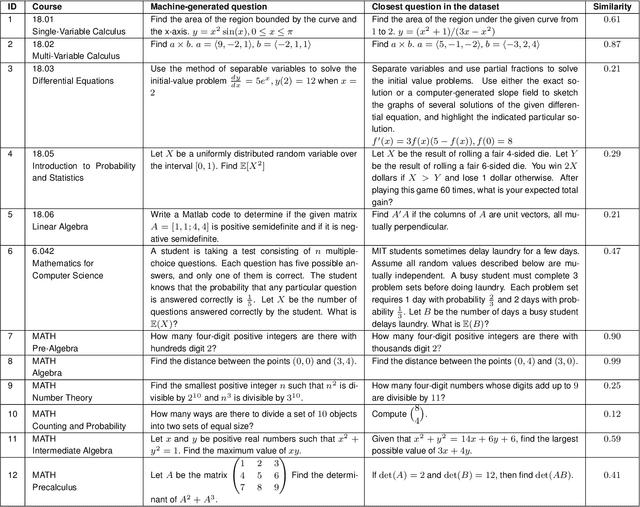
We demonstrate that a neural network pre-trained on text and fine-tuned on code solves Mathematics problems by program synthesis. We turn questions into programming tasks, automatically generate programs, and then execute them, perfectly solving university-level problems from MIT's large Mathematics courses (Single Variable Calculus 18.01, Multivariable Calculus 18.02, Differential Equations 18.03, Introduction to Probability and Statistics 18.05, Linear Algebra 18.06, and Mathematics for Computer Science 6.042), Columbia University's COMS3251 Computational Linear Algebra course, as well as questions from a MATH dataset (on Prealgebra, Algebra, Counting and Probability, Number Theory, and Precalculus), the latest benchmark of advanced mathematics problems specifically designed to assess mathematical reasoning. We explore prompt generation methods that enable Transformers to generate question solving programs for these subjects, including solutions with plots. We generate correct answers for a random sample of questions in each topic. We quantify the gap between the original and transformed questions and perform a survey to evaluate the quality and difficulty of generated questions. This is the first work to automatically solve, grade, and generate university-level Mathematics course questions at scale. This represents a milestone for higher education.

Top 3 in FG 2021 Families In the Wild Kinship Verification Challenge

Kinship verification is the task of determining whether a parent-child, sibling, or grandparent-grandchild relationship exists between two people and is important in social media applications, forensic investigations, finding missing children, and reuniting families. We demonstrate high quality kinship verification by participating in the 2021 Recognizing Families in the Wild challenge which provides the largest publicly available dataset in the field. Our approach is among the top 3 winning entries in the competition. We ensemble models written by both human experts and OpenAI Codex. We make our models and code publicly available.