Algorithms with Calibrated Machine Learning Predictions

The field of algorithms with predictions incorporates machine learning advice in the design of online algorithms to improve real-world performance. While this theoretical framework often assumes uniform reliability across all predictions, modern machine learning models can now provide instance-level uncertainty estimates. In this paper, we propose calibration as a principled and practical tool to bridge this gap, demonstrating the benefits of calibrated advice through two case studies: the ski rental and online job scheduling problems. For ski rental, we design an algorithm that achieves optimal prediction-dependent performance and prove that, in high-variance settings, calibrated advice offers more effective guidance than alternative methods for uncertainty quantification. For job scheduling, we demonstrate that using a calibrated predictor leads to significant performance improvements over existing methods. Evaluations on real-world data validate our theoretical findings, highlighting the practical impact of calibration for algorithms with predictions.

LLMs for Cold-Start Cutting Plane Separator Configuration

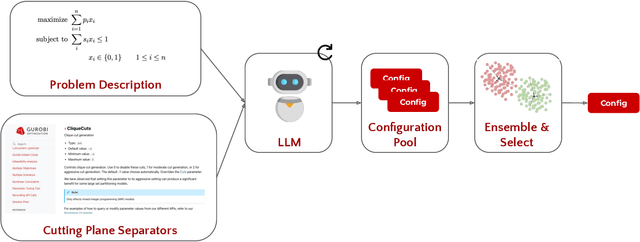
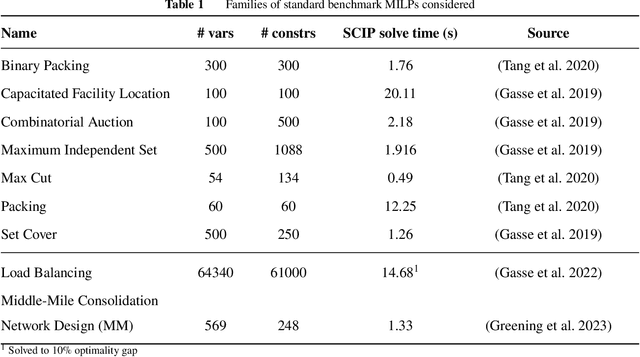
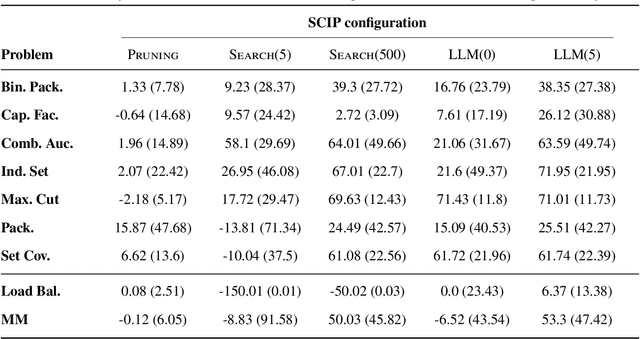
Mixed integer linear programming (MILP) solvers ship with a staggering number of parameters that are challenging to select a priori for all but expert optimization users, but can have an outsized impact on the performance of the MILP solver. Existing machine learning (ML) approaches to configure solvers require training ML models by solving thousands of related MILP instances, generalize poorly to new problem sizes, and often require implementing complex ML pipelines and custom solver interfaces that can be difficult to integrate into existing optimization workflows. In this paper, we introduce a new LLM-based framework to configure which cutting plane separators to use for a given MILP problem with little to no training data based on characteristics of the instance, such as a natural language description of the problem and the associated LaTeX formulation. We augment these LLMs with descriptions of cutting plane separators available in a given solver, grounded by summarizing the existing research literature on separators. While individual solver configurations have a large variance in performance, we present a novel ensembling strategy that clusters and aggregates configurations to create a small portfolio of high-performing configurations. Our LLM-based methodology requires no custom solver interface, can find a high-performing configuration by solving only a small number of MILPs, and can generate the configuration with simple API calls that run in under a second. Numerical results show our approach is competitive with existing configuration approaches on a suite of classic combinatorial optimization problems and real-world datasets with only a fraction of the training data and computation time.

MAGNOLIA: Matching Algorithms via GNNs for Online Value-to-go Approximation

Online Bayesian bipartite matching is a central problem in digital marketplaces and exchanges, including advertising, crowdsourcing, ridesharing, and kidney exchange. We introduce a graph neural network (GNN) approach that emulates the problem's combinatorially-complex optimal online algorithm, which selects actions (e.g., which nodes to match) by computing each action's value-to-go (VTG) -- the expected weight of the final matching if the algorithm takes that action, then acts optimally in the future. We train a GNN to estimate VTG and show empirically that this GNN returns high-weight matchings across a variety of tasks. Moreover, we identify a common family of graph distributions in spatial crowdsourcing applications, such as rideshare, under which VTG can be efficiently approximated by aggregating information within local neighborhoods in the graphs. This structure matches the local behavior of GNNs, providing theoretical justification for our approach.