Connor Lawless
Understanding Fixed Predictions via Confined Regions
Feb 22, 2025Abstract:Machine learning models are designed to predict outcomes using features about an individual, but fail to take into account how individuals can change them. Consequently, models can assign fixed predictions that deny individuals recourse to change their outcome. This work develops a new paradigm to identify fixed predictions by finding confined regions in which all individuals receive fixed predictions. We introduce the first method, ReVer, for this task, using tools from mixed-integer quadratically constrained programming. Our approach certifies recourse for out-of-sample data, provides interpretable descriptions of confined regions, and runs in seconds on real world datasets. We conduct a comprehensive empirical study of confined regions across diverse applications. Our results highlight that existing point-wise verification methods fail to discover confined regions, while ReVer provably succeeds.
EquivaMap: Leveraging LLMs for Automatic Equivalence Checking of Optimization Formulations
Feb 20, 2025



Abstract:A fundamental problem in combinatorial optimization is identifying equivalent formulations, which can lead to more efficient solution strategies and deeper insights into a problem's computational complexity. The need to automatically identify equivalence between problem formulations has grown as optimization copilots--systems that generate problem formulations from natural language descriptions--have proliferated. However, existing approaches to checking formulation equivalence lack grounding, relying on simple heuristics which are insufficient for rigorous validation. Inspired by Karp reductions, in this work we introduce quasi-Karp equivalence, a formal criterion for determining when two optimization formulations are equivalent based on the existence of a mapping between their decision variables. We propose EquivaMap, a framework that leverages large language models to automatically discover such mappings, enabling scalable and reliable equivalence verification. To evaluate our approach, we construct the first open-source dataset of equivalent optimization formulations, generated by applying transformations such as adding slack variables or valid inequalities to existing formulations. Empirically, EquivaMap significantly outperforms existing methods, achieving substantial improvements in correctly identifying formulation equivalence.
LLMs for Cold-Start Cutting Plane Separator Configuration
Dec 16, 2024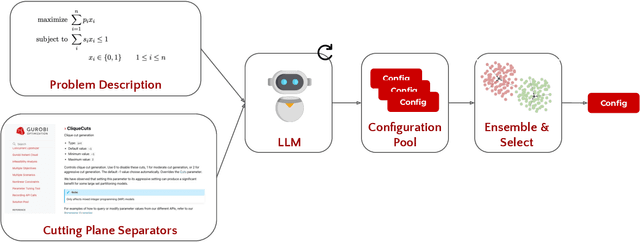
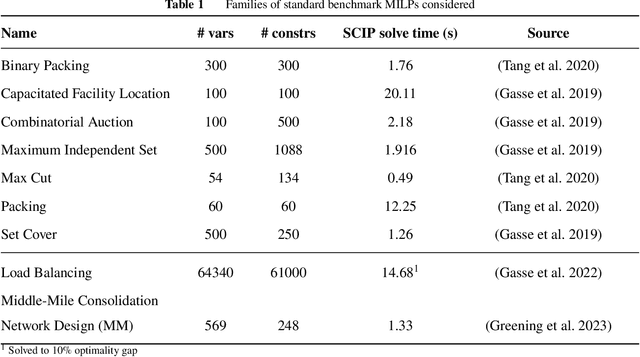

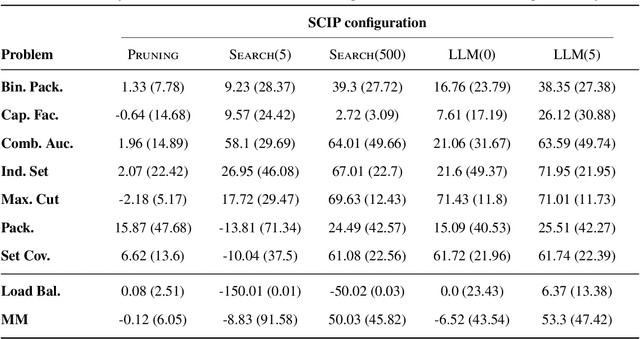
Abstract:Mixed integer linear programming (MILP) solvers ship with a staggering number of parameters that are challenging to select a priori for all but expert optimization users, but can have an outsized impact on the performance of the MILP solver. Existing machine learning (ML) approaches to configure solvers require training ML models by solving thousands of related MILP instances, generalize poorly to new problem sizes, and often require implementing complex ML pipelines and custom solver interfaces that can be difficult to integrate into existing optimization workflows. In this paper, we introduce a new LLM-based framework to configure which cutting plane separators to use for a given MILP problem with little to no training data based on characteristics of the instance, such as a natural language description of the problem and the associated LaTeX formulation. We augment these LLMs with descriptions of cutting plane separators available in a given solver, grounded by summarizing the existing research literature on separators. While individual solver configurations have a large variance in performance, we present a novel ensembling strategy that clusters and aggregates configurations to create a small portfolio of high-performing configurations. Our LLM-based methodology requires no custom solver interface, can find a high-performing configuration by solving only a small number of MILPs, and can generate the configuration with simple API calls that run in under a second. Numerical results show our approach is competitive with existing configuration approaches on a suite of classic combinatorial optimization problems and real-world datasets with only a fraction of the training data and computation time.
Fair Minimum Representation Clustering via Integer Programming
Sep 04, 2024Abstract:Clustering is an unsupervised learning task that aims to partition data into a set of clusters. In many applications, these clusters correspond to real-world constructs (e.g., electoral districts, playlists, TV channels) whose benefit can only be attained by groups when they reach a minimum level of representation (e.g., 50\% to elect their desired candidate). In this paper, we study the k-means and k-medians clustering problems with the additional constraint that each group (e.g., demographic group) must have a minimum level of representation in at least a given number of clusters. We formulate the problem through a mixed-integer optimization framework and present an alternating minimization algorithm, called MiniReL, that directly incorporates the fairness constraints. While incorporating the fairness criteria leads to an NP-Hard assignment problem within the algorithm, we provide computational approaches that make the algorithm practical even for large datasets. Numerical results show that the approach is able to create fairer clusters with practically no increase in the clustering cost across standard benchmark datasets.
Fair Minimum Representation Clustering
Feb 08, 2023Abstract:Clustering is an unsupervised learning task that aims to partition data into a set of clusters. In many applications, these clusters correspond to real-world constructs (e.g. electoral districts) whose benefit can only be attained by groups when they reach a minimum level of representation (e.g. 50\% to elect their desired candidate). This paper considers the problem of performing k-means clustering while ensuring groups (e.g. demographic groups) have that minimum level of representation in a specified number of clusters. We show that the popular $k$-means algorithm, Lloyd's algorithm, can result in unfair outcomes where certain groups lack sufficient representation past the minimum threshold in a proportional number of clusters. We formulate the problem through a mixed-integer optimization framework and present a variant of Lloyd's algorithm, called MiniReL, that directly incorporates the fairness constraints. We show that incorporating the fairness criteria leads to a NP-Hard sub-problem within Lloyd's algorithm, but we provide computational approaches that make the problem tractable for even large datasets. Numerical results show that the approach is able to create fairer clusters with practically no increase in the k-means clustering cost across standard benchmark datasets.
A Note on Task-Aware Loss via Reweighing Prediction Loss by Decision-Regret
Nov 09, 2022Abstract:In this short technical note we propose a baseline for decision-aware learning for contextual linear optimization, which solves stochastic linear optimization when cost coefficients can be predicted based on context information. We propose a decision-aware version of predict-then-optimize. We reweigh the prediction error by the decision regret incurred by an (unweighted) pilot estimator of costs to obtain a decision-aware predictor, then optimize with cost predictions from the decision-aware predictor. This method can be motivated as a finite-difference, iterate-independent approximation of the gradients of previously proposed end-to-end learning algorithms; it is also consistent with previously suggested intuition for end-to-end learning. This baseline is computationally easy to implement with readily available reweighted prediction oracles and linear optimization, and can be implemented with convex optimization so long as the prediction error minimization is convex. Empirically, we demonstrate that this approach can lead to improvements over a "predict-then-optimize" framework for settings with misspecified models, and is competitive with other end-to-end approaches. Therefore, due to its simplicity and ease of use, we suggest it as a simple baseline for end-to-end and decision-aware learning.
Cluster Explanation via Polyhedral Descriptions
Oct 17, 2022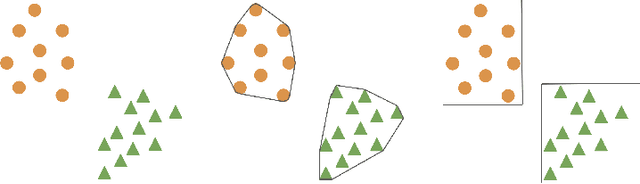
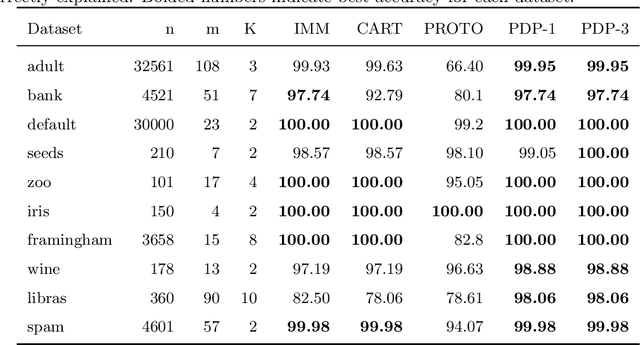
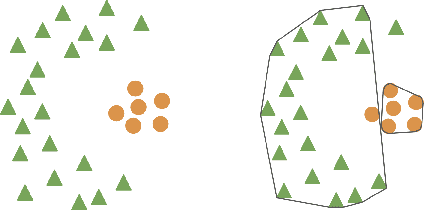
Abstract:Clustering is an unsupervised learning problem that aims to partition unlabelled data points into groups with similar features. Traditional clustering algorithms provide limited insight into the groups they find as their main focus is accuracy and not the interpretability of the group assignments. This has spurred a recent line of work on explainable machine learning for clustering. In this paper we focus on the cluster description problem where, given a dataset and its partition into clusters, the task is to explain the clusters. We introduce a new approach to explain clusters by constructing polyhedra around each cluster while minimizing either the complexity of the resulting polyhedra or the number of features used in the description. We formulate the cluster description problem as an integer program and present a column generation approach to search over an exponential number of candidate half-spaces that can be used to build the polyhedra. To deal with large datasets, we introduce a novel grouping scheme that first forms smaller groups of data points and then builds the polyhedra around the grouped data, a strategy which out-performs simply sub-sampling data. Compared to state of the art cluster description algorithms, our approach is able to achieve competitive interpretability with improved description accuracy.
Interpretable Clustering via Multi-Polytope Machines
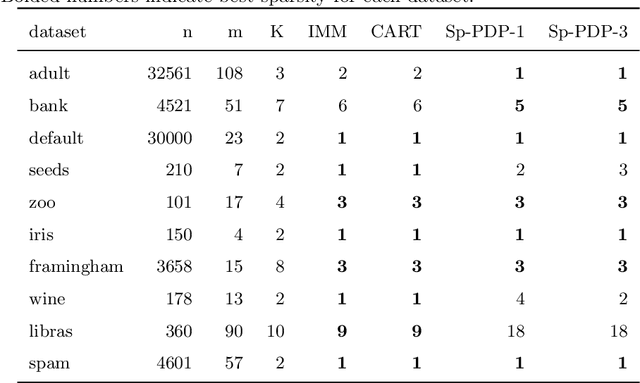
Dec 10, 2021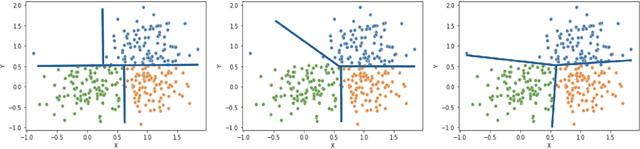
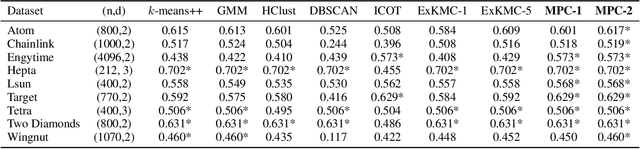


Abstract:Clustering is a popular unsupervised learning tool often used to discover groups within a larger population such as customer segments, or patient subtypes. However, despite its use as a tool for subgroup discovery and description - few state-of-the-art algorithms provide any rationale or description behind the clusters found. We propose a novel approach for interpretable clustering that both clusters data points and constructs polytopes around the discovered clusters to explain them. Our framework allows for additional constraints on the polytopes - including ensuring that the hyperplanes constructing the polytope are axis-parallel or sparse with integer coefficients. We formulate the problem of constructing clusters via polytopes as a Mixed-Integer Non-Linear Program (MINLP). To solve our formulation we propose a two phase approach where we first initialize clusters and polytopes using alternating minimization, and then use coordinate descent to boost clustering performance. We benchmark our approach on a suite of synthetic and real world clustering problems, where our algorithm outperforms state of the art interpretable and non-interpretable clustering algorithms.
Interpretable and Fair Boolean Rule Sets via Column Generation
Nov 16, 2021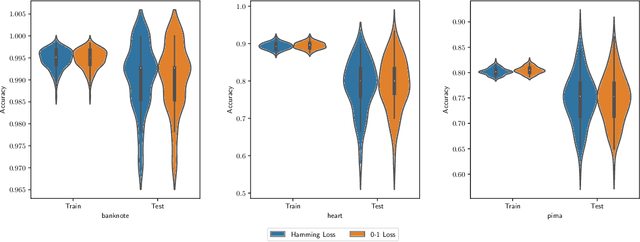
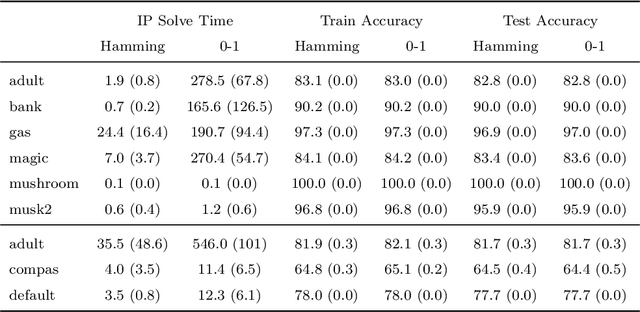
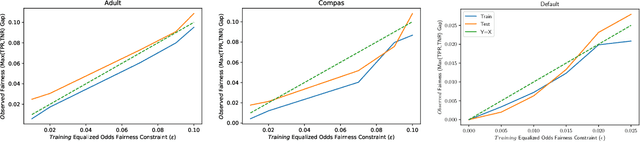
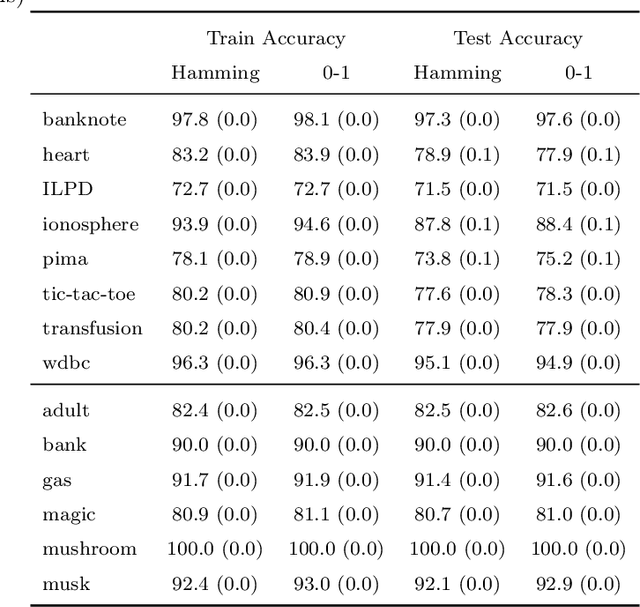
Abstract:This paper considers the learning of Boolean rules in either disjunctive normal form (DNF, OR-of-ANDs, equivalent to decision rule sets) or conjunctive normal form (CNF, AND-of-ORs) as an interpretable model for classification. An integer program is formulated to optimally trade classification accuracy for rule simplicity. We also consider the fairness setting and extend the formulation to include explicit constraints on two different measures of classification parity: equality of opportunity and equalized odds. Column generation (CG) is used to efficiently search over an exponential number of candidate clauses (conjunctions or disjunctions) without the need for heuristic rule mining. This approach also bounds the gap between the selected rule set and the best possible rule set on the training data. To handle large datasets, we propose an approximate CG algorithm using randomization. Compared to three recently proposed alternatives, the CG algorithm dominates the accuracy-simplicity trade-off in 8 out of 16 datasets. When maximized for accuracy, CG is competitive with rule learners designed for this purpose, sometimes finding significantly simpler solutions that are no less accurate. Compared to other fair and interpretable classifiers, our method is able to find rule sets that meet stricter notions of fairness with a modest trade-off in accuracy.
Fair Decision Rules for Binary Classification
Jul 03, 2021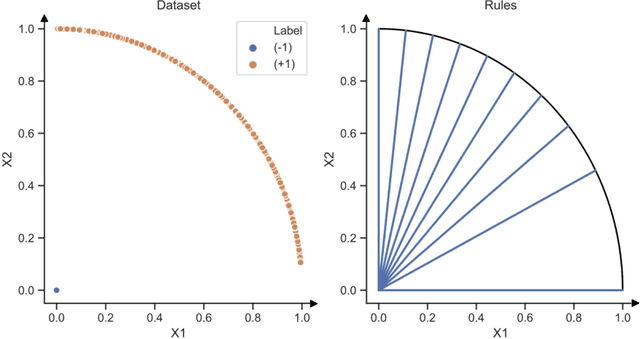


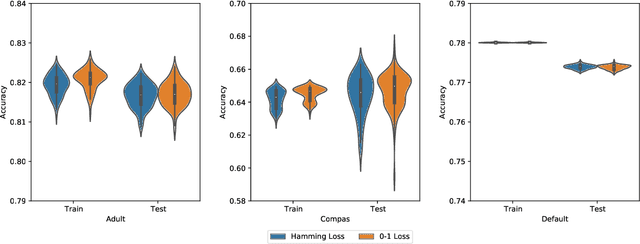
Abstract:In recent years, machine learning has begun automating decision making in fields as varied as college admissions, credit lending, and criminal sentencing. The socially sensitive nature of some of these applications together with increasing regulatory constraints has necessitated the need for algorithms that are both fair and interpretable. In this paper we consider the problem of building Boolean rule sets in disjunctive normal form (DNF), an interpretable model for binary classification, subject to fairness constraints. We formulate the problem as an integer program that maximizes classification accuracy with explicit constraints on two different measures of classification parity: equality of opportunity and equalized odds. Column generation framework, with a novel formulation, is used to efficiently search over exponentially many possible rules. When combined with faster heuristics, our method can deal with large data-sets. Compared to other fair and interpretable classifiers, our method is able to find rule sets that meet stricter notions of fairness with a modest trade-off in accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge