Probabilistic Federated Prompt-Tuning with Non-IID and Imbalanced Data

Fine-tuning pre-trained models is a popular approach in machine learning for solving complex tasks with moderate data. However, fine-tuning the entire pre-trained model is ineffective in federated data scenarios where local data distributions are diversely skewed. To address this, we explore integrating federated learning with a more effective prompt-tuning method, optimizing for a small set of input prefixes to reprogram the pre-trained model's behavior. Our approach transforms federated learning into a distributed set modeling task, aggregating diverse sets of prompts to globally fine-tune the pre-trained model. We benchmark various baselines based on direct adaptations of existing federated model aggregation techniques and introduce a new probabilistic prompt aggregation method that substantially outperforms these baselines. Our reported results on a variety of computer vision datasets confirm that the proposed method is most effective to combat extreme data heterogeneity in federated learning.

Abstracted Shapes as Tokens -- A Generalizable and Interpretable Model for Time-series Classification

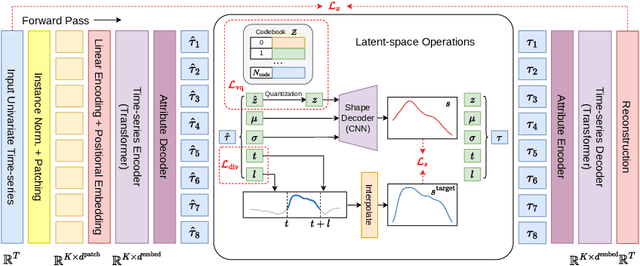
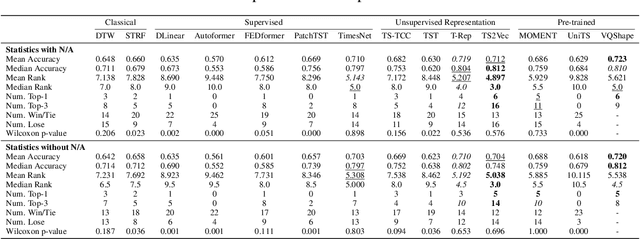
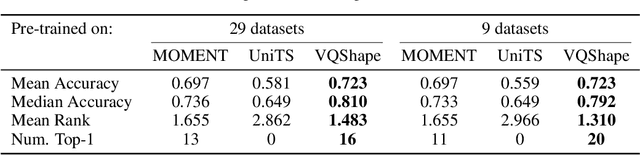
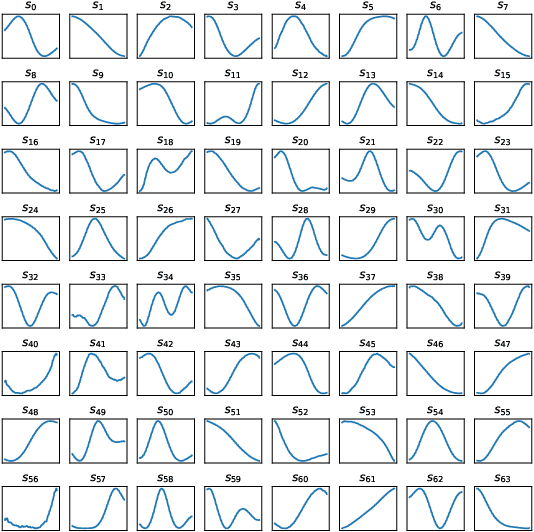
In time-series analysis, many recent works seek to provide a unified view and representation for time-series across multiple domains, leading to the development of foundation models for time-series data. Despite diverse modeling techniques, existing models are black boxes and fail to provide insights and explanations about their representations. In this paper, we present VQShape, a pre-trained, generalizable, and interpretable model for time-series representation learning and classification. By introducing a novel representation for time-series data, we forge a connection between the latent space of VQShape and shape-level features. Using vector quantization, we show that time-series from different domains can be described using a unified set of low-dimensional codes, where each code can be represented as an abstracted shape in the time domain. On classification tasks, we show that the representations of VQShape can be utilized to build interpretable classifiers, achieving comparable performance to specialist models. Additionally, in zero-shot learning, VQShape and its codebook can generalize to previously unseen datasets and domains that are not included in the pre-training process. The code and pre-trained weights are available at https://github.com/YunshiWen/VQShape.

Shuffling Gradient-Based Methods for Nonconvex-Concave Minimax Optimization

This paper aims at developing novel shuffling gradient-based methods for tackling two classes of minimax problems: nonconvex-linear and nonconvex-strongly concave settings. The first algorithm addresses the nonconvex-linear minimax model and achieves the state-of-the-art oracle complexity typically observed in nonconvex optimization. It also employs a new shuffling estimator for the "hyper-gradient", departing from standard shuffling techniques in optimization. The second method consists of two variants: semi-shuffling and full-shuffling schemes. These variants tackle the nonconvex-strongly concave minimax setting. We establish their oracle complexity bounds under standard assumptions, which, to our best knowledge, are the best-known for this specific setting. Numerical examples demonstrate the performance of our algorithms and compare them with two other methods. Our results show that the new methods achieve comparable performance with SGD, supporting the potential of incorporating shuffling strategies into minimax algorithms.

Guaranteeing Conservation Laws with Projection in Physics-Informed Neural Networks

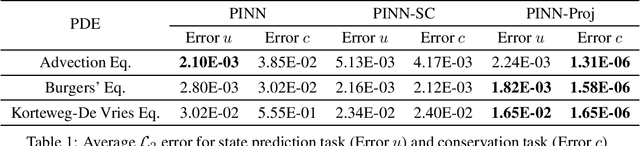
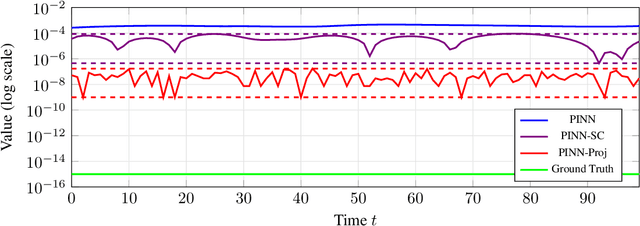
Physics-informed neural networks (PINNs) incorporate physical laws into their training to efficiently solve partial differential equations (PDEs) with minimal data. However, PINNs fail to guarantee adherence to conservation laws, which are also important to consider in modeling physical systems. To address this, we proposed PINN-Proj, a PINN-based model that uses a novel projection method to enforce conservation laws. We found that PINN-Proj substantially outperformed PINN in conserving momentum and lowered prediction error by three to four orders of magnitude from the best benchmark tested. PINN-Proj also performed marginally better in the separate task of state prediction on three PDE datasets.

TabularFM: An Open Framework For Tabular Foundational Models

Foundational models (FMs), pretrained on extensive datasets using self-supervised techniques, are capable of learning generalized patterns from large amounts of data. This reduces the need for extensive labeled datasets for each new task, saving both time and resources by leveraging the broad knowledge base established during pretraining. Most research on FMs has primarily focused on unstructured data, such as text and images, or semi-structured data, like time-series. However, there has been limited attention to structured data, such as tabular data, which, despite its prevalence, remains under-studied due to a lack of clean datasets and insufficient research on the transferability of FMs for various tabular data tasks. In response to this gap, we introduce a framework called TabularFM, which incorporates state-of-the-art methods for developing FMs specifically for tabular data. This includes variations of neural architectures such as GANs, VAEs, and Transformers. We have curated a million of tabular datasets and released cleaned versions to facilitate the development of tabular FMs. We pretrained FMs on this curated data, benchmarked various learning methods on these datasets, and released the pretrained models along with leaderboards for future comparative studies. Our fully open-sourced system provides a comprehensive analysis of the transferability of tabular FMs. By releasing these datasets, pretrained models, and leaderboards, we aim to enhance the validity and usability of tabular FMs in the near future.

Shuffling Momentum Gradient Algorithm for Convex Optimization

The Stochastic Gradient Descent method (SGD) and its stochastic variants have become methods of choice for solving finite-sum optimization problems arising from machine learning and data science thanks to their ability to handle large-scale applications and big datasets. In the last decades, researchers have made substantial effort to study the theoretical performance of SGD and its shuffling variants. However, only limited work has investigated its shuffling momentum variants, including shuffling heavy-ball momentum schemes for non-convex problems and Nesterov's momentum for convex settings. In this work, we extend the analysis of the shuffling momentum gradient method developed in [Tran et al (2021)] to both finite-sum convex and strongly convex optimization problems. We provide the first analysis of shuffling momentum-based methods for the strongly convex setting, attaining a convergence rate of $O(1/nT^2)$, where $n$ is the number of samples and $T$ is the number of training epochs. Our analysis is a state-of-the-art, matching the best rates of existing shuffling stochastic gradient algorithms in the literature.

On Partial Optimal Transport: Revising the Infeasibility of Sinkhorn and Efficient Gradient Methods

This paper studies the Partial Optimal Transport (POT) problem between two unbalanced measures with at most $n$ supports and its applications in various AI tasks such as color transfer or domain adaptation. There is hence the need for fast approximations of POT with increasingly large problem sizes in arising applications. We first theoretically and experimentally investigate the infeasibility of the state-of-the-art Sinkhorn algorithm for POT due to its incompatible rounding procedure, which consequently degrades its qualitative performance in real world applications like point-cloud registration. To this end, we propose a novel rounding algorithm for POT, and then provide a feasible Sinkhorn procedure with a revised computation complexity of $\mathcal{\widetilde O}(n^2/\varepsilon^4)$. Our rounding algorithm also permits the development of two first-order methods to approximate the POT problem. The first algorithm, Adaptive Primal-Dual Accelerated Gradient Descent (APDAGD), finds an $\varepsilon$-approximate solution to the POT problem in $\mathcal{\widetilde O}(n^{2.5}/\varepsilon)$, which is better in $\varepsilon$ than revised Sinkhorn. The second method, Dual Extrapolation, achieves the computation complexity of $\mathcal{\widetilde O}(n^2/\varepsilon)$, thereby being the best in the literature. We further demonstrate the flexibility of POT compared to standard OT as well as the practicality of our algorithms on real applications where two marginal distributions are unbalanced.

One step closer to unbiased aleatoric uncertainty estimation

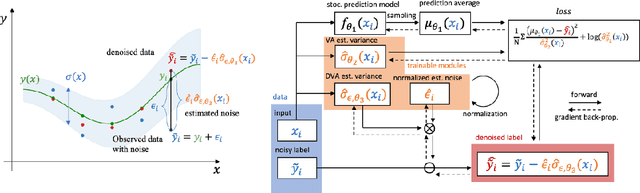
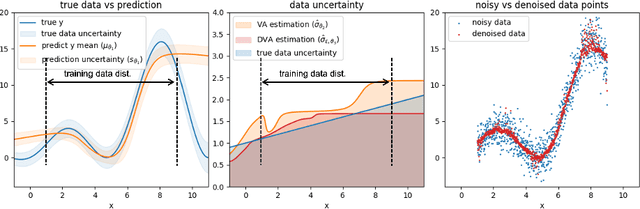
Neural networks are powerful tools in various applications, and quantifying their uncertainty is crucial for reliable decision-making. In the deep learning field, the uncertainties are usually categorized into aleatoric (data) and epistemic (model) uncertainty. In this paper, we point out that the existing popular variance attenuation method highly overestimates aleatoric uncertainty. To address this issue, we propose a new estimation method by actively de-noising the observed data. By conducting a broad range of experiments, we demonstrate that our proposed approach provides a much closer approximation to the actual data uncertainty than the standard method.

A Supervised Contrastive Learning Pretrain-Finetune Approach for Time Series

Foundation models have recently gained attention within the field of machine learning thanks to its efficiency in broad data processing. While researchers had attempted to extend this success to time series models, the main challenge is effectively extracting representations and transferring knowledge from pretraining datasets to the target finetuning dataset. To tackle this issue, we introduce a novel pretraining procedure that leverages supervised contrastive learning to distinguish features within each pretraining dataset. This pretraining phase enables a probabilistic similarity metric, which assesses the likelihood of a univariate sample being closely related to one of the pretraining datasets. Subsequently, using this similarity metric as a guide, we propose a fine-tuning procedure designed to enhance the accurate prediction of the target data by aligning it more closely with the learned dynamics of the pretraining datasets. Our experiments have shown promising results which demonstrate the efficacy of our approach.

Correlated Attention in Transformers for Multivariate Time Series

Multivariate time series (MTS) analysis prevails in real-world applications such as finance, climate science and healthcare. The various self-attention mechanisms, the backbone of the state-of-the-art Transformer-based models, efficiently discover the temporal dependencies, yet cannot well capture the intricate cross-correlation between different features of MTS data, which inherently stems from complex dynamical systems in practice. To this end, we propose a novel correlated attention mechanism, which not only efficiently captures feature-wise dependencies, but can also be seamlessly integrated within the encoder blocks of existing well-known Transformers to gain efficiency improvement. In particular, correlated attention operates across feature channels to compute cross-covariance matrices between queries and keys with different lag values, and selectively aggregate representations at the sub-series level. This architecture facilitates automated discovery and representation learning of not only instantaneous but also lagged cross-correlations, while inherently capturing time series auto-correlation. When combined with prevalent Transformer baselines, correlated attention mechanism constitutes a better alternative for encoder-only architectures, which are suitable for a wide range of tasks including imputation, anomaly detection and classification. Extensive experiments on the aforementioned tasks consistently underscore the advantages of correlated attention mechanism in enhancing base Transformer models, and demonstrate our state-of-the-art results in imputation, anomaly detection and classification.