Guaranteeing Conservation Laws with Projection in Physics-Informed Neural Networks

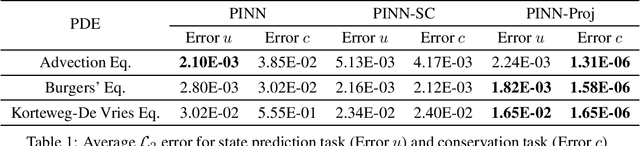
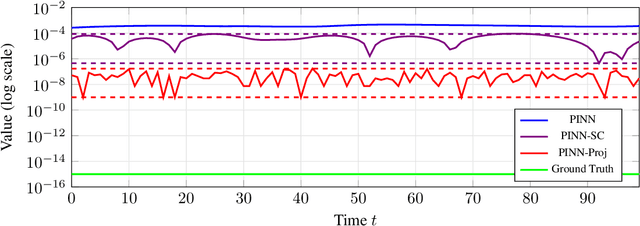
Physics-informed neural networks (PINNs) incorporate physical laws into their training to efficiently solve partial differential equations (PDEs) with minimal data. However, PINNs fail to guarantee adherence to conservation laws, which are also important to consider in modeling physical systems. To address this, we proposed PINN-Proj, a PINN-based model that uses a novel projection method to enforce conservation laws. We found that PINN-Proj substantially outperformed PINN in conserving momentum and lowered prediction error by three to four orders of magnitude from the best benchmark tested. PINN-Proj also performed marginally better in the separate task of state prediction on three PDE datasets.

Large Language Models can be Strong Self-Detoxifiers

Reducing the likelihood of generating harmful and toxic output is an essential task when aligning large language models (LLMs). Existing methods mainly rely on training an external reward model (i.e., another language model) or fine-tuning the LLM using self-generated data to influence the outcome. In this paper, we show that LLMs have the capability of self-detoxification without the use of an additional reward model or re-training. We propose \textit{Self-disciplined Autoregressive Sampling (SASA)}, a lightweight controlled decoding algorithm for toxicity reduction of LLMs. SASA leverages the contextual representations from an LLM to learn linear subspaces characterizing toxic v.s. non-toxic output in analytical forms. When auto-completing a response token-by-token, SASA dynamically tracks the margin of the current output to steer the generation away from the toxic subspace, by adjusting the autoregressive sampling strategy. Evaluated on LLMs of different scale and nature, namely Llama-3.1-Instruct (8B), Llama-2 (7B), and GPT2-L models with the RealToxicityPrompts, BOLD, and AttaQ benchmarks, SASA markedly enhances the quality of the generated sentences relative to the original models and attains comparable performance to state-of-the-art detoxification techniques, significantly reducing the toxicity level by only using the LLM's internal representations.

Deterministic fast and stable phase retrieval in multiple dimensions

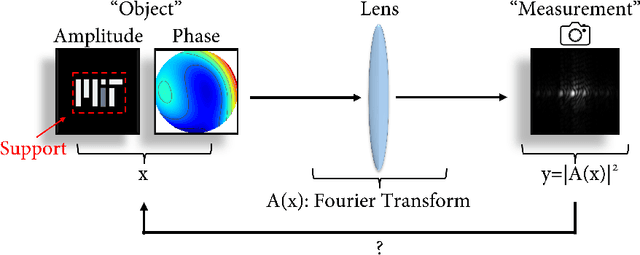
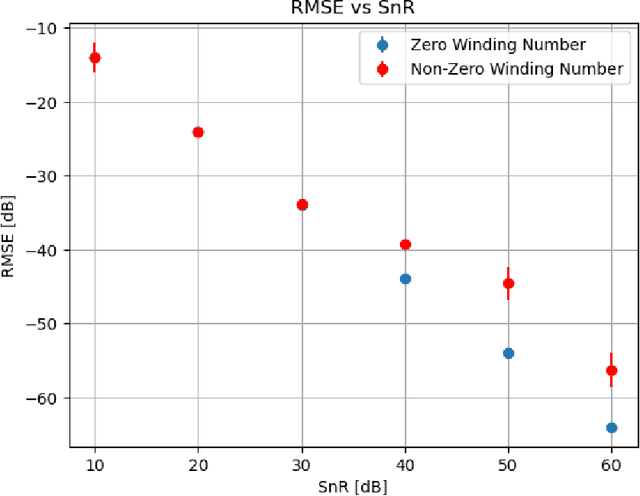
We present the first phase retrieval algorithm guaranteed to solve the multidimensional phase retrieval problem in polynomial arithmetic complexity without prior information. The method successfully terminates in O(N log(N)) operations for Fourier measurements with cardinality N. The algorithm is guaranteed to succeed for a large class of objects, which we term "Schwarz objects". We further present an easy-to-calculate and well-conditioned diagonal operator that transforms any feasible phase-retrieval instance into one that is solved by our method. We derive our method by combining techniques from classical complex analysis, algebraic topology, and modern numerical analysis. Concretely, we pose the phase retrieval problem as a multiplicative Cousin problem, construct an approximate solution using a modified integral used for the Schwarz problem, and refine the approximate solution to an exact solution via standard optimization methods. We present numerical experimentation demonstrating our algorithm's performance and its superiority to existing method. Finally, we demonstrate that our method is robust against Gaussian noise.

One step closer to unbiased aleatoric uncertainty estimation

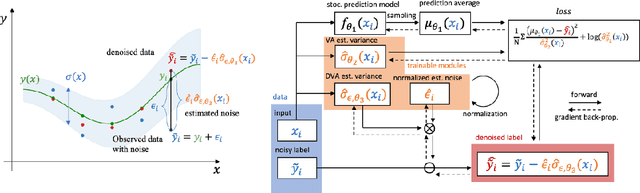
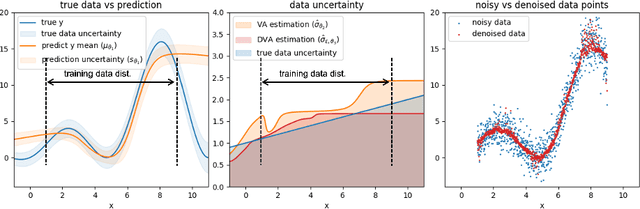
Neural networks are powerful tools in various applications, and quantifying their uncertainty is crucial for reliable decision-making. In the deep learning field, the uncertainties are usually categorized into aleatoric (data) and epistemic (model) uncertainty. In this paper, we point out that the existing popular variance attenuation method highly overestimates aleatoric uncertainty. To address this issue, we propose a new estimation method by actively de-noising the observed data. By conducting a broad range of experiments, we demonstrate that our proposed approach provides a much closer approximation to the actual data uncertainty than the standard method.

Rare Event Probability Learning by Normalizing Flows

A rare event is defined by a low probability of occurrence. Accurate estimation of such small probabilities is of utmost importance across diverse domains. Conventional Monte Carlo methods are inefficient, demanding an exorbitant number of samples to achieve reliable estimates. Inspired by the exact sampling capabilities of normalizing flows, we revisit this challenge and propose normalizing flow assisted importance sampling, termed NOFIS. NOFIS first learns a sequence of proposal distributions associated with predefined nested subset events by minimizing KL divergence losses. Next, it estimates the rare event probability by utilizing importance sampling in conjunction with the last proposal. The efficacy of our NOFIS method is substantiated through comprehensive qualitative visualizations, affirming the optimality of the learned proposal distribution, as well as a series of quantitative experiments encompassing $10$ distinct test cases, which highlight NOFIS's superiority over baseline approaches.

PIFON-EPT: MR-Based Electrical Property Tomography Using Physics-Informed Fourier Networks

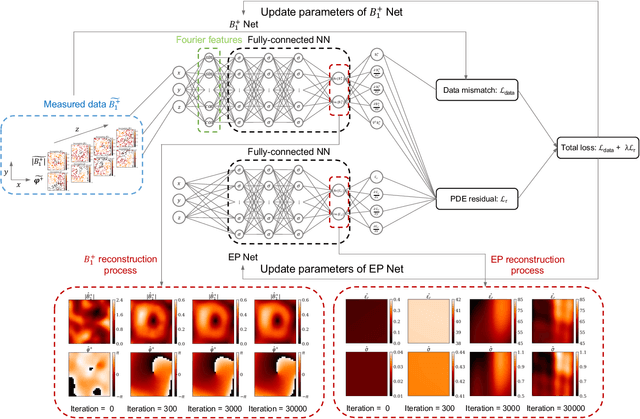
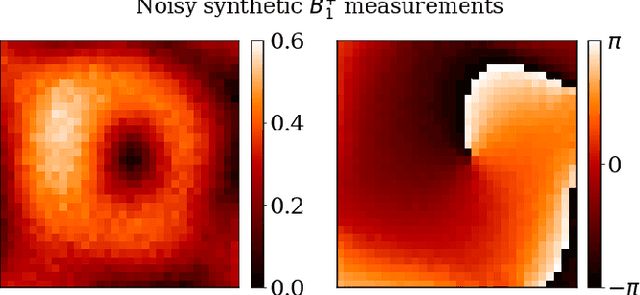
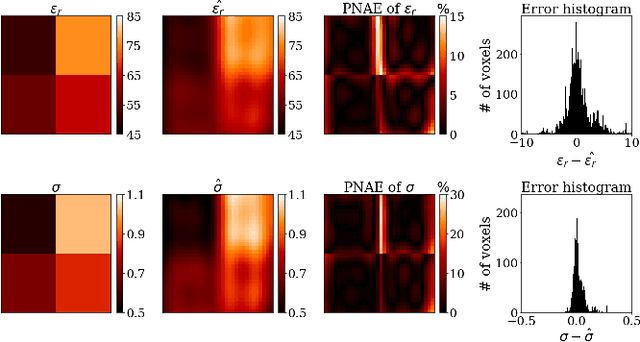
\textit{Objective:} In this paper, we introduce Physics-Informed Fourier Networks (PIFONs) for Electrical Properties (EP) Tomography (EPT). Our novel deep learning-based method is capable of learning EPs globally by solving an inverse scattering problem based on noisy and/or incomplete magnetic resonance (MR) measurements. \textit{Methods:} We use two separate fully-connected neural networks, namely $B_1^{+}$ Net and EP Net, to learn the $B_1^{+}$ field and EPs at any location. A random Fourier features mapping is embedded into $B_1^{+}$ Net, which allows it to learn the $B_1^{+}$ field more efficiently. These two neural networks are trained jointly by minimizing the combination of a physics-informed loss and a data mismatch loss via gradient descent. \textit{Results:} We showed that PIFON-EPT could provide physically consistent reconstructions of EPs and transmit field in the whole domain of interest even when half of the noisy MR measurements of the entire volume was missing. The average error was $2.49\%$, $4.09\%$ and $0.32\%$ for the relative permittivity, conductivity and $B_{1}^{+}$, respectively, over the entire volume of the phantom. In experiments that admitted a zero assumption of $B_z$, PIFON-EPT could yield accurate EP predictions near the interface between regions of different EP values without requiring any boundary conditions. \textit{Conclusion:} This work demonstrated the feasibility of PIFON-EPT, suggesting it could be an accurate and effective method for electrical properties estimation. \textit{Significance:} PIFON-EPT can efficiently de-noise MR measurements, which shows the potential to improve other MR-based EPT techniques. Furthermore, it is the first time that MR-based EPT methods can reconstruct the EPs and $B_{1}^{+}$ field simultaneously from incomplete simulated noisy MR measurements.

ConCerNet: A Contrastive Learning Based Framework for Automated Conservation Law Discovery and Trustworthy Dynamical System Prediction

Deep neural networks (DNN) have shown great capacity of modeling a dynamical system; nevertheless, they usually do not obey physics constraints such as conservation laws. This paper proposes a new learning framework named ConCerNet to improve the trustworthiness of the DNN based dynamics modeling to endow the invariant properties. ConCerNet consists of two steps: (i) a contrastive learning method to automatically capture the system invariants (i.e. conservation properties) along the trajectory observations; (ii) a neural projection layer to guarantee that the learned dynamics models preserve the learned invariants. We theoretically prove the functional relationship between the learned latent representation and the unknown system invariant function. Experiments show that our method consistently outperforms the baseline neural networks in both coordinate error and conservation metrics by a large margin. With neural network based parameterization and no dependence on prior knowledge, our method can be extended to complex and large-scale dynamics by leveraging an autoencoder.

Certified Interpretability Robustness for Class Activation Mapping

Interpreting machine learning models is challenging but crucial for ensuring the safety of deep networks in autonomous driving systems. Due to the prevalence of deep learning based perception models in autonomous vehicles, accurately interpreting their predictions is crucial. While a variety of such methods have been proposed, most are shown to lack robustness. Yet, little has been done to provide certificates for interpretability robustness. Taking a step in this direction, we present CORGI, short for Certifiably prOvable Robustness Guarantees for Interpretability mapping. CORGI is an algorithm that takes in an input image and gives a certifiable lower bound for the robustness of the top k pixels of its CAM interpretability map. We show the effectiveness of CORGI via a case study on traffic sign data, certifying lower bounds on the minimum adversarial perturbation not far from (4-5x) state-of-the-art attack methods.

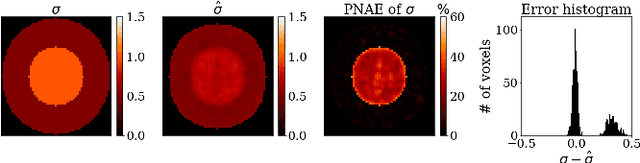
MR-Based Electrical Property Reconstruction Using Physics-Informed Neural Networks

Electrical properties (EP), namely permittivity and electric conductivity, dictate the interactions between electromagnetic waves and biological tissue. EP can be potential biomarkers for pathology characterization, such as cancer, and improve therapeutic modalities, such radiofrequency hyperthermia and ablation. MR-based electrical properties tomography (MR-EPT) uses MR measurements to reconstruct the EP maps. Using the homogeneous Helmholtz equation, EP can be directly computed through calculations of second order spatial derivatives of the measured magnetic transmit or receive fields $(B_{1}^{+}, B_{1}^{-})$. However, the numerical approximation of derivatives leads to noise amplifications in the measurements and thus erroneous reconstructions. Recently, a noise-robust supervised learning-based method (DL-EPT) was introduced for EP reconstruction. However, the pattern-matching nature of such network does not allow it to generalize for new samples since the network's training is done on a limited number of simulated data. In this work, we leverage recent developments on physics-informed deep learning to solve the Helmholtz equation for the EP reconstruction. We develop deep neural network (NN) algorithms that are constrained by the Helmholtz equation to effectively de-noise the $B_{1}^{+}$ measurements and reconstruct EP directly at an arbitrarily high spatial resolution without requiring any known $B_{1}^{+}$ and EP distribution pairs.

SynBench: Task-Agnostic Benchmarking of Pretrained Representations using Synthetic Data

Recent success in fine-tuning large models, that are pretrained on broad data at scale, on downstream tasks has led to a significant paradigm shift in deep learning, from task-centric model design to task-agnostic representation learning and task-specific fine-tuning. As the representations of pretrained models are used as a foundation for different downstream tasks, this paper proposes a new task-agnostic framework, \textit{SynBench}, to measure the quality of pretrained representations using synthetic data. We set up a reference by a theoretically-derived robustness-accuracy tradeoff of the class conditional Gaussian mixture. Given a pretrained model, the representations of data synthesized from the Gaussian mixture are used to compare with our reference to infer the quality. By comparing the ratio of area-under-curve between the raw data and their representations, SynBench offers a quantifiable score for robustness-accuracy performance benchmarking. Our framework applies to a wide range of pretrained models taking continuous data inputs and is independent of the downstream tasks and datasets. Evaluated with several pretrained vision transformer models, the experimental results show that our SynBench score well matches the actual linear probing performance of the pre-trained model when fine-tuned on downstream tasks. Moreover, our framework can be used to inform the design of robust linear probing on pretrained representations to mitigate the robustness-accuracy tradeoff in downstream tasks.