Separable Operator Networks

Operator learning has become a powerful tool in machine learning for modeling complex physical systems. Although Deep Operator Networks (DeepONet) show promise, they require extensive data acquisition. Physics-informed DeepONets (PI-DeepONet) mitigate data scarcity but suffer from inefficient training processes. We introduce Separable Operator Networks (SepONet), a novel framework that significantly enhances the efficiency of physics-informed operator learning. SepONet uses independent trunk networks to learn basis functions separately for different coordinate axes, enabling faster and more memory-efficient training via forward-mode automatic differentiation. We provide theoretical guarantees for SepONet using the universal approximation theorem and validate its performance through comprehensive benchmarking against PI-DeepONet. Our results demonstrate that for the 1D time-dependent advection equation, when targeting a mean relative $\ell_{2}$ error of less than 6% on 100 unseen variable coefficients, SepONet provides up to $112 \times$ training speed-up and $82 \times$ GPU memory usage reduction compared to PI-DeepONet. Similar computational advantages are observed across various partial differential equations, with SepONet's efficiency gains scaling favorably as problem complexity increases. This work paves the way for extreme-scale learning of continuous mappings between infinite-dimensional function spaces.

Real-Time FJ/MAC PDE Solvers via Tensorized, Back-Propagation-Free Optical PINN Training

Solving partial differential equations (PDEs) numerically often requires huge computing time, energy cost, and hardware resources in practical applications. This has limited their applications in many scenarios (e.g., autonomous systems, supersonic flows) that have a limited energy budget and require near real-time response. Leveraging optical computing, this paper develops an on-chip training framework for physics-informed neural networks (PINNs), aiming to solve high-dimensional PDEs with fJ/MAC photonic power consumption and ultra-low latency. Despite the ultra-high speed of optical neural networks, training a PINN on an optical chip is hard due to (1) the large size of photonic devices, and (2) the lack of scalable optical memory devices to store the intermediate results of back-propagation (BP). To enable realistic optical PINN training, this paper presents a scalable method to avoid the BP process. We also employ a tensor-compressed approach to improve the convergence and scalability of our optical PINN training. This training framework is designed with tensorized optical neural networks (TONN) for scalable inference acceleration and MZI phase-domain tuning for \textit{in-situ} optimization. Our simulation results of a 20-dim HJB PDE show that our photonic accelerator can reduce the number of MZIs by a factor of $1.17\times 10^3$, with only $1.36$ J and $1.15$ s to solve this equation. This is the first real-size optical PINN training framework that can be applied to solve high-dimensional PDEs.

Tensor-Compressed Back-Propagation-Free Training for (Physics-Informed) Neural Networks

Backward propagation (BP) is widely used to compute the gradients in neural network training. However, it is hard to implement BP on edge devices due to the lack of hardware and software resources to support automatic differentiation. This has tremendously increased the design complexity and time-to-market of on-device training accelerators. This paper presents a completely BP-free framework that only requires forward propagation to train realistic neural networks. Our technical contributions are three-fold. Firstly, we present a tensor-compressed variance reduction approach to greatly improve the scalability of zeroth-order (ZO) optimization, making it feasible to handle a network size that is beyond the capability of previous ZO approaches. Secondly, we present a hybrid gradient evaluation approach to improve the efficiency of ZO training. Finally, we extend our BP-free training framework to physics-informed neural networks (PINNs) by proposing a sparse-grid approach to estimate the derivatives in the loss function without using BP. Our BP-free training only loses little accuracy on the MNIST dataset compared with standard first-order training. We also demonstrate successful results in training a PINN for solving a 20-dim Hamiltonian-Jacobi-Bellman PDE. This memory-efficient and BP-free approach may serve as a foundation for the near-future on-device training on many resource-constraint platforms (e.g., FPGA, ASIC, micro-controllers, and photonic chips).

DeepOHeat: Operator Learning-based Ultra-fast Thermal Simulation in 3D-IC Design

Thermal issue is a major concern in 3D integrated circuit (IC) design. Thermal optimization of 3D IC often requires massive expensive PDE simulations. Neural network-based thermal prediction models can perform real-time prediction for many unseen new designs. However, existing works either solve 2D temperature fields only or do not generalize well to new designs with unseen design configurations (e.g., heat sources and boundary conditions). In this paper, for the first time, we propose DeepOHeat, a physics-aware operator learning framework to predict the temperature field of a family of heat equations with multiple parametric or non-parametric design configurations. This framework learns a functional map from the function space of multiple key PDE configurations (e.g., boundary conditions, power maps, heat transfer coefficients) to the function space of the corresponding solution (i.e., temperature fields), enabling fast thermal analysis and optimization by changing key design configurations (rather than just some parameters). We test DeepOHeat on some industrial design cases and compare it against Celsius 3D from Cadence Design Systems. Our results show that, for the unseen testing cases, a well-trained DeepOHeat can produce accurate results with $1000\times$ to $300000\times$ speedup.

PIFON-EPT: MR-Based Electrical Property Tomography Using Physics-Informed Fourier Networks

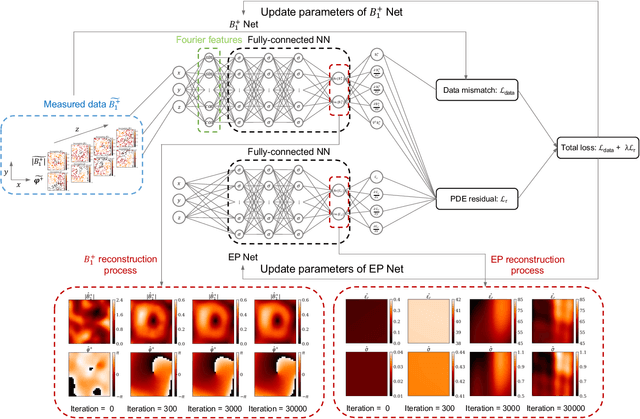
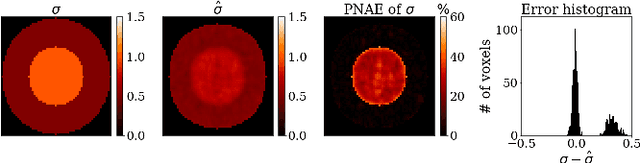
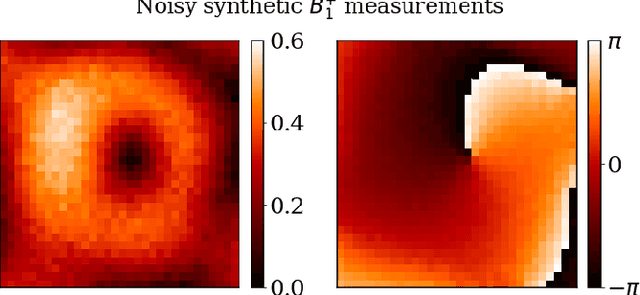
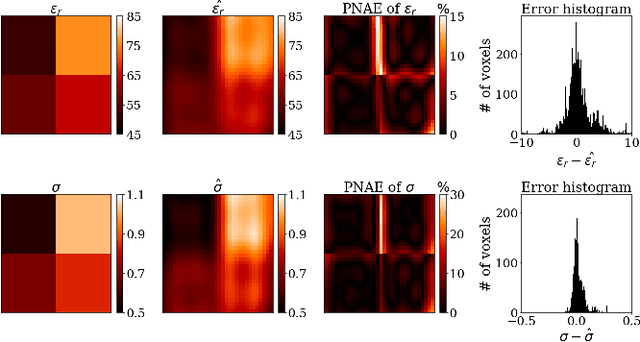
\textit{Objective:} In this paper, we introduce Physics-Informed Fourier Networks (PIFONs) for Electrical Properties (EP) Tomography (EPT). Our novel deep learning-based method is capable of learning EPs globally by solving an inverse scattering problem based on noisy and/or incomplete magnetic resonance (MR) measurements. \textit{Methods:} We use two separate fully-connected neural networks, namely $B_1^{+}$ Net and EP Net, to learn the $B_1^{+}$ field and EPs at any location. A random Fourier features mapping is embedded into $B_1^{+}$ Net, which allows it to learn the $B_1^{+}$ field more efficiently. These two neural networks are trained jointly by minimizing the combination of a physics-informed loss and a data mismatch loss via gradient descent. \textit{Results:} We showed that PIFON-EPT could provide physically consistent reconstructions of EPs and transmit field in the whole domain of interest even when half of the noisy MR measurements of the entire volume was missing. The average error was $2.49\%$, $4.09\%$ and $0.32\%$ for the relative permittivity, conductivity and $B_{1}^{+}$, respectively, over the entire volume of the phantom. In experiments that admitted a zero assumption of $B_z$, PIFON-EPT could yield accurate EP predictions near the interface between regions of different EP values without requiring any boundary conditions. \textit{Conclusion:} This work demonstrated the feasibility of PIFON-EPT, suggesting it could be an accurate and effective method for electrical properties estimation. \textit{Significance:} PIFON-EPT can efficiently de-noise MR measurements, which shows the potential to improve other MR-based EPT techniques. Furthermore, it is the first time that MR-based EPT methods can reconstruct the EPs and $B_{1}^{+}$ field simultaneously from incomplete simulated noisy MR measurements.

MR-Based Electrical Property Reconstruction Using Physics-Informed Neural Networks

Electrical properties (EP), namely permittivity and electric conductivity, dictate the interactions between electromagnetic waves and biological tissue. EP can be potential biomarkers for pathology characterization, such as cancer, and improve therapeutic modalities, such radiofrequency hyperthermia and ablation. MR-based electrical properties tomography (MR-EPT) uses MR measurements to reconstruct the EP maps. Using the homogeneous Helmholtz equation, EP can be directly computed through calculations of second order spatial derivatives of the measured magnetic transmit or receive fields $(B_{1}^{+}, B_{1}^{-})$. However, the numerical approximation of derivatives leads to noise amplifications in the measurements and thus erroneous reconstructions. Recently, a noise-robust supervised learning-based method (DL-EPT) was introduced for EP reconstruction. However, the pattern-matching nature of such network does not allow it to generalize for new samples since the network's training is done on a limited number of simulated data. In this work, we leverage recent developments on physics-informed deep learning to solve the Helmholtz equation for the EP reconstruction. We develop deep neural network (NN) algorithms that are constrained by the Helmholtz equation to effectively de-noise the $B_{1}^{+}$ measurements and reconstruct EP directly at an arbitrarily high spatial resolution without requiring any known $B_{1}^{+}$ and EP distribution pairs.

TT-PINN: A Tensor-Compressed Neural PDE Solver for Edge Computing

Physics-informed neural networks (PINNs) have been increasingly employed due to their capability of modeling complex physics systems. To achieve better expressiveness, increasingly larger network sizes are required in many problems. This has caused challenges when we need to train PINNs on edge devices with limited memory, computing and energy resources. To enable training PINNs on edge devices, this paper proposes an end-to-end compressed PINN based on Tensor-Train decomposition. In solving a Helmholtz equation, our proposed model significantly outperforms the original PINNs with few parameters and achieves satisfactory prediction with up to 15$\times$ overall parameter reduction.

When and why PINNs fail to train: A neural tangent kernel perspective

Physics-informed neural networks (PINNs) have lately received great attention thanks to their flexibility in tackling a wide range of forward and inverse problems involving partial differential equations. However, despite their noticeable empirical success, little is known about how such constrained neural networks behave during their training via gradient descent. More importantly, even less is known about why such models sometimes fail to train at all. In this work, we aim to investigate these questions through the lens of the Neural Tangent Kernel (NTK); a kernel that captures the behavior of fully-connected neural networks in the infinite width limit during training via gradient descent. Specifically, we derive the NTK of PINNs and prove that, under appropriate conditions, it converges to a deterministic kernel that stays constant during training in the infinite-width limit. This allows us to analyze the training dynamics of PINNs through the lens of their limiting NTK and find a remarkable discrepancy in the convergence rate of the different loss components contributing to the total training error. To address this fundamental pathology, we propose a novel gradient descent algorithm that utilizes the eigenvalues of the NTK to adaptively calibrate the convergence rate of the total training error. Finally, we perform a series of numerical experiments to verify the correctness of our theory and the practical effectiveness of the proposed algorithms. The data and code accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/PINNsNTK}.