Scalable Back-Propagation-Free Training of Optical Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have shown promise in solving partial differential equations (PDEs), with growing interest in their energy-efficient, real-time training on edge devices. Photonic computing offers a potential solution to achieve this goal because of its ultra-high operation speed. However, the lack of photonic memory and the large device sizes prevent training real-size PINNs on photonic chips. This paper proposes a completely back-propagation-free (BP-free) and highly salable framework for training real-size PINNs on silicon photonic platforms. Our approach involves three key innovations: (1) a sparse-grid Stein derivative estimator to avoid the BP in the loss evaluation of a PINN, (2) a dimension-reduced zeroth-order optimization via tensor-train decomposition to achieve better scalability and convergence in BP-free training, and (3) a scalable on-chip photonic PINN training accelerator design using photonic tensor cores. We validate our numerical methods on both low- and high-dimensional PDE benchmarks. Through circuit simulation based on real device parameters, we further demonstrate the significant performance benefit (e.g., real-time training, huge chip area reduction) of our photonic accelerator.

Experimental Demonstration of an Optical Neural PDE Solver via On-Chip PINN Training

Partial differential equation (PDE) is an important math tool in science and engineering. This paper experimentally demonstrates an optical neural PDE solver by leveraging the back-propagation-free on-photonic-chip training of physics-informed neural networks.

Real-Time FJ/MAC PDE Solvers via Tensorized, Back-Propagation-Free Optical PINN Training

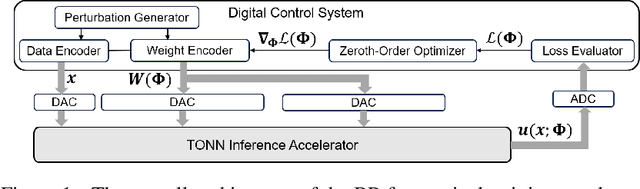
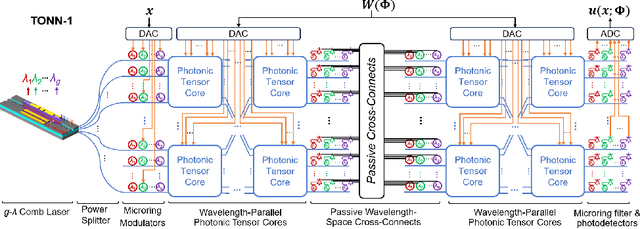
Solving partial differential equations (PDEs) numerically often requires huge computing time, energy cost, and hardware resources in practical applications. This has limited their applications in many scenarios (e.g., autonomous systems, supersonic flows) that have a limited energy budget and require near real-time response. Leveraging optical computing, this paper develops an on-chip training framework for physics-informed neural networks (PINNs), aiming to solve high-dimensional PDEs with fJ/MAC photonic power consumption and ultra-low latency. Despite the ultra-high speed of optical neural networks, training a PINN on an optical chip is hard due to (1) the large size of photonic devices, and (2) the lack of scalable optical memory devices to store the intermediate results of back-propagation (BP). To enable realistic optical PINN training, this paper presents a scalable method to avoid the BP process. We also employ a tensor-compressed approach to improve the convergence and scalability of our optical PINN training. This training framework is designed with tensorized optical neural networks (TONN) for scalable inference acceleration and MZI phase-domain tuning for \textit{in-situ} optimization. Our simulation results of a 20-dim HJB PDE show that our photonic accelerator can reduce the number of MZIs by a factor of $1.17\times 10^3$, with only $1.36$ J and $1.15$ s to solve this equation. This is the first real-size optical PINN training framework that can be applied to solve high-dimensional PDEs.

High-Speed and Energy-Efficient Non-Volatile Silicon Photonic Memory Based on Heterogeneously Integrated Memresonator

Recently, interest in programmable photonics integrated circuits has grown as a potential hardware framework for deep neural networks, quantum computing, and field programmable arrays (FPGAs). However, these circuits are constrained by the limited tuning speed and large power consumption of the phase shifters used. In this paper, introduced for the first time are memresonators, or memristors heterogeneously integrated with silicon photonic microring resonators, as phase shifters with non-volatile memory. These devices are capable of retention times of 12 hours, switching voltages lower than 5 V, an endurance of 1,000 switching cycles. Also, these memresonators have been switched using voltage pulses as short as 300 ps with a record low switching energy of 0.15 pJ. Furthermore, these memresonators are fabricated on a heterogeneous III-V/Si platform capable of integrating a rich family of active, passive, and non-linear optoelectronic devices, such as lasers and detectors, directly on-chip to enable in-memory photonic computing and further advance the scalability of integrated photonic processor circuits.

Tensorized Optical Multimodal Fusion Network

We propose the first tensorized optical multimodal fusion network architecture with a self-attention mechanism and low-rank tensor fusion. Simulation results show $51.3 \times$ less hardware requirement and $3.7\times 10^{13}$ MAC/J energy efficiency.

Inverse Design of Grating Couplers Using the Policy Gradient Method from Reinforcement Learning

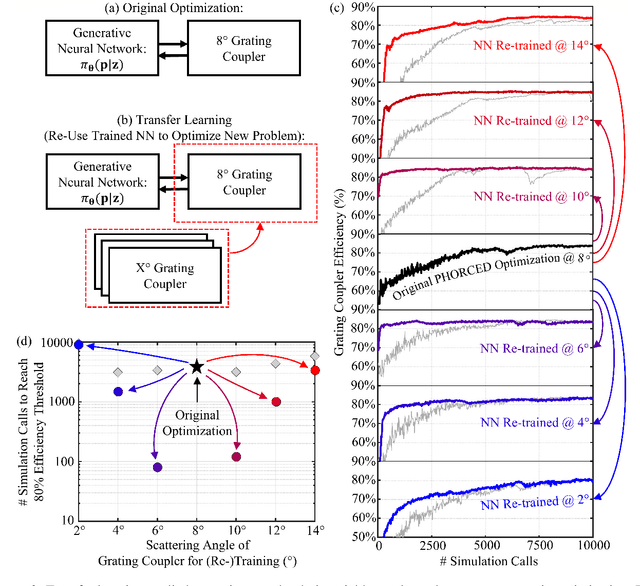
We present a proof-of-concept technique for the inverse design of electromagnetic devices motivated by the policy gradient method in reinforcement learning, named PHORCED (PHotonic Optimization using REINFORCE Criteria for Enhanced Design). This technique uses a probabilistic generative neural network interfaced with an electromagnetic solver to assist in the design of photonic devices, such as grating couplers. We show that PHORCED obtains better performing grating coupler designs than local gradient-based inverse design via the adjoint method, while potentially providing faster convergence over competing state-of-the-art generative methods. Furthermore, we implement transfer learning with PHORCED, demonstrating that a neural network trained to optimize 8$^\circ$ grating couplers can then be re-trained on grating couplers with alternate scattering angles while requiring >$10\times$ fewer simulations than control cases.