TEON: Tensorized Orthonormalization Beyond Layer-Wise Muon for Large Language Model Pre-Training

The Muon optimizer has demonstrated strong empirical performance in pre-training large language models by performing matrix-level gradient (or momentum) orthogonalization in each layer independently. In this work, we propose TEON, a principled generalization of Muon that extends orthogonalization beyond individual layers by modeling the gradients of a neural network as a structured higher-order tensor. We present TEON's improved convergence guarantee over layer-wise Muon, and further develop a practical instantiation of TEON based on the theoretical analysis with corresponding ablation. We evaluate our approach on two widely adopted architectures: GPT-style models, ranging from 130M to 774M parameters, and LLaMA-style models, ranging from 60M to 1B parameters. Experimental results show that TEON consistently improves training and validation perplexity across model scales and exhibits strong robustness under various approximate SVD schemes.

BOOST: BOttleneck-Optimized Scalable Training Framework for Low-Rank Large Language Models

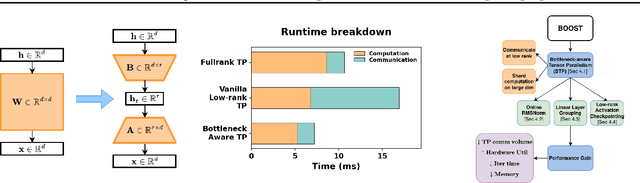
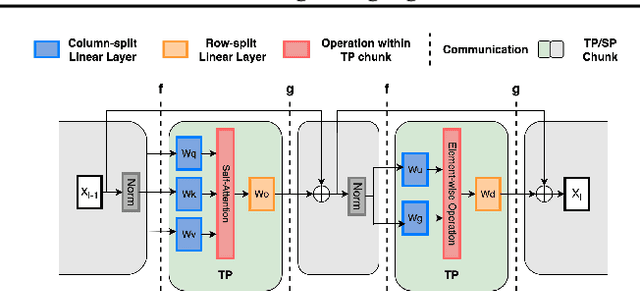
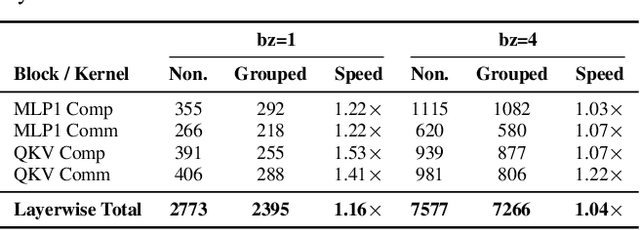
The scale of transformer model pre-training is constrained by the increasing computation and communication cost. Low-rank bottleneck architectures offer a promising solution to significantly reduce the training time and memory footprint with minimum impact on accuracy. Despite algorithmic efficiency, bottleneck architectures scale poorly under standard tensor parallelism. Simply applying 3D parallelism designed for full-rank methods leads to excessive communication and poor GPU utilization. To address this limitation, we propose BOOST, an efficient training framework tailored for large-scale low-rank bottleneck architectures. BOOST introduces a novel Bottleneck-aware Tensor Parallelism, and combines optimizations such as online-RMSNorm, linear layer grouping, and low-rank activation checkpointing to achieve end-to-end training speedup. Evaluations on different low-rank bottleneck architectures demonstrate that BOOST achieves 1.46-1.91$\times$ speedup over full-rank model baselines and 1.87-2.27$\times$ speedup over low-rank model with naively integrated 3D parallelism, with improved GPU utilization and reduced communication overhead.

LOTS of Fashion! Multi-Conditioning for Image Generation via Sketch-Text Pairing

Fashion design is a complex creative process that blends visual and textual expressions. Designers convey ideas through sketches, which define spatial structure and design elements, and textual descriptions, capturing material, texture, and stylistic details. In this paper, we present LOcalized Text and Sketch for fashion image generation (LOTS), an approach for compositional sketch-text based generation of complete fashion outlooks. LOTS leverages a global description with paired localized sketch + text information for conditioning and introduces a novel step-based merging strategy for diffusion adaptation. First, a Modularized Pair-Centric representation encodes sketches and text into a shared latent space while preserving independent localized features; then, a Diffusion Pair Guidance phase integrates both local and global conditioning via attention-based guidance within the diffusion model's multi-step denoising process. To validate our method, we build on Fashionpedia to release Sketchy, the first fashion dataset where multiple text-sketch pairs are provided per image. Quantitative results show LOTS achieves state-of-the-art image generation performance on both global and localized metrics, while qualitative examples and a human evaluation study highlight its unprecedented level of design customization.

Evaluating Attribute Confusion in Fashion Text-to-Image Generation

Despite the rapid advances in Text-to-Image (T2I) generation models, their evaluation remains challenging in domains like fashion, involving complex compositional generation. Recent automated T2I evaluation methods leverage pre-trained vision-language models to measure cross-modal alignment. However, our preliminary study reveals that they are still limited in assessing rich entity-attribute semantics, facing challenges in attribute confusion, i.e., when attributes are correctly depicted but associated to the wrong entities. To address this, we build on a Visual Question Answering (VQA) localization strategy targeting one single entity at a time across both visual and textual modalities. We propose a localized human evaluation protocol and introduce a novel automatic metric, Localized VQAScore (L-VQAScore), that combines visual localization with VQA probing both correct (reflection) and miss-localized (leakage) attribute generation. On a newly curated dataset featuring challenging compositional alignment scenarios, L-VQAScore outperforms state-of-the-art T2I evaluation methods in terms of correlation with human judgments, demonstrating its strength in capturing fine-grained entity-attribute associations. We believe L-VQAScore can be a reliable and scalable alternative to subjective evaluations.

Fluid Aerial Networks: UAV Rotation for Inter-Cell Interference Mitigation

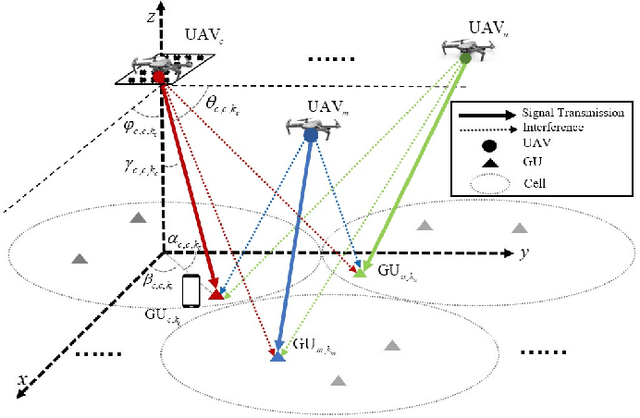
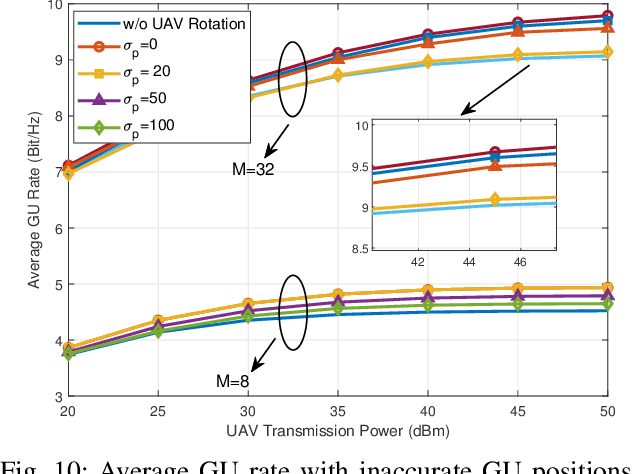
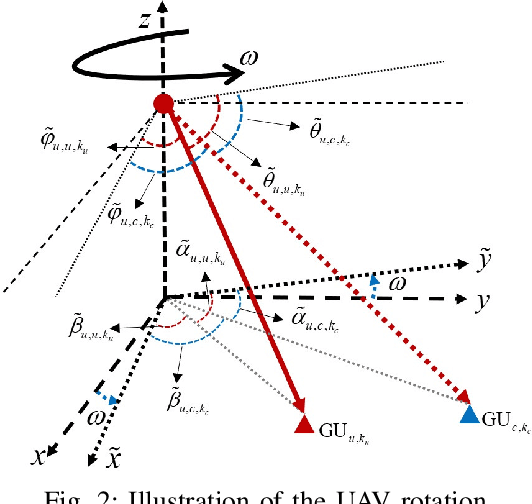
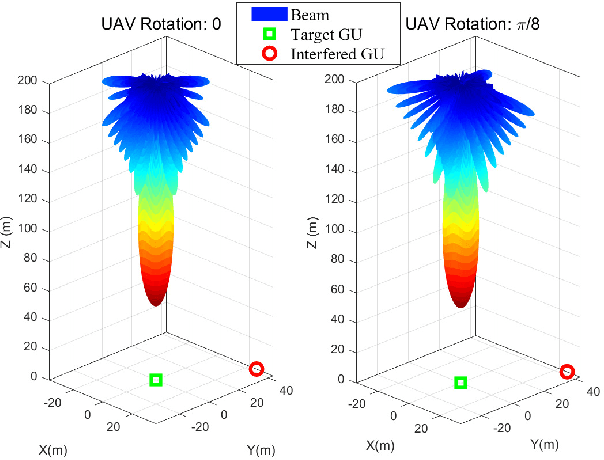
With the rapid development of aerial infrastructure, unmanned aerial vehicles (UAVs) that function as aerial base stations (ABSs) extend terrestrial network services into the sky, enabling on-demand connectivity and enhancing emergency communication capabilities in cellular networks by leveraging the flexibility and mobility of UAVs. In such a UAV-assisted network, this paper investigates position-based beamforming between ABSs and ground users (GUs). To mitigate inter-cell interference, we propose a novel fluid aerial network that leverages ABS rotation to increase multi-cell capacity and overall network efficiency. Specifically, considering the line-of-sight channel model, the spatial beamforming weights are determined by the orientation angles of the GUs. In this direction, we examine the beamforming gain of a two-dimensional multiple-input multiple-output (MIMO) array at various ground positions, revealing that ABS rotation significantly affects multi-user channel correlation and inter-cell interference. Based on these findings, we propose an alternative low-complexity algorithm to design the optimal rotation angle for ABSs, aiming to reduce inter-cell interference and thus maximize the sum rate of multi-cell systems. In simulations, exhaustive search serves as a benchmark to validate the optimization performance of the proposed sequential ABS rotation scheme. Moreover, simulation results demonstrate that, in interference-limited regions, the proposed ABS rotation paradigm can significantly reduce inter-cell interference in terrestrial networks and improve the multi-cell sum rate by approximately 10\% compared to fixed-direction ABSs without rotation.

LaX: Boosting Low-Rank Training of Foundation Models via Latent Crossing

Training foundation models such as ViTs and LLMs requires tremendous computing cost. Low-rank matrix or tensor factorization offers a parameter-efficient alternative, but often downgrades performance due to the restricted parameter space. In this work, we introduce {\textbf{Latent Crossing (LaX)}} -- a simple yet effective plug-and-play module that enhances the capacity of low-rank models by enabling information flow across low-rank subspaces. We extensively validate the benefits of LaX on pre-training tasks with ViT-Base/Large and LLaMA-like models ranging from 60M to 1B parameters. LaX boosts low-rank model performance to match or exceed the full-rank baselines while using 2-3\(\times\) fewer parameters. When equipped with low-rank adapters (i.e., LoRA) for fine-tuning LLaMA-7/13B, LaX consistently improves performance on arithmetic and common sense reasoning tasks with negligible cost.

Seeing the Abstract: Translating the Abstract Language for Vision Language Models

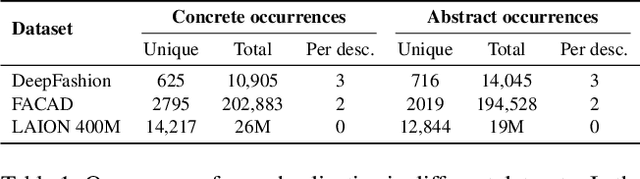
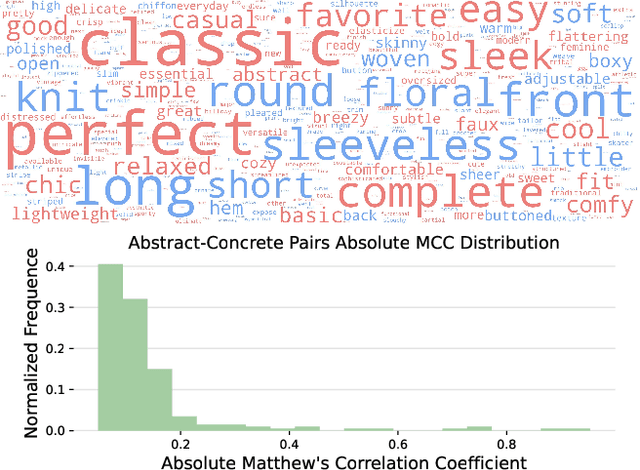
Natural language goes beyond dryly describing visual content. It contains rich abstract concepts to express feeling, creativity and properties that cannot be directly perceived. Yet, current research in Vision Language Models (VLMs) has not shed light on abstract-oriented language. Our research breaks new ground by uncovering its wide presence and under-estimated value, with extensive analysis. Particularly, we focus our investigation on the fashion domain, a highly-representative field with abstract expressions. By analyzing recent large-scale multimodal fashion datasets, we find that abstract terms have a dominant presence, rivaling the concrete ones, providing novel information, and being useful in the retrieval task. However, a critical challenge emerges: current general-purpose or fashion-specific VLMs are pre-trained with databases that lack sufficient abstract words in their text corpora, thus hindering their ability to effectively represent abstract-oriented language. We propose a training-free and model-agnostic method, Abstract-to-Concrete Translator (ACT), to shift abstract representations towards well-represented concrete ones in the VLM latent space, using pre-trained models and existing multimodal databases. On the text-to-image retrieval task, despite being training-free, ACT outperforms the fine-tuned VLMs in both same- and cross-dataset settings, exhibiting its effectiveness with a strong generalization capability. Moreover, the improvement introduced by ACT is consistent with various VLMs, making it a plug-and-play solution.

Parameter-Efficient Continual Fine-Tuning: A Survey

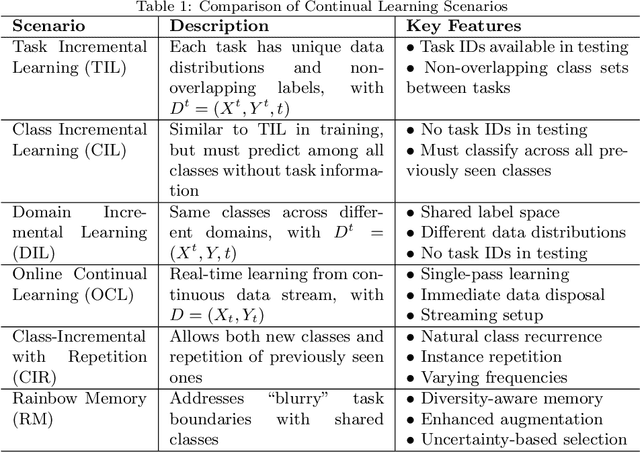
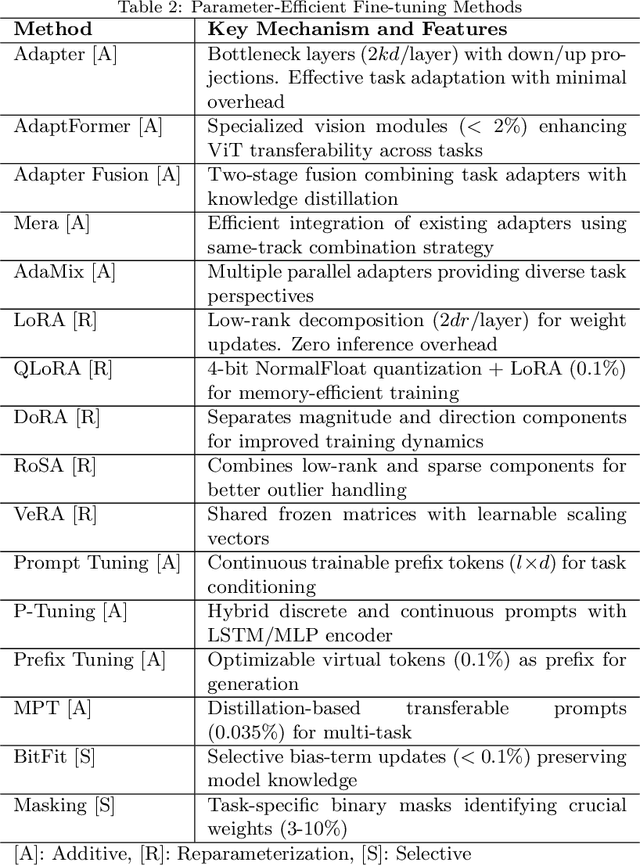
The emergence of large pre-trained networks has revolutionized the AI field, unlocking new possibilities and achieving unprecedented performance. However, these models inherit a fundamental limitation from traditional Machine Learning approaches: their strong dependence on the \textit{i.i.d.} assumption hinders their adaptability to dynamic learning scenarios. We believe the next breakthrough in AI lies in enabling efficient adaptation to evolving environments -- such as the real world -- where new data and tasks arrive sequentially. This challenge defines the field of Continual Learning (CL), a Machine Learning paradigm focused on developing lifelong learning neural models. One alternative to efficiently adapt these large-scale models is known Parameter-Efficient Fine-Tuning (PEFT). These methods tackle the issue of adapting the model to a particular data or scenario by performing small and efficient modifications, achieving similar performance to full fine-tuning. However, these techniques still lack the ability to adjust the model to multiple tasks continually, as they suffer from the issue of Catastrophic Forgetting. In this survey, we first provide an overview of CL algorithms and PEFT methods before reviewing the state-of-the-art on Parameter-Efficient Continual Fine-Tuning (PECFT). We examine various approaches, discuss evaluation metrics, and explore potential future research directions. Our goal is to highlight the synergy between CL and Parameter-Efficient Fine-Tuning, guide researchers in this field, and pave the way for novel future research directions.

DeepOHeat-v1: Efficient Operator Learning for Fast and Trustworthy Thermal Simulation and Optimization in 3D-IC Design

Thermal analysis is crucial in three-dimensional integrated circuit (3D-IC) design due to increased power density and complex heat dissipation paths. Although operator learning frameworks such as DeepOHeat have demonstrated promising preliminary results in accelerating thermal simulation, they face critical limitations in prediction capability for multi-scale thermal patterns, training efficiency, and trustworthiness of results during design optimization. This paper presents DeepOHeat-v1, an enhanced physics-informed operator learning framework that addresses these challenges through three key innovations. First, we integrate Kolmogorov-Arnold Networks with learnable activation functions as trunk networks, enabling an adaptive representation of multi-scale thermal patterns. This approach achieves a $1.25\times$ and $6.29\times$ reduction in error in two representative test cases. Second, we introduce a separable training method that decomposes the basis function along the coordinate axes, achieving $62\times$ training speedup and $31\times$ GPU memory reduction in our baseline case, and enabling thermal analysis at resolutions previously infeasible due to GPU memory constraints. Third, we propose a confidence score to evaluate the trustworthiness of the predicted results, and further develop a hybrid optimization workflow that combines operator learning with finite difference (FD) using Generalized Minimal Residual (GMRES) method for incremental solution refinement, enabling efficient and trustworthy thermal optimization. Experimental results demonstrate that DeepOHeat-v1 achieves accuracy comparable to optimization using high-fidelity finite difference solvers, while speeding up the entire optimization process by $70.6\times$ in our test cases, effectively minimizing the peak temperature through optimal placement of heat-generating components.

QuZO: Quantized Zeroth-Order Fine-Tuning for Large Language Models

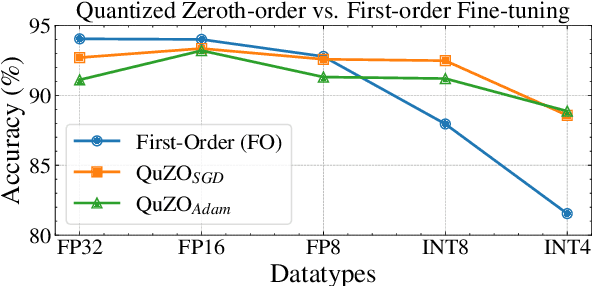
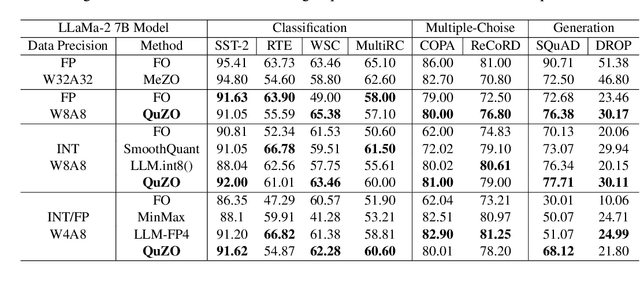
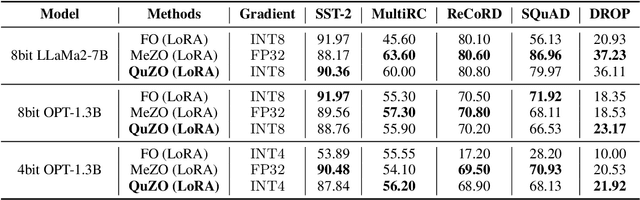
Language Models (LLMs) are often quantized to lower precision to reduce the memory cost and latency in inference. However, quantization often degrades model performance, thus fine-tuning is required for various down-stream tasks. Traditional fine-tuning methods such as stochastic gradient descent and Adam optimization require backpropagation, which are error-prone in the low-precision settings. To overcome these limitations, we propose the Quantized Zeroth-Order (QuZO) framework, specifically designed for fine-tuning LLMs through low-precision (e.g., 4- or 8-bit) forward passes. Our method can avoid the error-prone low-precision straight-through estimator, and utilizes optimized stochastic rounding to mitigate the increased bias. QuZO simplifies the training process, while achieving results comparable to first-order methods in ${\rm FP}8$ and superior accuracy in ${\rm INT}8$ and ${\rm INT}4$ training. Experiments demonstrate that low-bit training QuZO achieves performance comparable to MeZO optimization on GLUE, Multi-Choice, and Generation tasks, while reducing memory cost by $2.94 \times$ in LLaMA2-7B fine-tuning compared to quantized first-order methods.