Separable Operator Networks

Operator learning has become a powerful tool in machine learning for modeling complex physical systems. Although Deep Operator Networks (DeepONet) show promise, they require extensive data acquisition. Physics-informed DeepONets (PI-DeepONet) mitigate data scarcity but suffer from inefficient training processes. We introduce Separable Operator Networks (SepONet), a novel framework that significantly enhances the efficiency of physics-informed operator learning. SepONet uses independent trunk networks to learn basis functions separately for different coordinate axes, enabling faster and more memory-efficient training via forward-mode automatic differentiation. We provide theoretical guarantees for SepONet using the universal approximation theorem and validate its performance through comprehensive benchmarking against PI-DeepONet. Our results demonstrate that for the 1D time-dependent advection equation, when targeting a mean relative $\ell_{2}$ error of less than 6% on 100 unseen variable coefficients, SepONet provides up to $112 \times$ training speed-up and $82 \times$ GPU memory usage reduction compared to PI-DeepONet. Similar computational advantages are observed across various partial differential equations, with SepONet's efficiency gains scaling favorably as problem complexity increases. This work paves the way for extreme-scale learning of continuous mappings between infinite-dimensional function spaces.

Inverse Design of Grating Couplers Using the Policy Gradient Method from Reinforcement Learning

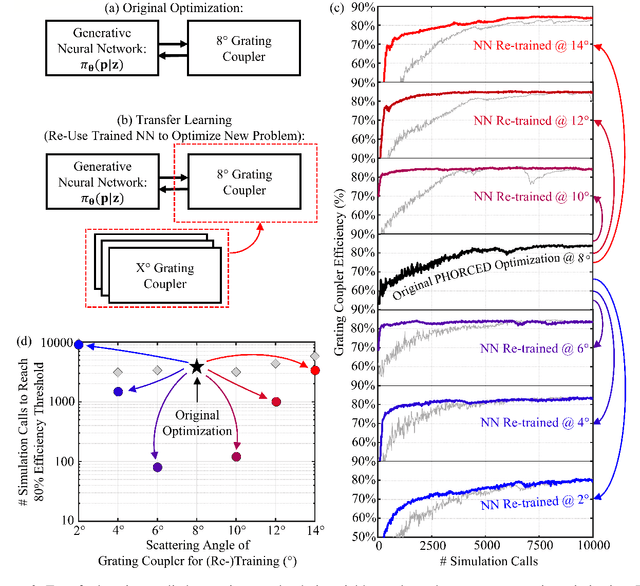
We present a proof-of-concept technique for the inverse design of electromagnetic devices motivated by the policy gradient method in reinforcement learning, named PHORCED (PHotonic Optimization using REINFORCE Criteria for Enhanced Design). This technique uses a probabilistic generative neural network interfaced with an electromagnetic solver to assist in the design of photonic devices, such as grating couplers. We show that PHORCED obtains better performing grating coupler designs than local gradient-based inverse design via the adjoint method, while potentially providing faster convergence over competing state-of-the-art generative methods. Furthermore, we implement transfer learning with PHORCED, demonstrating that a neural network trained to optimize 8$^\circ$ grating couplers can then be re-trained on grating couplers with alternate scattering angles while requiring >$10\times$ fewer simulations than control cases.